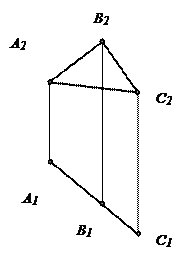
Проецирование прямого угла

При пересечении двух прямых образуются углы, которые проецируются на любую плоскость проекций без искажений в случае, если обе прямые лежат в плоскости, параллельной плоскости проекций. Если две прямые пересекаются под прямым углом, то следует знать, что проецирование прямого угла имеет особое свойство.

Если одна из сторон прямого угла параллельна одной из плоскостей проекций, то прямой угол проецируется на эту плоскость без искажений (инвариантные свойства параллельного проецирования).

На комплексном чертеже (рисунок 14 а, б, в) показаны проекции взаимно перпендикулярных прямых, где а, б, с – прямые общего положения; h – горизонталь, f – фронталь, р – профильная прямая уровня.

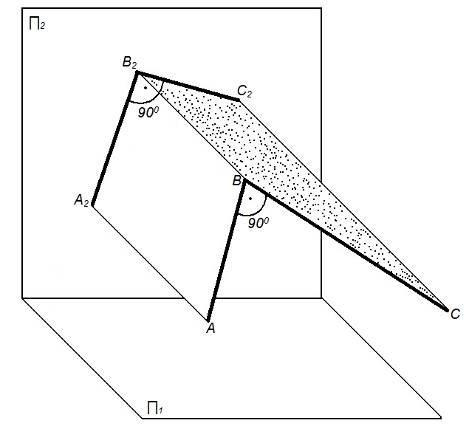
Рисунок 13 – Проецирование прямого угла

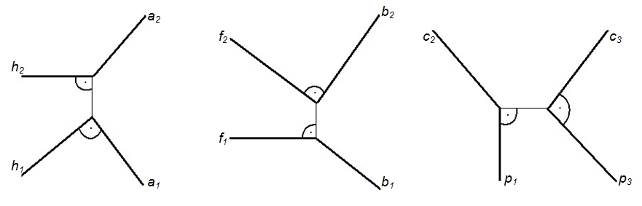
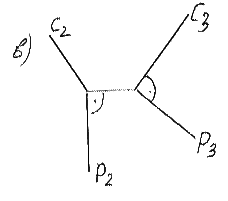
а) б) в)

Рисунок 14 – Комплексный чертеж взаимно перпендикулярных прямых

Плоскость

Проекцией любой плоскости является геометрическое место проекций всех ее точек. Если рассматривать плоскость, расположенную не перпендикулярно и не параллельно ни одной из плоскостей проекций, то ее проекции целиком заполнят собой поля плоскостей П₁, П₂, П₃. Поэтому на комплексном чертеже задаются лишь некоторые геометрические элементы, определяющее положение заданной плоскости в пространстве (таблица 1):.

Таблица 1 – Способы задания плоскости

Задание плоскости	Наглядное изображение	Комплексный чертеж
Тремя точками, не лежащими на одной прямой
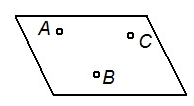
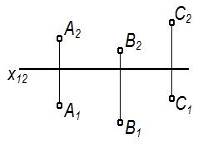
Прямой и точкой, не принадлежащей прямой
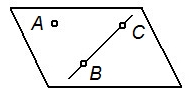
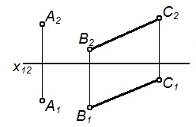
Двумя параллельными прямыми
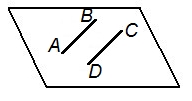
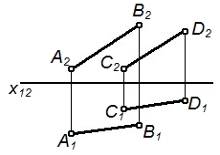
Двумя пересекающимися прямыми
Плоской фигурой

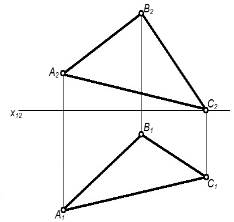
Возможны следующие положения плоскости относительно плоскостей проекции:

1) плоскость не перпендикулярна и не параллельна ни к одной плоскости проекций – общего положения (рисунок 15);

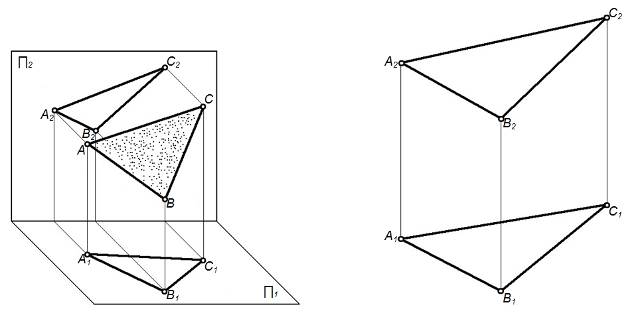
Рисунок 15 – Плоскость общего положения

2) плоскость перпендикулярна к какой-либо плоскости проекций - проецирующая (рисунок 16);

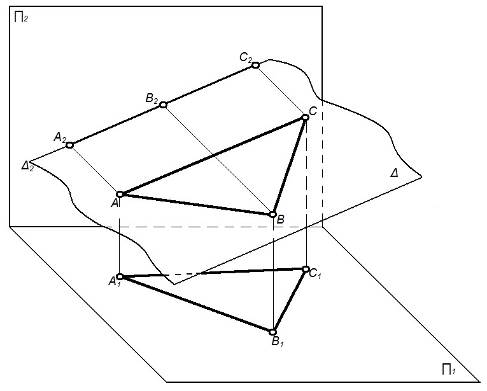
Рисунок 16 – Проецирующая плоскость

3) плоскость параллельна какой-либо плоскости проекций (дважды проецирующая) – плоскость уровня (рисунок 17).

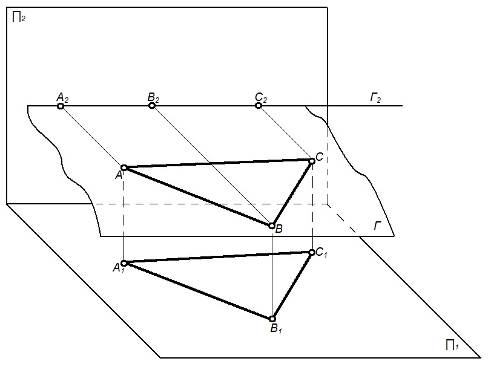
Рисунок 17 – Плоскость уровня

На комплексном чертеже рассматривается три проецирующих плоскости и три плоскости уровня (таблица 2).

Таблица 2 – Частные случаи расположения плоскостей

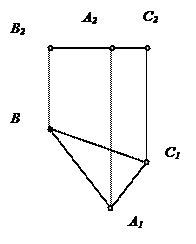
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ
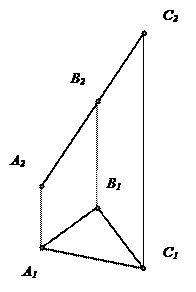
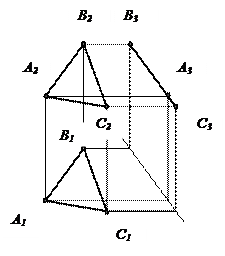
Горизонтально-проецирующая плоскость	Фронтально-проецирующая плоскость	Профильно-проецирующая плоскость
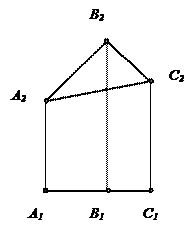
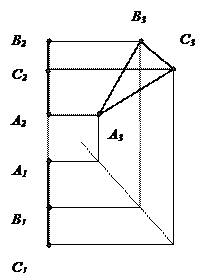
ПЛОСКОСТИ УРОВНЯ
Горизонтальная плоскость уровня	Фронтальная плоскость уровня	Профильная плоскость уровня

Горизонтально проецирующая плоскость - ^П₁. Горизонтальная проекция такой плоскости вырождается в прямую линию (главная проекция). Это главный признак горизонтально проецирующей плоскости на комплексном чертеже. Главная проекция плоскости обладает собирательными свойствами, т.е. проекции всех точек принадлежащих горизонтально проецирующей плоскости на П₁ совпадают с главной проекцией этой плоскости.

Фронтально проецирующая плоскость - ^П₂. Фронтальная проекция такой плоскости вырождается в прямую линию (главная прямая). Это признак фронтально проецирующей на комплексном чертеже. Главная проекция (проекция на П₂) обладает собирательным свойством, т.е. проекции всех точек, принадлежащих фронтально проецирующей плоскости на П₂ совпадают с главной проекцией этой плоскости.

Профильно проецирующая плоскость - ^П₃. Профильная проекция такой плоскости вырождается в прямую линию (главная проекция). Это признак профильно проецирующей плоскости на комплексном чертеже. Главная проекция обладает собирательным свойством.

Горизонтальная плоскость уровня параллельна П₁, одновременно такая плоскость является профильно и фронтально проецирующей.

Фронтальная плоскость уровня параллельна П₂, одновременно горизонтально и профильно проецирующая плоскость.

Профильная плоскость уровня параллельна П₃, одновременно горизонтально и фронтально проецирующая плоскость.