Колебания упругих стержней
| Для простоты будем считать, что масса стержня намного меньше массы груза, поэтому силами инерции элементов стержня пренебрегаем. Колебания подразделяются на свободные и вынужденные. Свободные колебания возникают после кратковременного приложения внешней силы. Вынужденные колебания вызываются переменами во времени нагрузками | 
рис.20.6.
|
20.5.1. Свободные колебания
Приложим кратковременную нагрузку и удалим ее. Поскольку внешних сил нет, то колебания существуют по причине наличия сил инерции.
Рассмотрим сечение I-I.
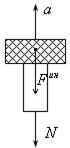
рис.20.7
На него действует сила растяжения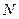 
. Если груз движется с некоторым ускорением 
, то на груз действует сила инерции
.
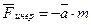Запишем условие равенства нулю всех сил.
.
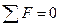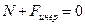. (20.10)
Выразим 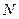и Fинер через удлинение стержня. Имеем закон Гука:
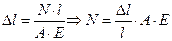. (20.11)
С другой стороны перемещение u груза это и есть величина удлинения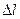 
. Из теоретической механики известно, что ускорение и Fинер вычисляются по формуле:
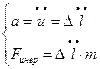(20.12)
Подставим в (20.10):
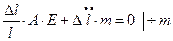
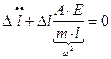
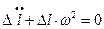
Здесь обозначено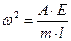 
.
Решение этого уравнения, которое называется уравнением свободных колебаний, имеет вид (это легко проверить путем подстановки)
.
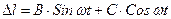рис.20.8
Коэффициент 
характеризует то, насколько часто повторяется волна синусоиды в каком-либо интервале. Чем больше , тем чаще повторяется волна синусоиды, поэтому называют частотой свободных колебаний стержне. Например, на рисунке справа волн больше, значит для нее больше.
Константы B и С определяются из начальных условий, например, если при t=0 оттянуть стержень на величину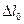 
, а затем отпустить, то имеем следующие начальные условия:
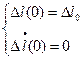
Подставим в эти условия наше решение:
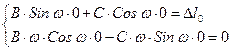
Получим:
.
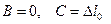Таким образом:
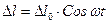
рис.20.9
Примечание: величина является наиболее важной характеристикой сооружения, поскольку она определяет возможность появления резонанса от воздействия внешних нагрузок.
Дата добавления: 2015-11-28; просмотров: 657;