Касательные напряжения в балке

Впервые формулу для τ_zy вывел Журавский Д. И. в 1855 году.

Рассмотрим поперечный изгиб (рис. 15.9, как и ранее для удобства записи индексы для напряжений σ_z , τ_zy в дальнейшем будем опускать).

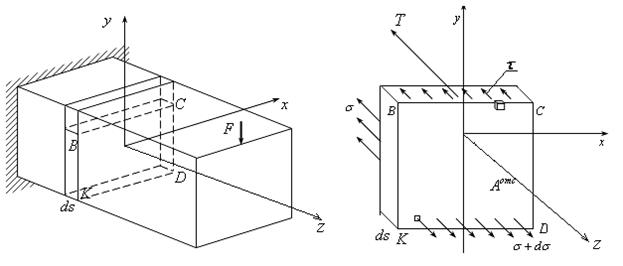
рис. 15.9 рис. 15.10

Вырежем тонкий диск шириной ds. Из него еще раз вырежем часть диска с площадью сечения А^отс = BCDK (рис. 15.9, 15.10).

Верхняя часть диска воздействует на нижнюю часть касательными напряжениями 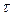(рис. 15.10).

Найдем это из уравнения равновесия диска BCDK. Запишем уравнение:

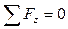(15.13)

Поскольку 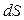бесконечно мал, то можно считать, что на верхней площадке диска . Тогда равнодействующая напряжений 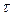на этой верхней площадке будет:

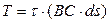(15.14)

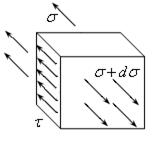
Теперь подсчитаем силы, которые действуют в направлении оси z на переднюю и заднюю площадки нашего усеченного диска. На них действуют нормальные напряжения. На заднюю действуют 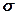(рис.15.10). На переднюю действуют нормальные напряжения, которые мало отличаются от 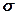. Как обычно эту фразу записываем так: на переднюю площадку действуют . Так же, как обычно площадь BCDK разбиваем на малые площади 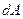и находим силы, которые на них действуют. Это будут 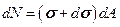. Суммируя эти силы получим, что на площадь BCDK спереди действует сила

(15.15)

На такую же площадь нашего диска, но сзади действует сила:

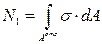(15.16)

Уравнение (15.13) примет вид:

.

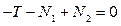Подставляя сюда соотношения (15.14)-(15.16) получим:

Отсюда:

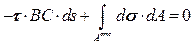
Деля на ВСds получим:

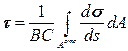(15.17)

По формуле Навье (15.8) имеем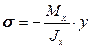

Отсюда:

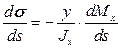(15.18)

Согласно уравнению равновесия (3.2) элемента балки имеем:

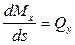(15.19)

Таким образом:

Обозначая ВС через b полученную формулу Журавского запишем в виде:

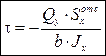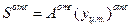, (15.20)

Перечислим использованные обозначения.

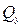- поперечная сила;

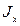- момент инерции всего сечения;

b - ширина сечения на уровне того микроэлемента, в котором вычисляется 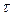(если фигура не прямоугольник, то ширина b будетразная на разных уровнях рассматриваемого микроэлемента);

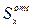- статический момент отсеченной площади А^отс - части площадисечения, которая лежит ниже рассматриваемого малого элемента (т.е. фигуры BCDK), , в котором вычисляется ;

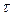(у_ц.т.)^отс - координата центра тяжести отсеченной площади BCDK.

15.6. Касательные напряжения в полке двутавра

Как и ранее, вырежем из балки диск шириной (рис. 15.12), а из него затем с помощью вертикального сечения I-I вырежем часть полки (рис. 15.13). Обозначим через BC расстояние от левого конца полки до сечения I-I На эту часть полки спереди и сзади действуют растягивающие напряжения, мало отличающиеся друг от друга, а именно, отличающиеся на величину .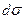

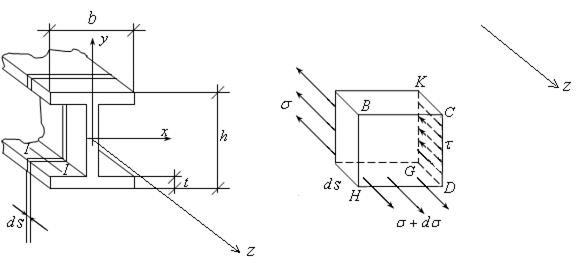
рис. 15.12 рис. 15.13

Некомпенсированное воздействие 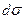должно чем-то уравновешиваться. Этими силами могут быть только касательные напряжения, которые воздействуют на правое сечение KCDG этого элемента

Запишем уравнение равновесия:

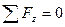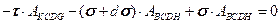: (15.21)

В отличие от предыдущего раздела здесь не интегрируем по площади BCDH, так как толщина полок t мала, поэтому можно считать, что по высоте полки. Кроме того, ввиду малости t можно считать что 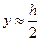. Тогда получим из (15.21):

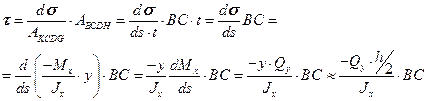(15.22)

Таким образом: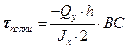

Видно, что 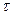прямо пропорционально BC, то есть зависит от BC линейно (BC – расстояние от левого конца полки до сечения I-I). Следовательно:

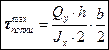(15.23)

Для правой полки распределение напряжений аналогично рис.15.13. и имеет вид, приведенный на рис. 15.14. Поэтому формула для 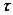получится такая же как (15.23). Однако здесь направление нормали к сечению противоположно оси x, поэтому 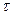будет иметь противоположный знак.

Эпюра 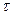примет вид, приведенный на рис. 15.15.

рис.15.14. рис.15.15

Следствия. Как видно из формул (15.20), (15.23), касательные напряжения возникают только там где поперечная сила Q_y отлична от нуля.