Теории кратковременной прочности
Исторически наиболее популярными были пять теорий прочности. Однако некоторые из них плохо подтверждаются экспериментом, поэтому на сегодня не применяются или применяются лишь в частных случаях.
Если в теле ненулевыми являются, например, только 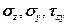 , а остальные напряжения равны нулю, то говорят, что тело находиться в плоском напряженном состоянии. В общем случае напряженное состояние называют трехосным. Ниже для простоты рассмотрим, в основном, лишь плоское напряженное состояние, поскольку в строительных сооружениях оно имеет место в подавляющем большинстве случаев.
, а остальные напряжения равны нулю, то говорят, что тело находиться в плоском напряженном состоянии. В общем случае напряженное состояние называют трехосным. Ниже для простоты рассмотрим, в основном, лишь плоское напряженное состояние, поскольку в строительных сооружениях оно имеет место в подавляющем большинстве случаев.
Вырежем из тела малый элемент с гранями, параллельными главным площадкам. Так как 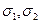 - главные, то касательных напряжений нет.
- главные, то касательных напряжений нет.
Рис.11.11
Основная проблема, которая обсуждается в теориях прочности, заключается в следующем.
Пусть известен предел прочности 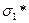 при одноосном нагружении элемента только напряжением
при одноосном нагружении элемента только напряжением 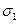 (см. рис.11.11). Вопрос – увеличится, уменьшится или не изменится прочность элемента, если предварительно нагрузить его в поперечном направлении напряжением
(см. рис.11.11). Вопрос – увеличится, уменьшится или не изменится прочность элемента, если предварительно нагрузить его в поперечном направлении напряжением 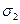 ? Другими словами, какое значение напряжения
? Другими словами, какое значение напряжения 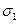 потребуется для того, чтобы разрушить образец - меньшее, чем
потребуется для того, чтобы разрушить образец - меньшее, чем 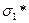 , большее, чем
, большее, чем 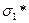 , или же равное
, или же равное 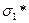 ? Оказалось, что однозначного ответа на этот вопрос нет, так как для различных классов материалов степень влияния
? Оказалось, что однозначного ответа на этот вопрос нет, так как для различных классов материалов степень влияния 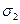 разная, причем
разная, причем 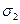 может как повышать прочность, так и понижать ее, а иногда на прочность в направлении действия
может как повышать прочность, так и понижать ее, а иногда на прочность в направлении действия 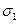 оно никак не влияет.
оно никак не влияет.
Введем понятие предельной кривой, с помощью которой ответ на этот вопрос можно получить графически.
Проведем ряд экспериментов при разных комбинациях 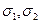 и доведем образец до разрушения. Сведем результаты в таблицу, например в виде:
и доведем образец до разрушения. Сведем результаты в таблицу, например в виде:
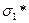 МПа МПа
| -210 | … | ||
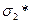 МПа МПа
| -170 | … |
Отложим эти значения в системе координат 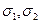 (рис.11.12)
(рис.11.12)
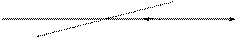
Рис.11.12
Получим ряд точек. Соединяя их, получим некоторую кривую замкнутой формы, которая называется предельной кривой.
Смысл предельной кривой в том, что если комбинации 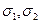 образуют точку внутри кривой, то разрушения не происходит, а если проектные
образуют точку внутри кривой, то разрушения не происходит, а если проектные 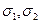 окажутся на кривой или вне нее, то материал не выдержит эту комбинацию напряжений. Ниже рассмотрим различные случаи предельных кривых.
окажутся на кривой или вне нее, то материал не выдержит эту комбинацию напряжений. Ниже рассмотрим различные случаи предельных кривых.
Примечание: так как осуществить многоосное нагружение достаточно трудно, то для построения кривой часто применяли различные соображения.
Дата добавления: 2015-11-28; просмотров: 694;
