Закон сохранения импульса. II закон Ньютона

Вектор, равный произведению массы m материальной точки на ее скорость 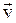, называется импульсом материальной точки:

. (1.17)

Импульс системы из N материальных точек равен геометрической сумме импульсов всех материальных точек, входящих в систему:

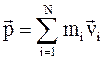. (1.18)

Для замкнутой системы материальных точек полный импульс не меняется с течением времени: 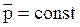- закон сохранения импульса.

Для количественной характеристики воздействия одного тела на другое в динамике вводится понятие силы. Сила – количественная мера взаимодействия тел.

II закон Ньютона: винерциальной системе отсчета производная от импульса материальной точки по времени равна действующей на нее силе:

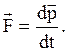(1.19)

В рамках классической механики действует закон сохранения массы, согласно которому масса тела не зависит от скорости движения материальной точки. Тогда уравнение (1.19) перепишем следующим образом:

.

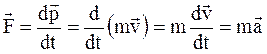Итак, в рамках классической механики II закон Ньютона запишется в виде:

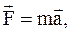(1.20)

т.е. произведение массы материальной точки на ее ускорение равно действующей на точку силе. Уравнения (1.19) и (1.20) называются уравнениями движения материальной точки.

III закон Ньютона

Рассмотрим замкнутую систему, состоящую из двух частиц, взаимодействующих с силами 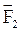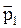и ; и 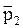- импульсы этих частиц.

Для замкнутой системы справедлив закон сохранения импульса:

.

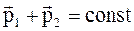Дифференцируя это соотношение по времени:

,

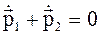на основании (1.19) получим:

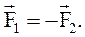(1.21)

III закон Ньютона: две взаимодействующие материальные точки действуют друг на друга с силами, равными по величине и противоположными по направлению.

Как и II закон, III закон Ньютона выполняется только в инерциальных системах отсчета.