Скорость материальной точки
Пусть при движении по криволинейной траектории материальная точка в некоторый момент времени t1 занимала положение A с радиус-вектором 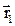 , а в момент времени t2=t1+Dt – положение B с радиус-вектором
, а в момент времени t2=t1+Dt – положение B с радиус-вектором 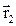 (рис.1.1).
(рис.1.1).
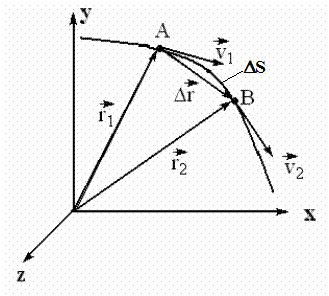
Рис. 1.1. Траектория движения материальной точки
За время Dt=t2-t1 радиус-вектор получил приращение 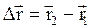 .
.
Перемещением 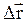 называется вектор, соединяющий начальное положение частицы и ее конечное положение.
называется вектор, соединяющий начальное положение частицы и ее конечное положение.
Расстояние DS, пройденное частицей вдоль траектории за рассматриваемый промежуток времени, называется длиной пути ÈAB=DS.
Средней векторной скоростью материальной точки называют отношение приращения радиус-вектора точки к тому промежутку времени, за который это приращение произошло:
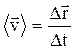 . (1.1)
. (1.1)
Из (1.1) видно, что вектор скорости сонаправлен с вектором перемещения.
Средняя путевая скорость
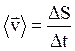 .
.
Если 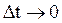 , то отношение
, то отношение 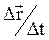 стремится к некоторому пределу, называемому скоростью материальной точки в момент времени t или мгновенной скоростью
стремится к некоторому пределу, называемому скоростью материальной точки в момент времени t или мгновенной скоростью 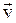 :
:
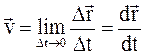 . (1.2)
. (1.2)
Мгновенной скоростью точки называют вектор, численно равный первой производной по времени от радиус-вектора, определяющего положение этой точки в данный момент времени.
Модуль мгновенной скорости:
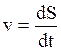 .
.
Знак d обозначает бесконечно малое изменение физической величины. Знак D обозначает конечное изменение физической величины. Из рис.1.1 видно, что за время Dt модуль перемещения меньше пути: 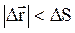 . При Dt®0, т.е. за элементарный промежуток времени dt, разницей между модулем перемещения и длиной пути можно пренебречь:
. При Dt®0, т.е. за элементарный промежуток времени dt, разницей между модулем перемещения и длиной пути можно пренебречь: 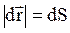 .
.
Вектор 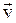 направлен по касательной к траектории в этой точке, т.е.
направлен по касательной к траектории в этой точке, т.е.
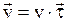 , (1.3)
, (1.3)
где 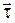 - единичный вектор касательной к траектории в данной точке;
- единичный вектор касательной к траектории в данной точке;
v– модуль скорости, равный:
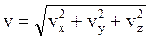 .
.
Дата добавления: 2016-01-07; просмотров: 703;
