Система сходящихся сил
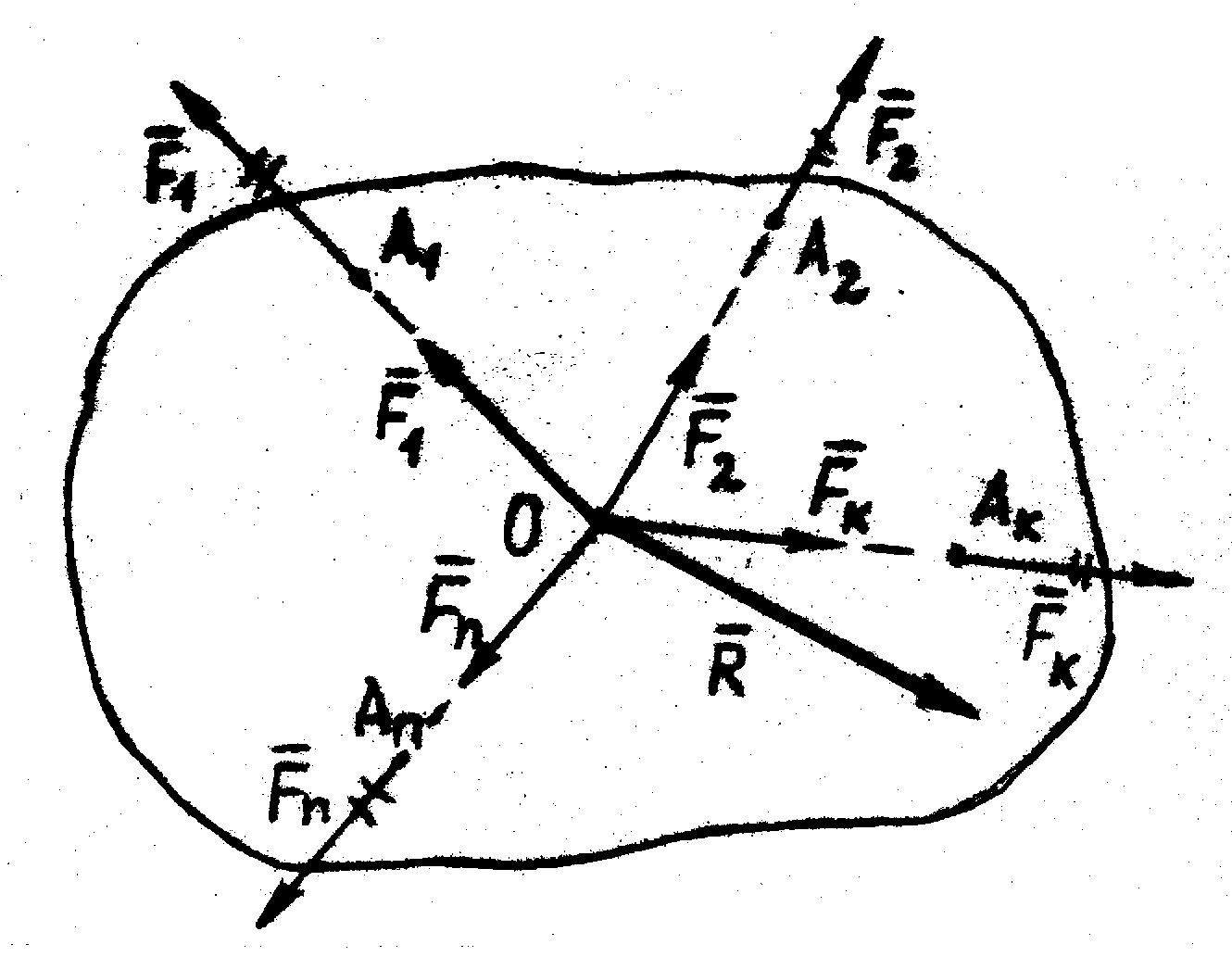
Сходящейся называется такая система сил, в которой линии действия всех сил пересекаются в одной точке (например, в точке О на рис. 15).
| Рис. 15 |
На тело действует пространственная система сходящихся сил 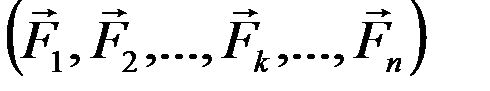 . Силы приложены соответственно в точках
. Силы приложены соответственно в точках 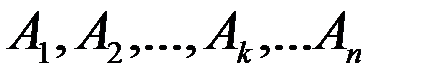 , и их линии действия пересекаются в точке О.
, и их линии действия пересекаются в точке О.
Перенося силы вдоль их линий действия в точку О, получим систему сил, приложенных в точке.
Используя правило параллелограмма, геометрически суммируем силы, приложенные в точке О. В результате получаем, что сходящуюся систему сил можно заменить одной силой, равной геометрической сумме всех сил, приложенных в точке О, – равнодействующей  :
:
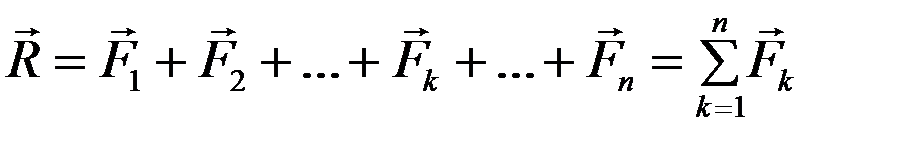 . (1.1)
. (1.1)
Правило параллелограмма для геометрического определения равнодействующей 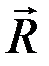 применять неудобно из-за громоздкости построений, наносимых на основной чертёж. Для этого используется правило силового многоугольника.
применять неудобно из-за громоздкости построений, наносимых на основной чертёж. Для этого используется правило силового многоугольника.
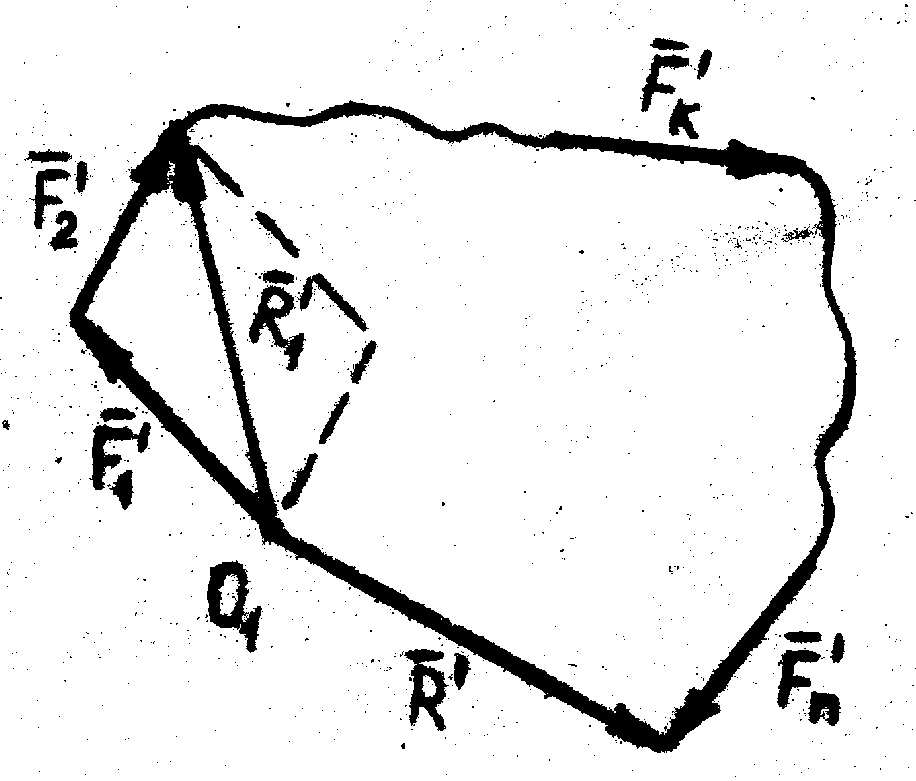
| Рис. 16 |
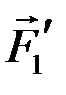 , геометрически равную силе
, геометрически равную силе 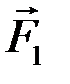
 . К концу силы
. К концу силы 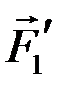 прикладываем силу
прикладываем силу 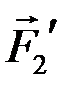
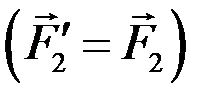 и т.д. до последней силы
и т.д. до последней силы 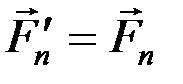 .
.
Соединяя точку О с концом силы 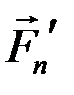 , получим силу
, получим силу 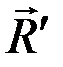 , равную геометрической сумме всех сил и называемую главным вектором данной системы сил.
, равную геометрической сумме всех сил и называемую главным вектором данной системы сил.
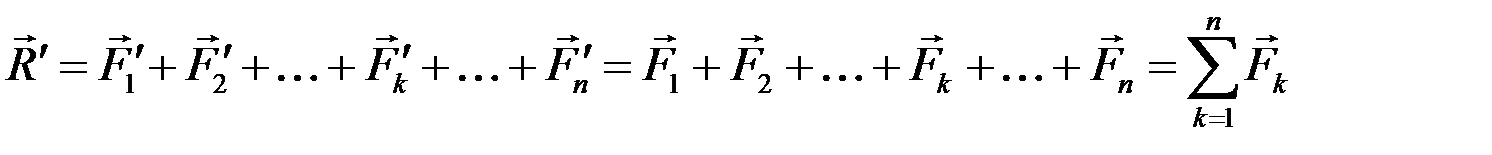 . (1.2)
. (1.2)
Перенося 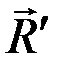 в точку О (рис. 15), получим равнодействующую
в точку О (рис. 15), получим равнодействующую 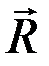 данной системы сходящихся сил.
данной системы сходящихся сил.
Правило силового многоугольника можно рассматривать как многократное применение правила параллелограмма (рис. 16).
Для равновесия сходящейся системы сил необходимо и достаточно, чтобы её равнодействующая 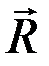 равнялась нулю:
равнялась нулю:
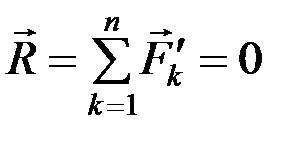 . (1.3)
. (1.3)
Геометрически условие (1.3) выражается в замкнутости силового многоугольника – конец последней силы 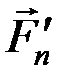 совпадает с началом первой
совпадает с началом первой 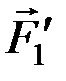 (с точкой О1 на рис. 17).
(с точкой О1 на рис. 17).
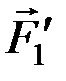
|
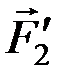
|
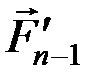
|
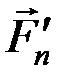
|
| О1 |
| Рис. 17 |
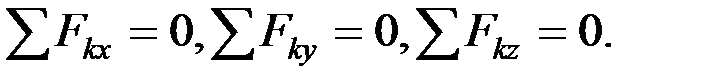 (1.4)
(1.4)
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на три координатные оси равнялись нулю.
Аналитические условия равновесия плоской системы сходящихся сил определяются двумя уравнениями:
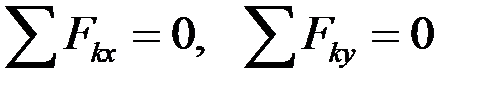 . (1.5)
. (1.5)
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы их проекций на две координатные оси равнялись нулю.
Дата добавления: 2016-01-03; просмотров: 1165;
