ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ И ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА

При изменении силы тока в проводящем контуре изменяется вели-чина магнитного потока, сцепленного с этим контуром. Следовательно в последнем, согласно закону Фарадея, будет индуцироваться электродвижущая сила (эдс). Возникновение эдс индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Эдс самоиндукции пропорциональна скорости изменения силы тока в контуре

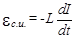. (1)

Коэффициент пропорциональности L называется индуктивностью или коэффициентом самоиндукции и измеряется в генри (Гн). Индук-тивность контура является мерой его "инертности" по отношению к изменению силы тока в нем и зависит от размеров контура, его геометрической формы, плотности намотки проводника и относительной магнитной проницаемости среды m, из которой изготовлен сердечник.

Если электрическую цепь, содержащую последовательно соединен-ные резистор с омическим или активным сопротивлением R, катушку индуктивности L и конденсатор электроемкости С, подключить к источнику переменного напряжения, то в такой цепи возникнет переменный электрический ток (рисунок 1).

Пусть напряжение источника изменяется по гармоническому закону

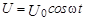, (2)

где U₀ - амплитудное значение напряжения.

Тогда ток в цепи будет равен

, (3)

где I₀ - амплитудное значение силы тока;

j - разность (сдвиг) фаз между приложенным напряжением и силой тока.

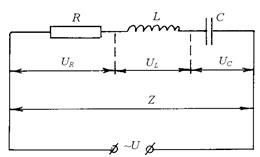Рисунок 1

Падения напряже-ния на отдельных учас-тках цепи определяются соотношениями

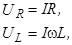(4)

,

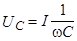где w - циклическая частота (w = 2pn);

R – активное сопро-тивление;

R_L = wL - индуктивное сопротивление;

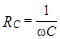- емкостное сопротивление.

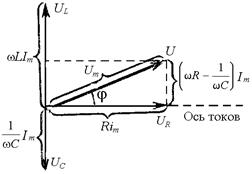Рисунок 2

В цепи переменного тока имеет место сдвиг по фазе между U_R, U_L и U_C, что можно предста-вить на векторной диа-грамме (рисунок 2). Ко-лебания напряжения на емкости отстают по фазе от колебаний силы тока на p/2, а колебания нап-ряжения на индуктив-ности опережают колебания силы тока на p/2. Напряжение на активном сопротивлении изменяется в фазе с током.

Эффективные или действующие значения силы тока I_д и напряже-ния U_д связаны с амплитудными значениями переменного тока I₀ и U₀ соотношениями

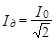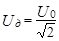, . (5)

Закон Ома для RLC – цепи (рисунок 1) имеет вид

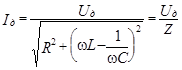, (6)

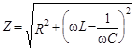где (7)

- полное электрическое сопротивление сопротивление (или импеданс);

R - активное (или омическое) сопротивление;

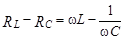(8)

- реактивное сопротивление (или реактанс).

Сдвиг по фазе между током в цепи и приложенным напряжением (рисунок 2) определяется соотношением

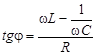. (9)

В частном случае, если цепь переменного тока содержит лишь резистор R и катушку индуктивности L, формула (6) имеет вид

,

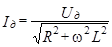где 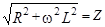, откуда

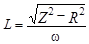. (10)

Таким образом, для определения индуктивности катушки необходимо знать ее полное сопротивление Z, активное сопротивление R и циклическую частоту w переменного тока, которая связана с обычной часто-той n соотношением w = 2pn. Для промышленного тока частота n = (50 ± 1) Гц.

4 ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1 Катушка индуктивности.

2 Ферромагнитный сердечник.

3 Конденсатор.

4 Реостат.

5 Вольтметр.

6 Амперметр.

7 Источник переменного напряжения.

8 Мост постоянного тока.

5 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1

Определение индуктивности катушки

1 Измерить с помощью моста постоянного тока активное сопротивление катушки R и определить погрешность DR.

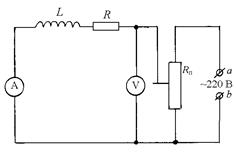Рисунок 3

2 Выбрать диапазоны и оп-ределить цену деления вольтметра и амперметра.

3 Собрать схему (рисунок 3). Здесь А и V - амперметр и вольтметр, L – исследуе-мая катушка, R_п – потен-циометр. К клеммам аb приложено переменное напряжение 220 В.

4 Замкнуть цепь и определить силу тока, идущего че-рез катушку, для трех различных напряжений U_д на ее концах.

Вычислить Z по формуле 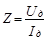и найти среднее значение <Z>.

Вычислить абсолютную погрешность DZ по формуле

,

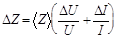где DU и DI - соответственно приборные ошибки вольтметра и ампер-метра.

Найденные значения <Z>, <R> и w подставить в формулу (10) и определить искомую индуктивность <L>.

Определить абсолютную погрешность DL по формуле

.

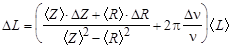5 Повторить опыт для одного значения напряжения U_д, вкладывая в катушку поочередно различные сердечники.

Найти индуктивность L катушки с сердечником и вычислить абсо-лютную погрешность измерения DL (по п. 4).

6 Полученные результаты измерений и вычислений занести в таблицу 1.

7 Результаты вычислений записать в виде:

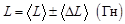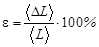; - без сердечника;

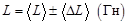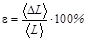; - сердечником.

Таблица 1

	U, B	DUпр B	I, мА	DIпр мА	Zi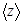, Ом	Ом	DZi, Ом	Ом	L, Гн	DL, Гн
Без сердечника
С сердеч-ником

Упражнение 2

Проверка закона Ома для цепи переменного тока

1 Выполнить п.п. 1 и 2 упражнения 1.

2 Собрать схему (рисунок 4). Здесь А и V - амперметр и вольтметр, L - катушка индуктивности, С - конденсатор, R_п - потенциометр. К клем-мам аb приложено переменное напряжение 220 В.

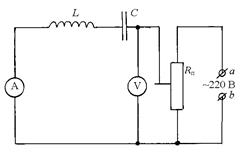Рисунок 4

3 Замкнуть цепь и определить силу тока для трех различных значений нап-ряжений U_д на ее концах.

Вычислить Z по фор-муле 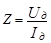и найти среднее значение <Z>.

Вычислить абсолютную погрешность DZ по формуле

,

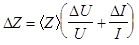где DU и DI - соответственно приборные погрешности вольтметра и амперметра.

Результаты вычислений записать в виде:

, .

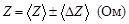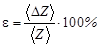4 Вычислить Z по формуле (7) и записать результат.

5 Сравнить результаты п.п. 3 и 4 и сделать вывод.