ИССЛЕДОВАНИЕ МАГНИТНЫХ СВОЙСТВ ФЕРРОМАГНЕТИКОВ
По магнитным свойствам физические тела можно разделить на три класса: диамагнетики, парамагнетики и ферромагнетики.
Диамагнетики характеризуются относительной магнитной прони-цаемостью m £ 1, т.е. эти тела, внесенные в магнитное поле, ослабляют его. К диамагнетикам относятся инертные газы, дистиллированная вода, медь, золото, серебро, цинк, висмут, т.е. тела, атомы и молекулы которых характеризуются близким к нулю магнитным моментом в отсутствии магнитного поля.
Парамагнетики характеризуются m ³1. Они несколько усиливают магнитное поле, обычно на сотые доли процента, если их внести в это поле. Атомы парамагнетиков имеют небольшой магнитный момент и в отсутствии магнитного поля. К парамагнетикам относятся щелочные металлы, алюминий, кислород, азот.
Наиболее ярко магнитные свойства проявляются у ферромагнетиков, для которых m >> 1, то есть при внесении во внешнее магнитное поле они усиливают его во много раз. К ферромагнетикам относятся железо и его сплавы, в том числе широко используемые в постоянных магнитах алюминиево-никелевые стали, никель, кобальт, полупроводниковые соединения типа MeO×Fe2O3, называемые ферритами, используемые в радиоэлектронике и элементах вычислительной техники.
Теория ферромагнетизма может быть вкратце сведена к следующим положениям: в ферромагнетиках при температурах, не превышающих критических значений, характерных для каждого типа ферромагнетика и называемых точкой Кюри (например, для железа точка Кюри равна 770 0С), существуют небольшие области с размерами 10-4...10-6 м, самопроизвольно намагниченные до насыщения, это - магнитные домены. Магнитные моменты различных доменов в отсутствии внешнего магнитного поля ориентированы хаотично, поэтому весь ферромагнетик в целом практически не обладает магнитным моментом, намагниченность его близка к нулю.
Причиной образования доменов является взаимодействие собственных (спиновых) магнитных моментов электронов в атомах ферромагнетиков, приводящее к ориентации их моментов в одном направлении. Поскольку энергия магнитного поля возрастает пропорционально квадрату магнитного момента, то энергетически невыгодно, чтобы все тело, либо его крупные части, были намагничены в одном направлении, именно поэтому происходит дробление магнетика на домены, сравнительно небольшие магнитные моменты которых компенсируют друг друга.
Совершенно отличной от других магнетиков является зависимость вектора намагниченности ферромагнетика 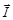 и магнитной индукции
и магнитной индукции 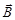 от напряженности внешнего магнитного поля
от напряженности внешнего магнитного поля 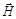
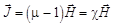 , (1)
, (1)
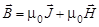 , (2)
, (2)
где c - магнитная восприимчивость ферромагнетика;
m0 = 4p×10-7 Гн/м - магнитная постоянная.
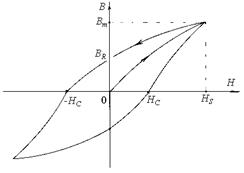 Рисунок 1
Рисунок 1
|
Эти зависимости носят нелинейный характер и образуют кривую, называемую петлей гистерезиса (от греческого - запаздывание). На ри-сунке 1 показан общий вид зависимости В = f(H).
При увеличении напряженности магнитного поля до некоторого значения HS наступает предельное значение Вm при полном, насыщаю-щем значении намагниченности тела сердечника JS. При уменьшении напряженности магнитного поля до нуля, образец сохраняет остаточную магнитную индукцию BR (остаточную намагниченность JR). Это свойство ферромагнетиков используется в элементах памяти вычислительных машин и в постоянных магнитах.
Если изменить направление магнитного поля на противоположное первоначальному, то при значении напряженности "-HC " намагничен-ность тела сердечника обращается в нуль. Такое значение напряжен-ности магнитного поля, при котором остаточная намагниченность исчезает, называется коэрцитивной силой. Магнитотвердые материалы характеризуются коэрцитивной силой HC > 400 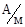 , а магнитомягкие характеризуются HC < 10
, а магнитомягкие характеризуются HC < 10 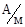 . Площадь петли гистерезиса пропорцио-нальна работе по перемагничиванию единицы объема ферромагнетика. Поэтому понятно, что магнитомягкие материалы, характеризуемые узкой петлёй гистерезиса, используются в сердечниках трансформато-ров, то есть там, где надо снижать потери энергии на перемагничивание, а магнитотвердые стали используются в постоянных магнитах.
. Площадь петли гистерезиса пропорцио-нальна работе по перемагничиванию единицы объема ферромагнетика. Поэтому понятно, что магнитомягкие материалы, характеризуемые узкой петлёй гистерезиса, используются в сердечниках трансформато-ров, то есть там, где надо снижать потери энергии на перемагничивание, а магнитотвердые стали используются в постоянных магнитах.
4 ПРИБОРЫ И ПРИНААДЛЕЖНОСТИ
1 Тороидальный трансформатор.
2 Электронный осциллограф.
3 Понижающий трансформатор 220/42.
4 Источник питания (УИП-2, или делитель напряжения).
5 ОПИСАНИЕ УСТАНОВКИ
Принципиальная схема лабораторной установки для изучения фер-ромагнетиков в переменном магнитном поле изображена на рисунке 2. В качестве исследуемого образца используется ферромагнитный сердечник тороидального трансформатора Т, первичная обмотка которого питается от потенциометра Rп , подключенного к источнику переменного напряжения U = 42 В. Возникающий при этом ток I1 создает на сопротивлении R1 падение напряжения Ux, связанное с напряженностью переменного магнитного поля H трансформатора T соотношением
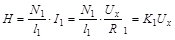 ,
, 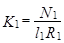 , (3)
, (3)
где l1 - длина первичной обмотки трансформатора Т (средняя длина тороидального сердечника); I1 - сила тока, намагничивающего образец; N1 - число витков первичной обмотки.
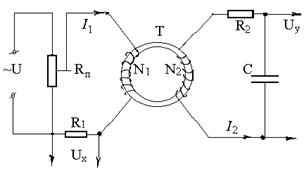 Рисунок 2
Рисунок 2
|
Таким образом, на вход X осциллографа подается напряжение Ux, пропорциональное напряженности Н магнитного поля тороидального трансформатора Т.
Для измерения магнитной индукции В в ферромагнитном сердечни-ке тороидального трансформатора Т применяется метод, основанный на законе электромагнитной индукции
e = - 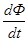 .
.
Поскольку потокосцепление
Ф = BSN2,
где S - сечение тороида;
N2 - число витков вторичной обмотки трансформатора Т, то
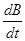 =
= 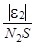 .
.
Следовательно, напряжение во вторичной обмотке пропорционально производной 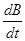 . Для того чтобы подать на вход Y осциллографа напряжение Uy, пропорциональное В, необходимо между вторичной обмоткой трансформатора Т и входом Y осциллографа включить интегрирующую цепочку R2C (рисунок 2). Действительно, преобразовав предыдущее выражение, получим
. Для того чтобы подать на вход Y осциллографа напряжение Uy, пропорциональное В, необходимо между вторичной обмоткой трансформатора Т и входом Y осциллографа включить интегрирующую цепочку R2C (рисунок 2). Действительно, преобразовав предыдущее выражение, получим
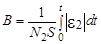 , (4)
, (4)
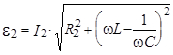 - закон Ома для переменного тока,
- закон Ома для переменного тока,
где I2 - ток во вторичной обмотке трансформатора Т;
R2 -активное сопротивление (рис. 2).
ЭДС самоиндукции вторичной обмотки считаем незначительной, т.к. число витков невелико.
R2 и C подобраны таким образом, что индуктивное и емкостное сопротивления пренебрежимо малы по сравнению с активным R2, тогда 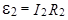 и
и
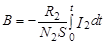 , (5)
, (5)
где 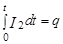 - величина заряда на обкладках конденсатора C. Следовательно,
- величина заряда на обкладках конденсатора C. Следовательно,
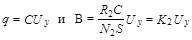 ,
, 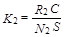 .
.
Таким образом, напряжение Uy на конденсаторе C, подаваемое на вход Y осциллографа, пропорционально индукции магнитного поля B в ферромагнитном сердечнике тороидального трансформатора Т.
При подаче напряжения Ux на горизонтально отклоняющие пластины, а Uy - на вертикально отклоняющие пластины происходит сложение двух взаимно перпендикулярных колебаний электронного луча. В результате за полный период колебаний луч воспроизводит на экране осциллографа в определенном масштабе петлю гистерезиса, которая может служить основой для изучения магнитных характеристик ферромагнетиков.
6 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
а) Подготовка установки к измерениям
1 Включить осциллограф, прогреть его 5...7 минут.
2 Установить ручки управления усилением входных сигналов осциллографа по осям "X" и "Y" в нулевое положение.
3 Электронный луч осциллографа сфокусировать в центр экрана.
4 Включить рабочую установку через понижающий трансформатор 220/42 в сеть и подключить ее к осциллографу. Напряжения установки Ux и Uy подаать соответственно к входам X и Y осциллографа (при этом клеммы “Земля” осциллографа и установки соединяются между собой).
5 Ручку потенциометра Rп установить в положение, соответствующее максимальному напряжению на первичной обмотке трнсформатора Т и получению насыщенной петли гистерезиса на экране осциллографа.
6 Ручками “Усиление" и "Синхр” добиться оптимального расположения насыщенной петли гистерезиса на экране осциллографа (при дальнейших измерениях эти ручки не трогать).
б) Проведение измерений
1 Измерить (в делениях шкалы по осям X и Y) коэрцитивную силу 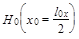 и остаточную магнитную индукцию
и остаточную магнитную индукцию 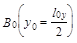 на по-лученной петле гистерезиса (l0x и l0y- длины сечения площади петли осью X и Y). Результаты измерений занести в таблицу 1.
на по-лученной петле гистерезиса (l0x и l0y- длины сечения площади петли осью X и Y). Результаты измерений занести в таблицу 1.
Таблица 1
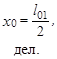
| U0x, B | H0, A/м | 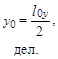
| U0y, B | B0, Тл |
2 Отключив усиление по оси Y (отсоединить установку от входа “Усиление Y” осциллографа), измерить длину отрезка lx1, соответствующего сигналу на входе X. Тоже произвести с усилением по оси X, измерив длину отрезка ly1 по оси Y. Измеренные значения x1 и y1 занести в таблицу 2 (столбец “насыщение”, 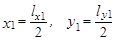 ).
).
Таблица 2
| i | Насы-щение | Д о н а с ы щ е н и я | |||||
xi= 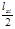 
| |||||||
| Uxi (В) | |||||||
| Hi (A/м) | |||||||
yi= 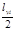
| |||||||
| Uyi (В) | |||||||
| Bi (Тл) | |||||||
| mI |
3 Уменьшая петлю гистерезиса с помощью потенциометра Rп установки, провести такие же измерения lxi и lyi для 5 различных петель. Занести значения 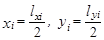 в таблицу 2.
в таблицу 2.
4 Произвести градуировку осциллографа по пункту в).
в) Градуировка экранной сетки осциллографа
1 Отключить рабочую установку от осциллографа.
Таблица 3
| i | ||||||
| Uxi (В) | ||||||
xi= 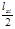 
| ||||||
| Uyi (В) | ||||||
yi= 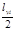
|
2 Подать на “Вход X” напряжение Uxi от источника постоянного тока (делителя) и замерить длину lxi соответствующего ему сигнала на экранной сетке осциллографа. Результаты измерений xi= 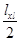 и Uxi занести в таблицу 3 и построить градуировочный график xi=f(Uxi).
и Uxi занести в таблицу 3 и построить градуировочный график xi=f(Uxi).
3 Аналогичные измерения провести по оси Y, подавая напряжения Uyi на “Вход Y” и замеряя длину lyi. Результаты y i = 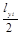 и Uyi занести в таблицу 3 и построить зависимость yi=f(Uyi).
и Uyi занести в таблицу 3 и построить зависимость yi=f(Uyi).
г) Обработка результатов измерений
1 Рассчитать напряженность Hi и магнитную индукцию Bi по формулам
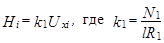
и
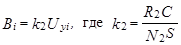
Результаты расчетов занести в таблицу 2.
H0=k1U0x, B0=k2U0y - занести в таблицу 1.
2 Построить основную кривую намагничивания Bi=f(Hi) по данным таб-ллицы 2.
3 Рассчитать относительное значение магнитной проницаемости по формуле 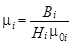 , занести эти значения в таблицу 2 и построить график зависимости mi = f(Hi).
, занести эти значения в таблицу 2 и построить график зависимости mi = f(Hi).
4 По графику mi = f(Hi) определить максимальное значение магнитноц проницаемости mmax и ее начальное значение 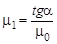 (a опредляется по наклону касательной, проведенной в начальной точке кривой Bi=f(Hi)).
(a опредляется по наклону касательной, проведенной в начальной точке кривой Bi=f(Hi)).
5 Полученные характеристики ферромагнетика занести в таблицу 4.
Таблица 4
| Данные | mmax | m1 | H0, А/м | B0, Tл |
| Лабораторные | ||||
| Справочные | ||||
| Отклонение |
| <== предыдущая лекция | | | следующая лекция ==> |
| ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ЗАРЯДА ЭЛЕКТРОНА К ЕГО МАССЕ МЕТОДОМ МАГНЕТРОНА | | | ОПРЕДЕЛЕНИЕ ИНДУКТИВНОСТИ КАТУШКИ И ПРОВЕРКА ЗАКОНА ОМА ДЛЯ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА |
Дата добавления: 2016-01-03; просмотров: 2345;
