Кинематический анализ рычажных механизмов

Кинематический анализ механизмов включает вопросы изучения звеньев с геометрической точки зрения, т.е. без учета действующих сил. Для этого используются графические, аналитические и экспериментальные методы исследования.

Одним из наглядных методов является графоаналитический, который включает:

а) построение планов положения механизма; б) определение скоростей и ускорений характерных точек или звеньев механизма.

При графических построениях на чертеже изображаются длины звеньев, скорости, ускорения и др. величины в определенном масштабе, характеризуемом масштабным коэффициентом:

m=значение параметра/длина отрезка.

Например, вектор paдлиной 10 мм изображает скорость V=20 м/с. Тогда m_v=20/10=2 м·с^-1/мм.

Построение планов положения механизма

Графическое изображение взаимного расположения звеньев механизма, соответствующее заданному моменту времени, называется планом положений или планом механизма.

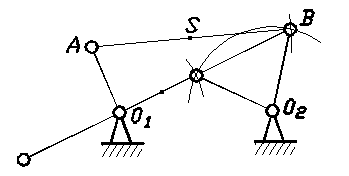
Рис. 14

Планы положения строятся в определенном масштабе методом засечек в соответствии с формулой строения механизма, При этом должны быть заданы линейные размеры всех звеньев (рис.14).

После построения нескольких совмещенных планов механизма при необходимости можно определить графически траектории характерных точек звеньев, имеющих сложное движение, например, центра тяжести S шатуна AB (рис.14).

Определение скоростей и ускорений механизма методом планов

Метод планов является одним из самых наглядных. Определению подлежат линейные скорости и ускорения отдельных точек и угловые скорости и ускорения звеньев. При этом предварительно составляются векторные уравнения для скоростей и ускорений точек звеньев, совершающих сложное движение, например:

а) звено совершает плоскопараллельное движение, состоящее из переносного, т.е. поступательного со скоростью полюса и относительного вращательного вокруг полюса (рис.15).

Принимая за полюс т. A, получим:

V_B=V_A+V_BA; где V_BA=w·l_AB;

a_B=a_A+a_BA; где a_BA=aⁿ_BA+a^t_BA при

aⁿ_BA=w²·l_AB; a^t_BA=e·l_AB.

Здесь V, a, w, e - линейные скорости и ускорения соответствующих характерных точек, а также угловые скорость и ускорение звена (индексы соответствуют характеру ускорений и обозначениям точек).

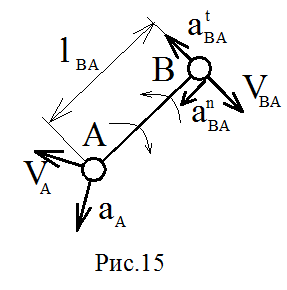
б) звено совершает сложное движение, состоящее из переносного вращательного и относительного поступательного, например, звено 1 (рис.16).

Пусть B₁ и B₂ – точки, принадлежащие звеньям 1 и 2. Тогда:

V_B1=V_B2+V_B1B2, где V_B2=w·l_AB.

a_B1=a_B2+a^t_B1B2+a^k_B1B2, где ускорение Кориолиса

a^k_B1B2=2V_B1B2·w и совпадает с направлением вектора V_B1B2, повернутого на 90^○ в сторону переносного вращения.

Решение векторных уравнений осуществляется графически путем построения так называемых планов скоростей и ускорений, на которых абсолютные скорости и ускорения откладываются от одной точки, называемой полюсом, в определенном масштабе.

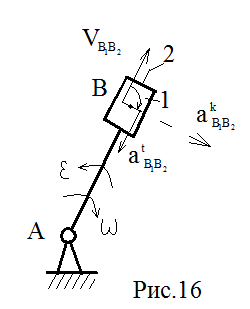
Пример расчета кривошипно-ползунного механизма рассмотрен на рис.17, где план положений (рис.17, а), план скоростей и ускорений (рис.17, б, в).

Векторные уравнения для скоростей записываются в виде:

V_B=V_A+V_BA; V_B=V_Bx+V_BBx;

где V_A=w₁·l_OA; V_Bx=0; V_BA_|_AB; V_BBx||x-x,

т.е. в выбранном масштабе μ_V: pb||x-x; ab_|_AB

V_BA= μ_V·ab; V_B= μ_V·pb и w₂= V_BA/ l_AB.

Векторные уравнения для ускорений при w₁=const записываются в виде:

a_B=a_A+a_BA; a_B=a_Bx+a^k_BBx+a^t_BBx; где a_A=aⁿ_A=w₁²·l_OA; a_BA=aⁿ_BA+a^t_BA;

здесь aⁿ_BA=w₂²·l_AB; a^t_BA=ε₂·l_AB; a_Bx=0; a^k_BBx=0; a^t_BBx||x-x.

Все ускорения представлены на рис.17 в выбранном масштабе μ_a в виде соответствующих отрезков, например, a_B=μ_a·πb и т.д.

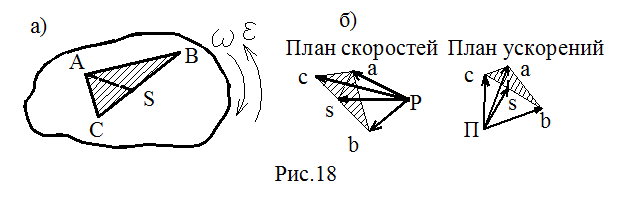При определении скоростей и ускорений промежуточных точек звеньев, например т. S, можно использовать так называемую теорему подобия, согласно которой точки на плане положений звеньев и соответственные точки на планах скоростей и ускорений образуют подобные фигуры или пропорциональные отрезки. Рассмотрим доказательство данной теоремы. На рис.18 показано звено ABC и планы скоростей и ускорений для точек этого звена:

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ca на плане скоростей соответствует V_CA_|_CA;

отрезок ab на плане скоростей соответствует V_AB_|_AB;

отрезок bc на плане скоростей соответствует V_BC_|_BC;

т.е. треугольник abc подобен треугольнику ABC.

Ускорения относительного (вращательного) движения равны:

; ; ,

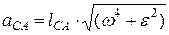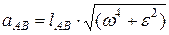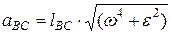т.е. a_CA/ l_CA =a_AB/ l_AB =a_BC/ l_BC или ca/CA=ab/AB=bc/BC,

Следовательно, треугольникabc подобен треугольнику ABC. Аналогичным является построение фигур для любой промежуточной точки, например т. S (рис.18, а, б).