Определение начального критического давления и расчетного сопротивления основания

Рассмотрим ленточный фундамент с глубиной заложения d на однородном основании с характеристиками γ, φ, с. Считаем, что по подошве фундамента действует давление р=F_v/A, а с боков пригрузка γd за счет веса грунта в пределах глубины заложения.

Используя формулу (3.4) и учитывая напряжения от веса грунта при ξ=1, получим следующие формулы для главных напряжений в т. М. (рис. 4.1)

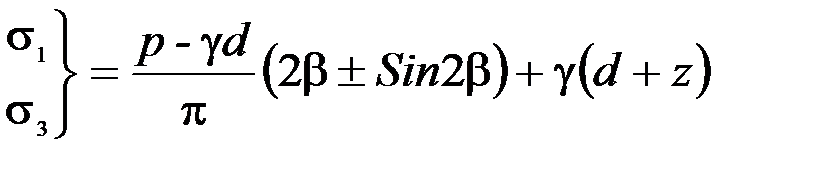(4.1)

Подставив (4.1) в УПР (2.16), получаем выражение, связывающее нагрузку р с координатами рассматриваемой т. М β, z, глубиной заложения d, характеристиками грунта γ, φ, с, т.е.

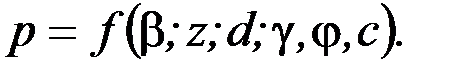(4.2)

Если в т. М выполняется УПР, то площадки сдвига совпадут с лучами из точки к краям подошвы и тогда 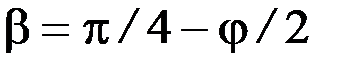, так что по (4.2) р будет зависеть только от z – максимальной глубины развития областей сдвига. Первое критическое давление получим, если примем z=0 (области сдвига полностью отсутствуют). Это решение впервые было получено профессором ПИИПСа Пузыревским Н.П. Формулу можно представить в виде:

Р_1кр =М_qγd+M_cC,

где М_q и M_c – функции угла внутреннего трения, определяемые соотношениями:

(4.4.)

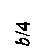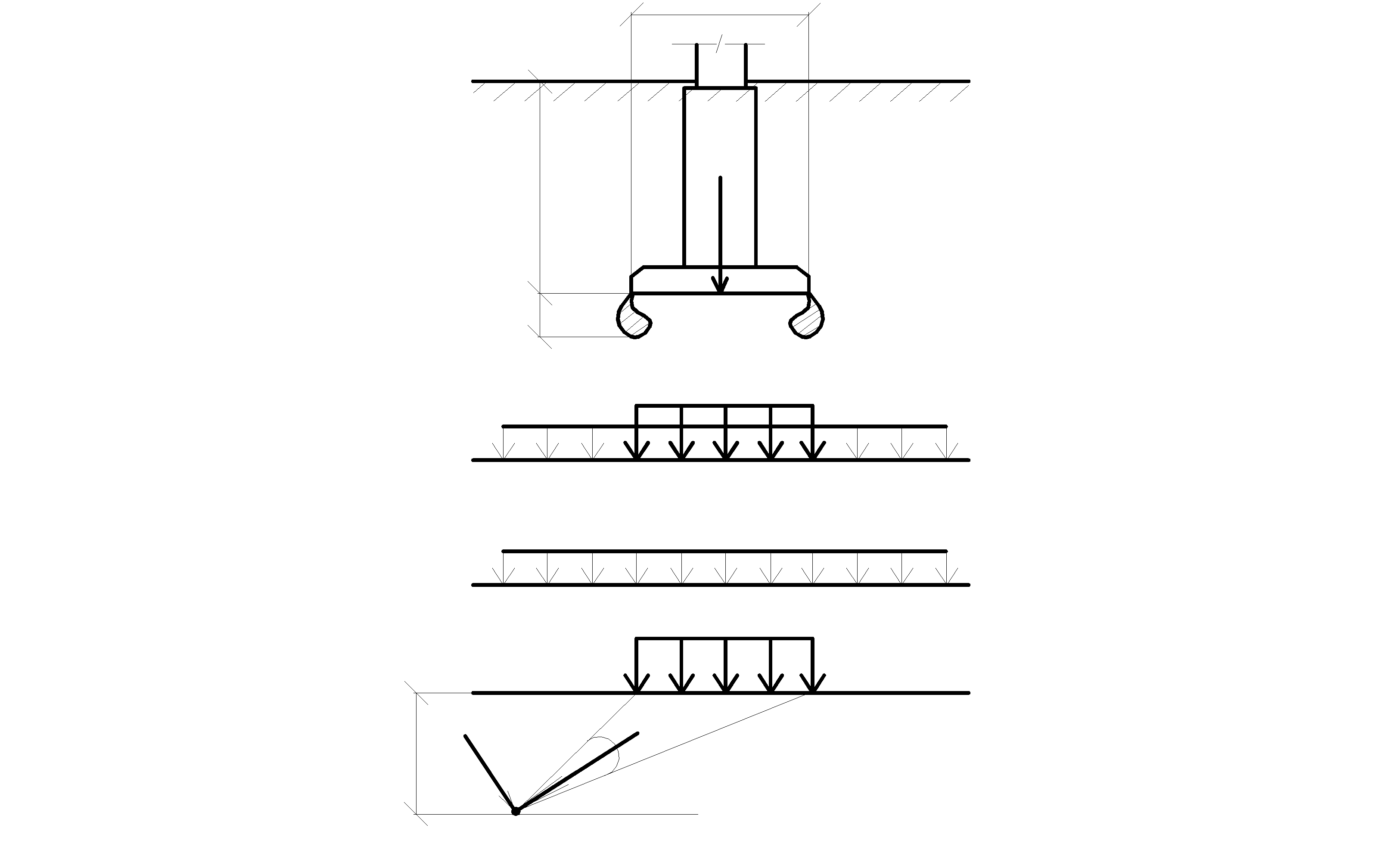
b M σ3 σ1 β β P-γd + γd γd P=FV/A FV Рис. 4.1. Расчетная схема к определению начальной критической нагрузки

Применение формулы (4.3) приводит к надежным, но не экономичным решениям; практикой доказано, что без ущерба для надежности можно допустить работу основания в начале стадии сдвигов (см. рис. 2.1), когда зависимость s = f(р) еще близка к линейной. Наибольшее применение получила формула, получаемая на основе (4.2), в которой принимается z = 0,25b. При этом (4.3) обобщается на учет ширины подошвы:

Р_нач. =М_γ γ d+M_q γd+M_c C, (4.5)

где 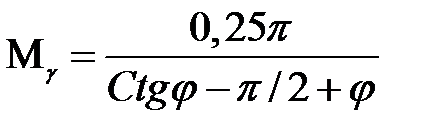, а коэффициенты M_q, M_c сохраняют указанные в (4.4) значения.

В нормах проектирования Р_нач. называется расчетным сопротивлением основания Р_нач.= R. Формула (4.5) обобщена с учетом следующих факторов:

– вид грунта и достоверность определения его характеристик;

– жесткость сооружения;

– возможность разной глубины заложения c двух сторон фундамента;

– разброс значений характеристик.