Понятие о тензоре скоростей деформации.

В теории гидродинамики показывается, что скорость 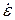деформации любого бесконечно малого отрезка, проведенного из точки А, может быть выражена (в виде линейной комбинации) через скорости линейных деформаций бесконечно малых отрезков, направленных по главным осям x, y, z и скорости изменения углов, лежащих на главных координатных плоскостях:

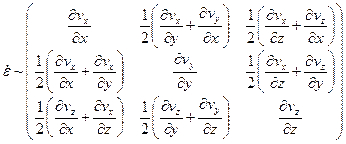
Здесь v_x, v_y, v_z – компоненты вектора скорости 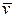в точке А.

Свойство тензора скоростей деформации.

Элементы главной диагонали тензора характеризуют скорости относительных удлинений бесконечно малых координатных отрезков 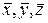. Недиагональные элементы характеризуют скорость изменения прямых углов между этими отрезками.

Скорость изменения относительного объема жидкости определяется равенством:

.

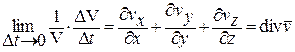Если жидкость несжимаемая, то ∆V=0.

Отсюда 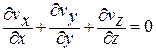или .

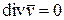Условие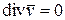

называется в гидромеханике условием несжимаемости жидкости или уравнением неразрывности потока жидкости.

Выводы: Задача расчета изменения деформированного состояния подвижной сплошной среды считается решенной, если в любой точке среды задано поле скоростей v=v(x,y,z,τ).

Соотношения Навье-Стокса (обобщенный закон И. Ньютона вязкого трения в жидкости):

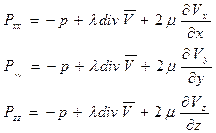(5.3)

Здесь- р – напряжение сжатия(давление) как в абс. жестком теле, остальные слагаемые –напряжения, связанные со скоростью деформации при изменении объема частицы

Запишем напряжения, связанные со скоростью деформации частиц жидкости при изменении формы частицы, т.е.– со скоростью сдвига слоев жидкости друг относительно друга.

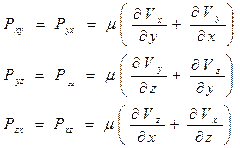
Здесь -µ - динамический коэф. вязкости.

Эти соотношения определяют модель вязкой сжимаемой жидкости (модель Навье-Стокса). Здесь [µ]=Па·с