Обработка результатов экспертизы

Методика обработки результатов экспертизы зависит от их характера и метода экспертизы [51, 52, 54]. При статистической обработке количественных данных, содержащихся в анкетах или отчетах экспертов, определяются статистические характеристики экспертных оценок, их доверительные границы, степень согласованности мнений экспертов.

Среднее значение прогнозируемой величины определяется по формуле:

где В_i– значение прогнозируемой величины, данное i‑мэкспертом; n– число экспертов в группе.

Затем определяются дисперсия прогнозируемой величины:

и приближенное значение доверительного интервала:

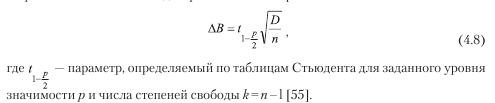
Предельные значения прогнозируемой величины определяются по формуле:

где В_в, В_н – соответственно верхняя и нижняя границы значения В.

Коэффициент вариации оценок, данных экспертами, определяется из зависимости:

где δ – среднеквадратическое отклонение значений B_i от В.

Известно, что уменьшение Vхарактеризует повышение точности прогноза.

Часто эксперт не делает численной оценки прогнозируемой величины, а лишь располагает объекты прогноза (факторы, влияющие на качество продукции или процесса, технологические методы, направления научных исследований и др.) в порядке убывания их важности или перспективности. Если имеется nобъектов оценки одного вида, то эксперт в этом случае должен установить ранг pдля каждого объекта от 1 до n. При этом высший ранг соответствует 1, низший – n. Если эксперт считает одинаково важными несколько объектов, то каждый из них получает одинаковый ранг, равный их среднеарифметическому значению.

Иногда эксперт дает две предельные оценки рассматриваемого фактора – max и min, оптимистическую и пессимистическую. Это может быть при прогнозе сроков различных событий, оценке допустимых значений каких‑то параметров продукции или процесса и т. д.

Статистическая обработка экспертных оценок в этом случае начинается с определения математического ожидания оценок i– го эксперта:

где a., b.– оптимистическая и пессимистическая оценки 1‑го эксперта. Затем определяют дисперсию этих оценок:

Математическое ожидание оценок всей группы экспертов:

где N– количество экспертов, участвовавших в опросе.

Дисперсия оценок группы экспертов:

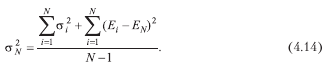
Для обработки оценок экспертов типа присоединения к одной из альтернатив строится гистограмма частот появления различных оценок. По оси абсцисс откладывают число интервалов, равное количеству рассматриваемых альтернатив, по оси ординат – количество экспертов, высказавшихся за данную альтернативу. После этого в случае рассмотрения достаточного числа (более 5) альтернатив проверяется гипотеза о нормальности распределения частот, что позволяет выбрать наиболее перспективную альтернативу, соответствующую вершине кривой распределения. Если кривую распределения построить не удается, в качестве перспективной принимается обычно альтернатива, выбранная большим числом экспертов.