ПРИНЦИПЫ ИХ КОРРЕКЦИИ
К метрологическим характеристикам СИ также относятся динамические характеристики, т.е. характеристики инерционных свойств (элементов) измерительного устройства, определяющие зависимость выходного сигнала средства измерений от меняющихся во времени величин: параметров входного сигнала, внешних влияющих величин, нагрузки. К таким характеристикам относят дифференциальное уравнение, описывающее работу средства измерений; переходную и импульсную переходную функции, амплитудные и фазовые характеристики, передаточную функцию.
Динамические свойства средства измерений определяют динамическую погрешность. Динамической погрешностью средства измерений – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.
Дифференциальное уравнение, описывающее динамический режим работы прибора прямого действия, определяется в основном дифференциальным уравнением движения подвижной части ИМ.
Для оценки динамических свойств рассматриваемых приборов используют амплитудно- и фазочастотные характеристики, так как они напрямую связаны с динамическими погрешностями приборов.
Эффективным способом улучшения динамических характеристик приборов является введение в их структуру специальных электрических схем коррекции. Коррекции подлежат элементы измерительного устройства, в которых содержатся источники динамических погрешностей.
Рассмотрим динамические характеристики магнитоэлектрического измерительного механизма, используемого в аналоговых приборах. Динамический режим этого механизма описывается уравнением:
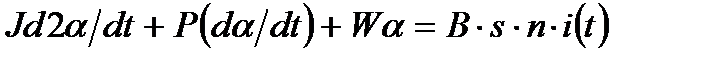 , (3.7)
, (3.7)
где J – момент инерции подвижной части измерительного механизма;
a – угол ее отклонения;
Р – коэффициент успокоения;
W – удельный противодействующий момент;
В – индукция в воздушном зазоре;
s, n – площадь и число витков рамки;
i(t) – мгновенное значение тока в рамке.
Используя принятые обозначения ( 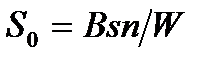 – чувствительность к постоянному току;
– чувствительность к постоянному току; 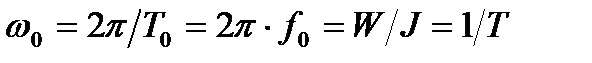 – круговая частота собственных колебаний;
– круговая частота собственных колебаний; 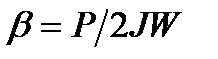 – степень успокоения) получим выражения для передаточной функции и комплексной чувствительности магнитоэлектрического прибора:
– степень успокоения) получим выражения для передаточной функции и комплексной чувствительности магнитоэлектрического прибора:
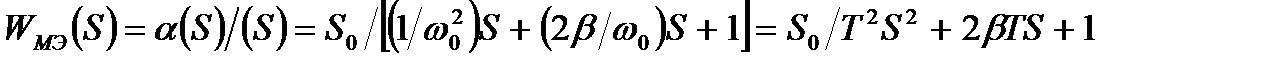 , (3.8)
, (3.8)
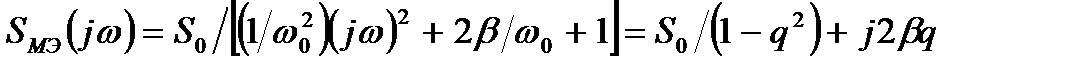 , (3.9)
, (3.9)
где 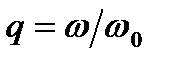 .
.
Выражение для АЧХ и ФЧХ имеют вид:
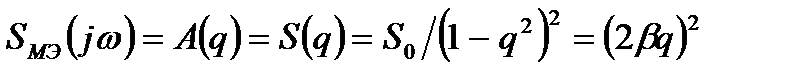 , (3.10)
, (3.10)
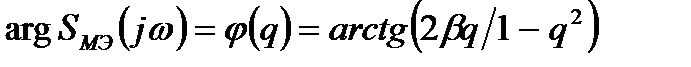 , (3.11)
, (3.11)
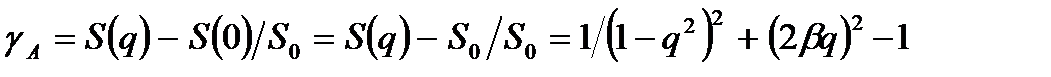 , (3.12)
, (3.12)
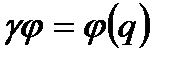 . (3.13)
. (3.13)
Из выражений для АЧХ и ФЧХ следует, что они критичны к значению степени успокоения b. Оптимальное значение b можно получить из условия минимальности погрешностей gA и gj. Погрешность gA®0 при q®0 и отсутствует при выполнении равенства:
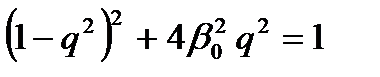 , (3.14)
, (3.14)
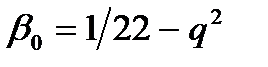 . (3.15)
. (3.15)
Условие (3.15) показывает, что оно близко к выполнению в относительно широком диапазоне частот (q = 0–0,5) при b = 0,65–0,7, т. е. этот режим обеспечивает минимальные значения погрешностей gA и gj в диапазоне частот w = (0 – 0,5)w0. .
При разработке самопишущих приборов повышенного быстродействия ставится задача получения АЧХ и ФЧХ, обеспечивающих минимальные погрешности измерения в наиболее широком диапазоне частот, то есть стремятся создать условия для оптимального режима успокоения и по возможности увеличить частоту собственных колебаний (f0) подвижной части ИМ, так как ее значение определяется частотный диапазон прибора.
Оптимальное успокоение (b0 = 0,65 – 0,7) обеспечивается обмоточным и жидким успокоением.
При использовании обмоточного успокоения внешнее сопротивление, подключаемое к рамке ИМ, нормируется и определяется выражением:
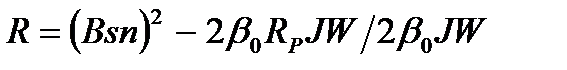 , (3.16)
, (3.16)
где RP – сопротивление рамки.
Быстродействие прибора повышают, уменьшая ширину поля записи, что приводит к росту погрешности при расшифровке графика.
В самопишущих приборах перечисленные конструктивные меры позволяют получить значения f0 в пределах 50 – 70 Гц (потребляемая прибором мощность достигает при этом предельно допустимого значения). Дальнейшее расширение частотного диапазона требует использования схемных методов (усиление исследуемого сигнала, коррекция частотной погрешности).
Усиление по мощности входного сигнала позволяет увеличить потребляемую ИМ мощность, то есть повысить f0. Применение корректирующих цепей повышает быстродействие прибора путем выравнивания АЧХ и ФЧХ в расширенном диапазоне частот.
Динамические погрешности регистрирующих средств измерений ограничиваются путем нормирования следующих величин: времени успокоения tу и допускаемого значения отношения первого отброса пишущего устройства a1m к установившемуся отклонению aуст, которое не должно превышать для самопишущих приборов допускаемой ширины пропускания частот (wH – wB), т.е. того диапазона, в котором отклонение амплитудно-частотной характеристикиA(w)от некоторого номинального значения A0, а также фазовые сдвиги j(w)не превышают заданных значений DA и Dj.
| А(W) |
| А0 |
| О(WН) |
| WВ |
| W(2пf) |
| А |
| U(W) |
| WН) |
| WВ |
| W(2пf) |
| U |
| -п/2 |
| -п |
| б) |
| а) |
| Рис. 3.1. Типовые частотные характеристики измерительного прибора: а) амплитудная; б) фазовая. |
Использование для оценки динамических свойств регистрирующих приборов их характеристик обусловлено прямой связью этих характеристик с динамическими погрешностями приборов.
Если входной сигнал x(t) = xmsinw t, а выходной y(t) = ymsin(w t + j), частотную передаточную функцию прибора («комплексную чувствительность») запишем в таком виде: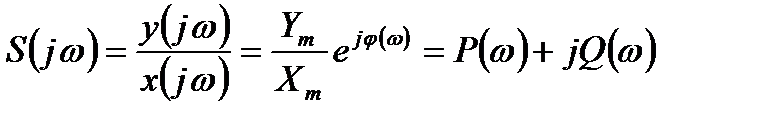 ,
,
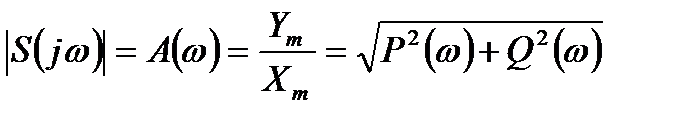 , (3.17)
, (3.17)
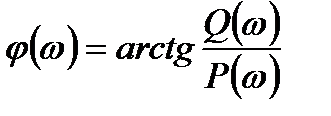 , (3.18)
, (3.18)
гдеA(w)– амплитудно-частотная характеристика (АЧХ); j(w)–фазочастотная характеристика (ФЧХ).
Относительная погрешность воспроизведения синусоидального сигнала:
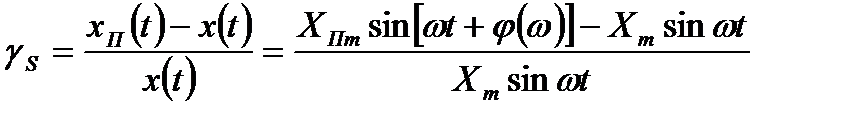 (3.19)
(3.19)
изменяется во времени и определяется амплитудными и фазовыми искажениями. Обычно рассматриваются погрешности воспроизведения амплитуды gA и фазы gj, используя их для оценок АЧХ и ФЧХ прибора:
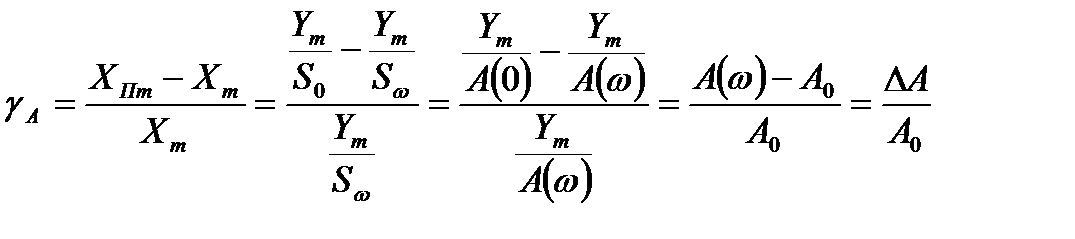 , (3.20)
, (3.20)
где S0и Sw – чувствительность прибора к сигналу, постоянному во времени, и синусоидальному сигналу частоты w.
Погрешность воспроизведения фазы:
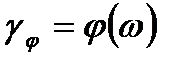 (3.21)
(3.21)
В общем случае входной сигнал x(t) можно представить спектром синусоидальных сигналов определенной частоты и амплитуды. Для неискаженного воспроизведения измеряемой величины необходимо, чтобы прибор воспроизводил все составляющие спектра сигнала с постоянной чувствительностью S0(A0), не создавая при этом фазовых сдвигов.
Достоверность воспроизведения сигнала сложной формы обеспечивается также при наличии линейной зависимости фазового сдвига от частоты:
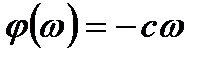 (3.22)
(3.22)
| Wn(P) |
| W1(P) |
| W1(P) |
| Wос(P) |
| Wпосл(P) |
| W1(P) |
| а) |
| б) |
| в) |
| х |
| х |
| х |
Рис. 3.2. Схема включения корректирующих звеньев:
а) последовательная; б) параллельная;
В этом случае записанная кривая xn(t) смещается по оси времени по отношению к входному сигналу x(t). Определим время смещения (запаздывания) tC. Пусть x(t) = xm sin w t, тогда получим
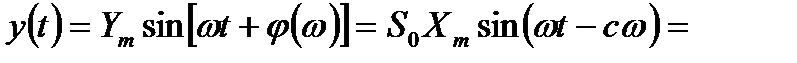
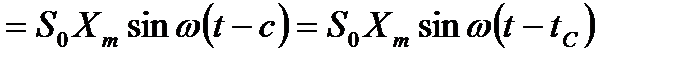 (3.23)
(3.23)
т.е. время смещения для всех гармоник одинаковое (tC=c). Поскольку временная зависимость между основной частотой и гармониками не нарушается, сигнал сложной формы воспроизводится прибором без искажений.
На рис.3.1 представлены АЧХ и ФЧХ идеального измерительного устройства, воспроизводящего входной сигнал с временным сдвигом tC.
Установлено, что для многих измерительных устройств постоянство АЧХ в некотором диапазоне частот обеспечивает в этом диапазоне отсутствие фазовых искажений. При разработке приборов стремятся по возможности получить постоянную АЧХ в широком диапазоне частот. Расширения рабочей полосы частот (увеличения wb) можно достигнуть, используя включение корректирующих звеньев со специально подобранной характеристикой, рис.3.2. Корректирующие звенья вводят в схему прибора последовательным а) и параллельным б) включением, а также выполняют в виде местной обратной связи в).
Результирующие передаточные функции при включении звеньев коррекции согласно рис.3.2 определяются выражением:
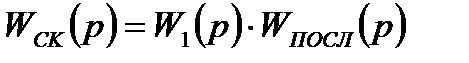 , (3.24)
, (3.24)
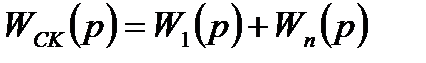 , (3.25)
, (3.25)
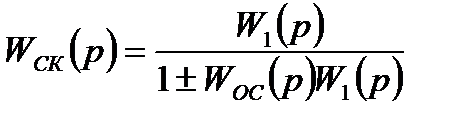 , (3.26)
, (3.26)
где W1(p); WПОСЛ(p); Wn(p); WОС(p) – передаточные функции схемы прибора (или части ее), последовательного и параллельного корректирующего звена и звена обратной связи.
На практике проектирования схем измерительных приборов Применяются обратные связи в качестве корректирующих устройств. используются дифференцирующие и интегрирующие RC – цепи, дифференцирующие трансформаторы и др. В последнее время широко применяются также корректирующие измерительные усилители – безинерционные усилители с большим коэффициентом усиления Kус, охваченные частотозависимой обратной связью, рис.3.3. Передаточная функция корректирующего измерительного усилителя имеет вид:
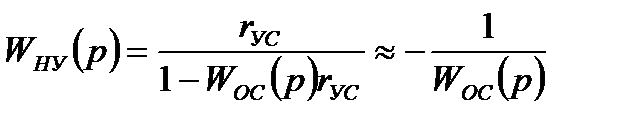 , ( WОС(p)rУС >> 1). (3.27)
, ( WОС(p)rУС >> 1). (3.27)
Функция преобразования (статическая характеристика преобразования) F(X) ─ функциональная зависимость между информативными параметрами выходного Y и входного X сигналов средства измерений Y = f (X). Функцию преобразования, принимаемую для средства измерения и устанавливаемую в научно-технической документации на данное средство, называют номинальной функцией преобразования средства. Номинальная статическая характеристика
преобразования позволяет рассчитать значение входной величины по значению
КУС
WОС(Р)
Рис.3.3. Структурная схема корректирующего измерительного усилителя.
выходной. Она может задаваться аналитически, таблично или графически. Функция преобразования может быть линейной или нелинейной и связывает входную и выходную величины с параметрами устройства измерения..
Дата добавления: 2015-12-29; просмотров: 1042;
