Пара сил и её свойства

Пусть имеются равные антипараллельные силы 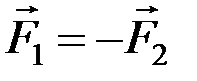, тогда 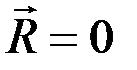; АС = ∞; ВС = ∞. Следовательно, точка С находится в бесконечности.

Система двух равных по величине параллельных и направленных в разные стороны сил называется парой сил (понятие ввел Франсуа Пуансо (1777 – 1859)).

Очевидно, что пара сил не имеет равнодействующей, следовательно, она не ведет к поступательному движению тела, а приводит тело во вращательное движение. Плоскость, в которой действует пара, называется плоскостью пары, расстояние между силами – плечом пары. Действие пары на тело зависит от величины сил, плеча и направления сил. Эта зависимость выражается в понятии момента.

Моментом пары называется вектор, величина которого равна взятому со знаком плюс или минус произведению одной из сил пары на плечо пары.

Будем считать: при знаке «+» момент направлен против часовой стрелки; при знаке «–» – по часовой стрелке. Размерность момента – Н·м.

Теорема.Не нарушая кинематического состояния тела, можно переносить пару в любое положение в плоскости её действия.

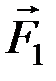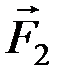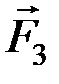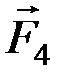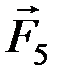Доказательство. Пусть на тело действует пара ( , ). Произвольно на таком же плече А₁В₁ возьмём две уравновешенные пары ( , ) и ( , ), эквивалентные нулю. Продлим их линии действия и сложим силы , , , .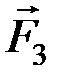

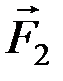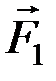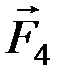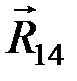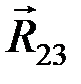Равнодействующие силы и равны по величине, направлены по одной линии (диагональ ромба) и противоположны. Остается система сил ( 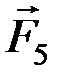, 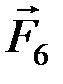), эквивалентная ( 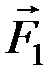, 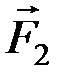). Т.к. точки A₁B₁ выбирались произвольно, теорема доказана.

Теорема.Не изменяя действия данной пары на тело, можно силу и плечо пары изменять любым способом, но так, чтобы момент пары остался неизменным.

Доказательство.

Пусть дана пара сил ( 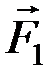, 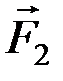) с плечом АВ. Разложим силу на составляющие 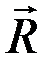и , тогда 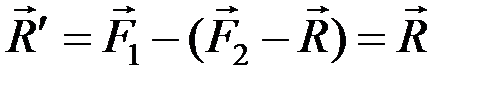, следовательно, имеем новую пару ( ).

На плече AC пара ( 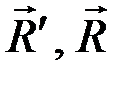) эквивалентна паре ( , 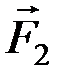), причем для любой пары плечо AC удовлетворяет условию 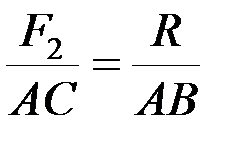или . Теорема доказана.

Таким образом, задаваясь плечом, можно определить 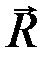, и наоборот.

Теорема.Две пары, лежащие в одной плоскости и имеющие равные моменты, статически эквивалентны.

Эту теорему доказывать не будем, т.к. она является следствием двух предыдущих теорем.

Совокупность пар называется системой пар.

Теорема.Система пар, расположенных в одной плоскости, эквивалентна одной паре с моментом, равным алгебраической сумме моментов слагаемых пар.

Доказательство. Возьмем две пары ( 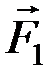, ) и ( 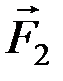, ), произвольно расположенные на плоскости. Приведем их к одинаковому плечу d. Согласно аксиоме А 3, силы 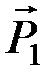, и 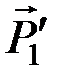, 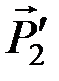можно алгебраически сложить: 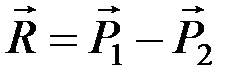; . Силы и 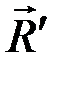равны по величине и противоположны по направлению, следовательно, это новая пара с моментом 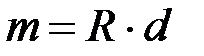, эквивалентным двум данным парам.

Нетрудно заметить, что 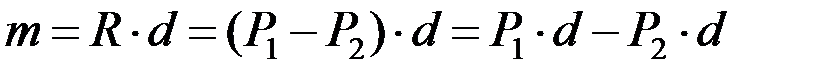. Это значит, что или 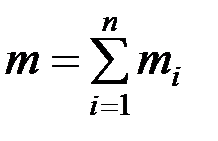(момент каждой пары должен быть взят со своим знаком).