Условия равновесия плоской системы сил

Теорема. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы были равны нулю:

,

.

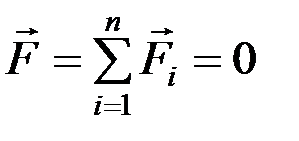Данная теорема имеет три формы.

Первая форма уравнений равновесия.

Теорема.Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух выбранных координатных осей равнялась нулю и чтобы сумма моментов всех сил системы относительно любой точки плоскости также равнялась нулю.

Т.к. , а , ,

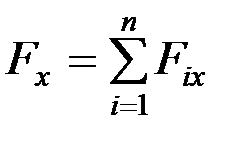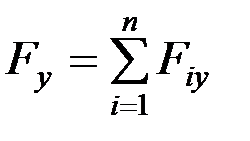то уравнения равновесия будут иметь вид:

.

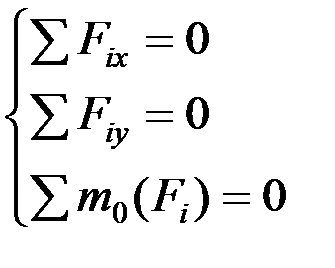Вторая форма уравнений равновесия.

Теорема.Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма моментов всех сил относительно двух произвольных точек равнялась нулю и чтобы сумма проекций всех сил на произвольную ось, не перпендикулярную прямой, соединяющей эти точки, равнялась нулю:

.

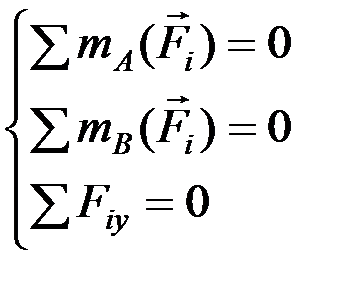Третья форма уравнений равновесия.

Теорема. Для равновесия произвольной плоскости системы сил необходимо и достаточно, чтобы суммы моментов всех сил системы относительно каждого из трёх произвольных, но не лежащих на одной прямой центров равнялись нулю.

Доказательство:

а) необходимость: это условие очевидно, т. к. если есть равновесие, то сумма моментов всех сил относительно всякого центра равна нулю;

б) достаточность: возьмём три точки A, B, C, не лежащие на одной прямой. Пусть относительно них выполняются равенства:

.

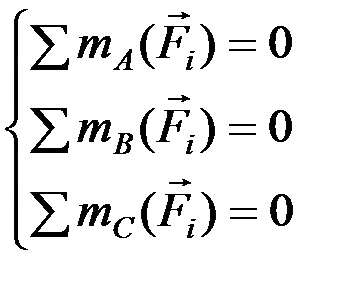Докажем, что система сил находится в равновесии.

Докажем обратное, что условия выполнены, а система сил не находится в равновесии.

Выберем точку A за центр приведения и приведем все силы к центру: получим равнодействующую 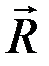, приложенную к точке A. Т.к. главный момент 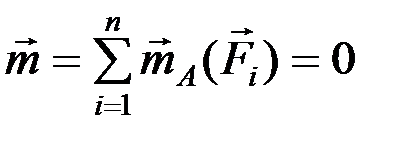, то пары не будет.

Если окажется, что R = 0, то теорема доказана ( ).

Пусть 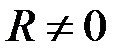, тогда линия действия 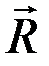должна пройти через точку B, чтобы выполнялось условие , а по теореме Вариньона, 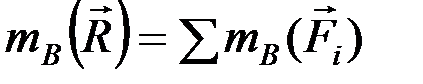. Следовательно, 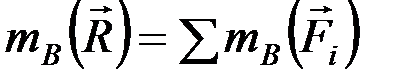, что может быть при 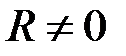только в случае, если 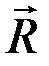проходит через точку B. Таким образом, проходит через точку A и точку B. По условию, 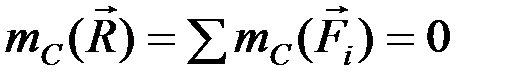. Т.к. 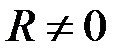, линия действия 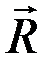должна пройти через точку C, что невозможно, следовательно, R = 0.