Приведение произвольной плоской системы сил к данному центру
Выберем точку O и назовем её центром. Пользуясь предыдущей теоремой, перенесём все силы, действующие на тело в точку O. Получим систему сходящихся сил и некоторое количество пар. Сложив полученную систему сил по известному правилу силового многоугольника, получим одну силу  , называемую главным вектором системы:
, называемую главным вектором системы:
 .
.
Складывая пары, получим результирующую пару с моментом, равным алгебраической сумме моментов слагаемых пар. Обозначив момент результирующей пары m, а моменты слагаемых пар  , получим:
, получим: 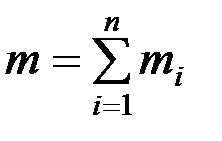 .
.
Однако ранее доказано, что
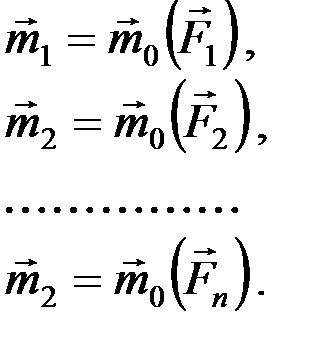
Следовательно, 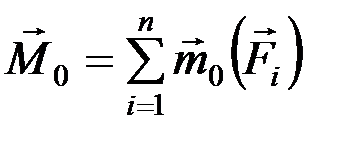 .
.
Эта сумма моментов всех сил относительно какого-либо центра приведения называется главным моментом системы.
 Всякую плоскую систему сил всегда можно заменить одной силой, равной главному вектору системы и приложенной в произвольно выбранном центре приведения, и парой с моментом, равным главному моменту системы относительно выбранного центра приведения.
Всякую плоскую систему сил всегда можно заменить одной силой, равной главному вектору системы и приложенной в произвольно выбранном центре приведения, и парой с моментом, равным главному моменту системы относительно выбранного центра приведения.
Важно отметить, чтосила 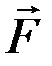 не является равнодействующей системы, т.к. она замещает систему только в совокупности с главным моментом.
не является равнодействующей системы, т.к. она замещает систему только в совокупности с главным моментом.
Для аналитического определения главного вектора проведем оси координат и спроецируем уравнение 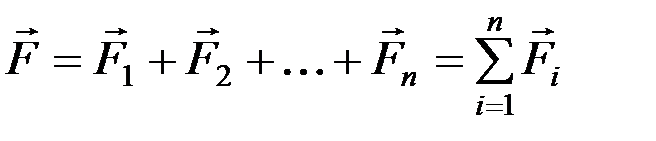 на эти оси:
на эти оси:
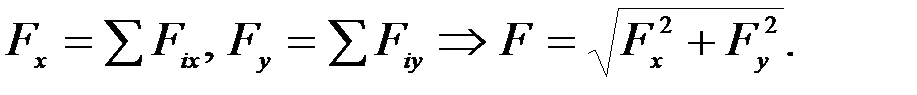
Направление главного вектора определяют направляющие косинусы:
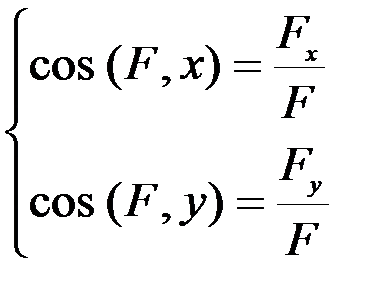 .
.
Теорема Вариньона
Момент равнодействующих сил, расположенных в одной плоскости, относительно некоторой точки равен алгебраической сумме моментов составляющих сил относительно той же точки.
Доказательство.
 Проанализируем характер распределения площадей:
Проанализируем характер распределения площадей:
 2 площади
2 площади  ;
;
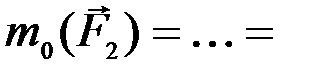 2 площади
2 площади 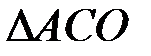 ;
;
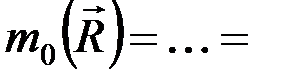 2 площади
2 площади  .
.
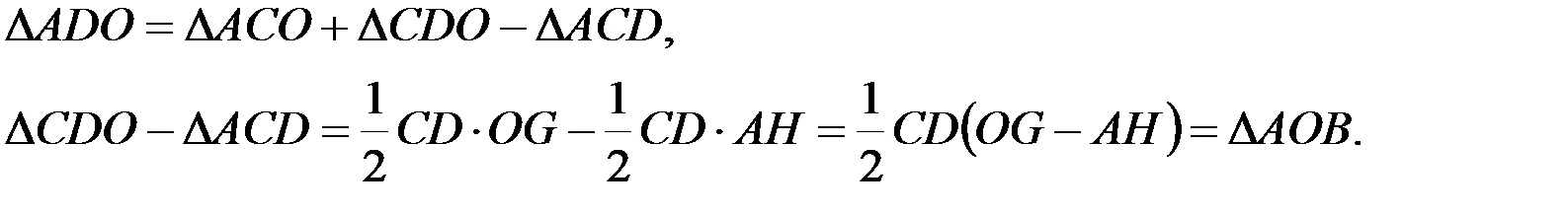
Следовательно, 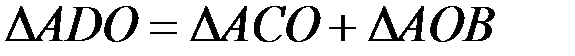 .
.
Умножив уравнение на два, получим:  .
.
Это равенство справедливо также и в векторной форме:
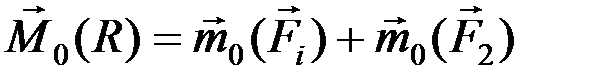 ,
,
где знак «+» следует понимать в алгебраическом смысле.
Дата добавления: 2015-12-26; просмотров: 935;
