Особые случаи симплексного метода
Не единственность оптимального решения (альтернативный оптимум)
Рассмотрим задачу:
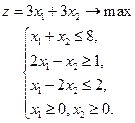
При решении задачи геометрически, мы убедились, что оптимум достигается на отрезке, принадлежащем прямой 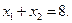 Рассмотрим этот вариант при симплекс-методе. На очередном шаге получим:
Рассмотрим этот вариант при симплекс-методе. На очередном шаге получим:
| Базис | Свободный | Переменные | Оценочные | ||||
| член | отношения | ||||||
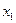
| 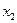
| 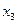
| 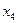
| 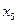
| |||
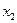
| 2/3 | 1/3 | |||||
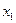
| 1/3 | -1/3 | 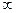
| ||||
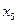
| |||||||
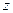
|
Здесь 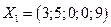 - допустимое решение и соответствует точке (3; 5) на графике. Критерий оптимальности выполнен, следовательно
- допустимое решение и соответствует точке (3; 5) на графике. Критерий оптимальности выполнен, следовательно 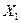 -оптимальное решение и максимальное значение функции
-оптимальное решение и максимальное значение функции 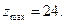 Однако в оценочной строке коэффициент перед небазисной переменной
Однако в оценочной строке коэффициент перед небазисной переменной 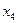 равен нулю, поэтому изменение этой переменной не повлечет изменение целевой функции, следовательно, ее можно внести в основные переменные.
равен нулю, поэтому изменение этой переменной не повлечет изменение целевой функции, следовательно, ее можно внести в основные переменные.
| Базис | Свободный | Переменные | ||||
| член | ||||||
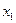
| 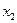
| 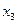
| 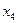
| 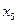
| ||
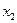
| 1/3 | -1/3 | ||||
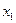
| 2/3 | 1/3 | ||||
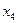
| ||||||
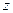
|
Получим 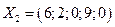 - оптимальное решение и
- оптимальное решение и 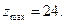 Данному решению соответствует точка (6; 2) на графике.
Данному решению соответствует точка (6; 2) на графике.
Учитывая, что переменная 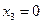 в базисном решении
в базисном решении 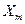 стается не основной, а удовлетворяет неравенству
стается не основной, а удовлетворяет неравенству 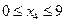 , можно получить все множество оптимальных решений.
, можно получить все множество оптимальных решений.
Пусть 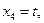
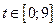 . Имеем
. Имеем
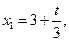
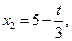
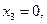
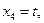
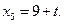
Замечании.Множество решений можно представить как выпуклую линейную комбинацию базисных решений
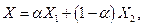
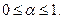
Дата добавления: 2015-11-28; просмотров: 1084;
