Анализ влияния дохода и цен на спрос
Как было показано в предыдущих параграфах, для оценки различных ситуаций в сфере потребления применяются предельный спрос и предельная полезность денег по ценам 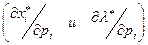 и доходу
и доходу 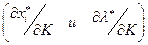 . Выведем формулы для их вычисления. Если общее решение задачи (2.4.1) - (2.4.2) для конкретной функции полезности
. Выведем формулы для их вычисления. Если общее решение задачи (2.4.1) - (2.4.2) для конкретной функции полезности  найдено в виде функций
найдено в виде функций
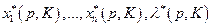 (2.6.1)
(2.6.1)
от 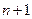 параметра
параметра 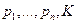 , то требуемые предельные величины можно найти, вычисляя частные производные функций (2.6.1) по
, то требуемые предельные величины можно найти, вычисляя частные производные функций (2.6.1) по 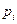 и
и 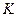 . Но эти же предельные величины можно найти, не решая задачу (2.4.1) - (2.4.2), а сразу из системы необходимых и достаточных условий оптимальности (2.4.5) - (2.4.8).
. Но эти же предельные величины можно найти, не решая задачу (2.4.1) - (2.4.2), а сразу из системы необходимых и достаточных условий оптимальности (2.4.5) - (2.4.8).
Зная, что оптимальное решение 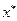 задачи (2.4.1) - (2.4.2) лежит на бюджетной линии (см. Рис. 2.7), можно априори считать, что доход
задачи (2.4.1) - (2.4.2) лежит на бюджетной линии (см. Рис. 2.7), можно априори считать, что доход 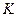 будет использован полностью. Тогда в (2.4.2) будет строгое равенство, и система (2.4.5) - (2.4.8) примет вид:
будет использован полностью. Тогда в (2.4.2) будет строгое равенство, и система (2.4.5) - (2.4.8) примет вид:
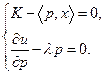 (2.6.2)
(2.6.2)
Так как эта система зависит от параметров 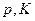 и содержит неизвестные
и содержит неизвестные 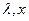 , то введём обозначения:
, то введём обозначения:
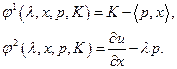 (2.6.3)
(2.6.3)
Будем предполагать, что функция 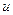 дважды непрерывно дифференцируема и удовлетворяет условиям (2.2.1) - (2.2.2).
дважды непрерывно дифференцируема и удовлетворяет условиям (2.2.1) - (2.2.2).
Система (2.6.2) будет разрешимой относительно 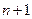 переменных
переменных 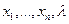 , если определитель матрицы Якоби (матрица первых производных системы (2.6.2))
, если определитель матрицы Якоби (матрица первых производных системы (2.6.2))
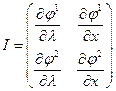
отличен от нуля. Покажем это. С учетом обозначений (2.6.3) получаем:
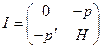
где 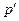 - транспонированный вектор
- транспонированный вектор 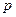 , H - матрица Гессе (матрица вторых производных системы (2.6.2)). В координатной форме матрица
, H - матрица Гессе (матрица вторых производных системы (2.6.2)). В координатной форме матрица
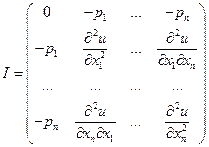
- есть «окаймляющая» ценами товаров матрица Гессе. По условию (2.2.2) матрица Гессе отрицательно определена и поэтому невырождена. Следовательно, определитель матрицы Якоби не равен нулю, и система (2.6.2) имеет решение (по 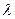 и
и 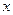 ). Вычислим требуемые предельные величины.
). Вычислим требуемые предельные величины.
1. Вычисление предельных величин 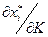 и
и 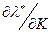 (влияние дохода на
(влияние дохода на 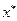 и
и 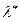 ).
).
Подставим (2.6.1) в систему (2.6.2):
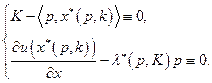 (2.6.4)
(2.6.4)
и продифференцируем её по 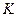 :
:
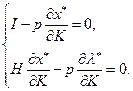
Перепишем эту систему в форме, удобной для перехода к матричной записи:
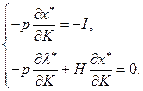
В матричной форме эта система имеет вид:
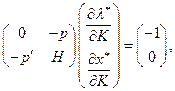 (2.6.5)
(2.6.5)
где
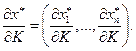
Решая систему (2.6.5), находим искомые предельные величины по доходу.
2. Вычисление предельных величин 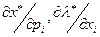 (влияние цены
(влияние цены 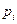 на
на 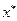 и
и 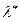 при условии постоянства остальных цен
при условии постоянства остальных цен 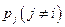 и дохода
и дохода 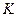 ).
).
Дифференцируя систему (2.6.4) по 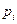 , получаем (в координатной форме):
, получаем (в координатной форме):
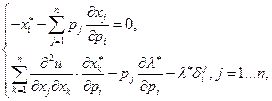 (2.6.6)
(2.6.6)
где
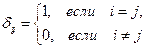
- символ Кронекера. Запишем систему (2.6.6) сначала в векторной, затем в матричной форме:
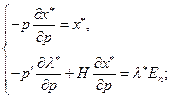
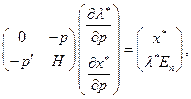 (2.6.7)
(2.6.7)
где
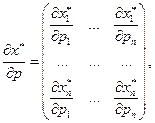
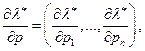
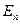 - единичная
- единичная 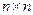 -матрица
-матрица 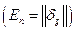 - матрица с нулевыми элементами за исключением диагональных, равных 1). Решая систему (2.6.7) , находим искомые предельные величины по цене i-го товара.
- матрица с нулевыми элементами за исключением диагональных, равных 1). Решая систему (2.6.7) , находим искомые предельные величины по цене i-го товара.
3. Вычисление предельных величин 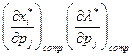 (влияние цен
(влияние цен 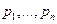 на
на 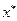 и
и 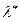 при условии компенсации дохода так, чтобы полезность была неизменной).
при условии компенсации дохода так, чтобы полезность была неизменной).
Используя систему (2.6.2), найдем полные дифференциалы функций 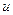 и
и 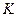 :
:
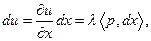
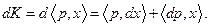
Для того чтобы полезность оставалась неизменной, т.е. чтобы 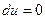 , необходимо, чтобы
, необходимо, чтобы 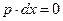 (так как
(так как 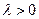 ), а это справедливо, если
), а это справедливо, если
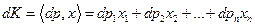 .
.
Содержательно это означает, что при возрастании, например, цены 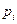 до
до 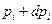 , приращение дохода, обеспечивающее неизменность полезности, равно
, приращение дохода, обеспечивающее неизменность полезности, равно 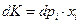 .
.
Дифференцируя (2.6.4) по 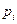 и учитывая, что
и учитывая, что 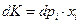 , получаем:
, получаем:
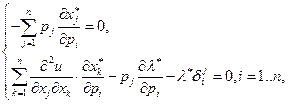
где первое уравнение этой системы получается из (2.6.6) при условии
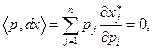
так как в этом случае из (2.6.6) следует 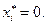 В векторной форме эта система имеет вид:
В векторной форме эта система имеет вид:
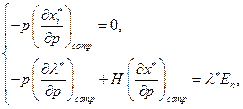
где  - означает компенсированное изменение цен. Запишем матричную форму:
- означает компенсированное изменение цен. Запишем матричную форму:
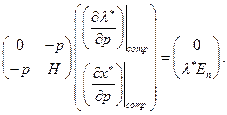 (2.6.8)
(2.6.8)
Решая систему (2.6.8), находим искомые предельные величины при компенсированном изменении цен.
Все три матричных (2.6.5) , (2.6.7) и (2.6.8) можно объединить в одно матричное уравнение:
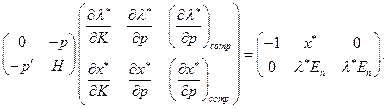 (2.6.9)
(2.6.9)
Это уравнение называется основным матричным уравнением теории потребления. Матрица
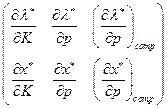
называется матрицей сравнительной статики, а ее элементы - показателями сравнительной статики. Такое название объясняется тем, что эти показатели характеризуют чувствительность 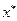 и
и 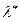 к изменениям параметров
к изменениям параметров 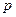 и
и 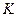 путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.
путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.
Так как левая часть уравнения (2.6.9) есть невырожденная матрица (в силу невырожденности Якобиана), то оно может быть разрешено относительно показателей сравнительной статики. Решение уравнения (2.6.9) связано с понятием уравнения Слуцкого.
Уравнение Слуцкого
Запишем основное матричное уравнение (2.6.9) в виде:
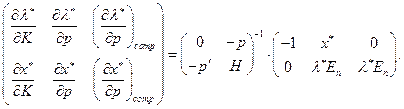 (2.7.1)
(2.7.1)
Решение этой системы относительно показателей сравнительной статики по спросу имеет вид:
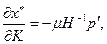 (2.7.2)
(2.7.2)
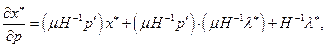 (2.7.3)
(2.7.3)
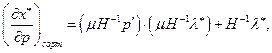 (2.7.4)
(2.7.4)
где 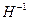 - обратная матрица Гессе, а
- обратная матрица Гессе, а
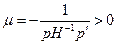
- скалярная величина. Можно показать, что
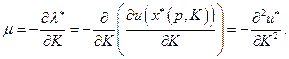
Поэтому скаляр 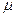 можно интерпретировать как коэффициент убывания предельной полезности денег. Сравнивая (2.7.3) и (2.7.4) замечаем, что
можно интерпретировать как коэффициент убывания предельной полезности денег. Сравнивая (2.7.3) и (2.7.4) замечаем, что
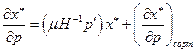
Сопоставляя это уравнение с (2.7.2) , получаем,
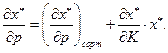 (2.7.5)
(2.7.5)
Равенство (2.7.5) называется уравнением Слуцкого. Это же уравнение называют основным уравнением теории ценности. В координатной форме уравнение Слуцкого имеет вид:
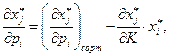
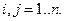 (2.7.6)
(2.7.6)
Левую часть этого уравнения называют общим эффектом (от влияния цены на спрос), первое слагаемое в правой части - влиянием замены (т.е. компенсированного изменения цены на спрос), второе слагаемое - влиянием дохода (влияние изменения дохода на спрос). Запишем уравнение в виде:
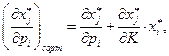
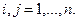 (2.7.7)
(2.7.7)
Из (2.7.4) следует, что матрица влияния замены симметрична и отрицательно определена. Из отрицательной определенности следует
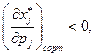
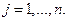 (2.7.8)
(2.7.8)
Следовательно, компенсированное возрастание цены товара приводит к уменьшению спроса на этот товар. Их симметричности матрицы влияния замены и уравнения (2.7.7) получаем:
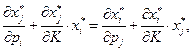
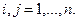
Поэтому из уравнения Слуцкого, в частности, следует, что:
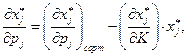
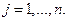 (2.7.9)
(2.7.9)
Производная 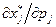 называется влиянием на спрос (на
называется влиянием на спрос (на 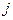 -й товар) изменения частной цены (цены
-й товар) изменения частной цены (цены 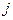 -го товара).
-го товара).
Равенство (2.7.9) используют для характеристики типов товаров.
Определение 2.4. Товар вида 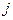 называется нормальным, если
называется нормальным, если 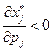 ; товаром Гиффина, если
; товаром Гиффина, если 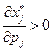 ; ценным, если
; ценным, если 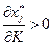 ; малоценным, если
; малоценным, если 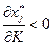 . Два товара
. Два товара 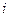 и
и 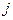 являются взаимозаменяемыми, если
являются взаимозаменяемыми, если 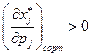 взаимодополняемыми, если
взаимодополняемыми, если 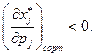
Из (2.7.8) и (2.7.9) следует
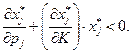
С учетом условия 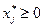 приходим к следующим выводам:
приходим к следующим выводам:
а) если 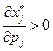 , то обязательно
, то обязательно 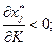
б) если 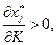 то обязательно
то обязательно 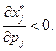
Отсюда следует, что товар Гиффина не может быть ценным, т.е. он обязательно малоценный. В общем случае каждый товар попадает в одну из следующих категорий.
1. Нормальный и ценный 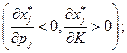
2. Нормальный и малоценный 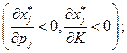
3. Товар Гиффина и малоценный 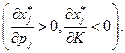
Существование товара Гиффина кажется не вполне реальным. Действительно, его определение противоречит закону о спросе (спрос есть убывающая функция цены). Однако когда какой-либо популярный среди населения товар продается по слишком низкой цене, появляется подозрение о его качестве. Это может оказаться причиной снижения спроса на него. Последующее же поднятие цены может повысить спрос на этот товар.
Нормальный и ценный товар отличается от нормального малоценного товара высоким качеством. Например, фрукты южных сортов по питательным и вкусовым качествам превосходят северные сорта, но они и дороже; масло дороже маргарина, так как качество его выше; вычислительная техника завода-изготовителя, как правило, качественнее и поэтому дороже, чем та же техника, но лицензионной сборки и т.д.). Умножая обе части равенства (2.7.4) на вектор 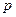 получим:
получим:
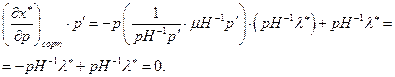
В координатной форме это равенство примет вид:
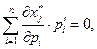
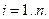 (2.7.10)
(2.7.10)
Учитывая положительность всех цен и неравенство (2.7.8) , приходим к выводу о том, что для каждого 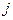 существует
существует 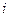
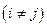 такое, что
такое, что
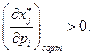
Таким образом, в наборе 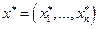 каждому товару соответствует по крайней мере один такой товар, который составляет с ним взаимозаменяемую пару.
каждому товару соответствует по крайней мере один такой товар, который составляет с ним взаимозаменяемую пару.
Из уравнения Слуцкого (2.7.5) и равенства (2.7.10) получаем
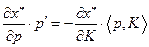
или
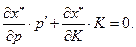
Запишем это равенство в координатной форме
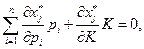
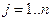
и разделим обе части каждого из 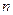 равенств на
равенств на 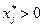 :
:
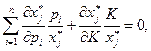
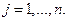
В обозначениях эластичности (см. (2.3.2) , (2.5.4)) имеем:
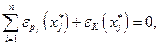
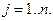
Отсюда следует вывод: для каждого товара 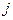 сумма всех
сумма всех 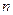 перекрестных эластичностей спроса по цене и эластичности спроса по доходу должна быть равна нулю, т.е. сумма всех эластичностей по цене равна отрицательной эластичности по доходу.
перекрестных эластичностей спроса по цене и эластичности спроса по доходу должна быть равна нулю, т.е. сумма всех эластичностей по цене равна отрицательной эластичности по доходу.
Умножая (2.7.2) на вектор цен 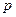 , получим
, получим
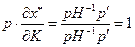
(условие агрегации Энгеля). В координатной форме:
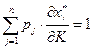 . (2.7.11)
. (2.7.11)
Отсюда следует неравенство 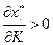 для некоторого
для некоторого 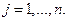 Следовательно, в наборе
Следовательно, в наборе 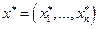 все товары одновременно не могут быть малоценными.
все товары одновременно не могут быть малоценными.
С учетом (2.7.10) и (2.7.11) из уравнения Слуцкого находим
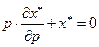
(условие агрегации Курно). В координатной форме:
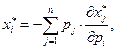
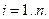
Отсюда следует вывод: значение спроса на товар вида 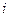 равно отрицательной взвешенной сумме изменений спроса на все товары по отношению к цене товара
равно отрицательной взвешенной сумме изменений спроса на все товары по отношению к цене товара 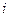 , в которой в качестве весов выступают цены товаров.
, в которой в качестве весов выступают цены товаров.
Исследуя уравнение Слуцкого можно получить и другие выводы по проблемам теории ценности и потребления.
Приведем геометрическую интерпретацию изложенных выше результатов для 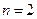 (Рис. 2.15). Пусть
(Рис. 2.15). Пусть 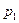 возрастает до
возрастает до 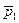 , а
, а 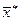 - решение задачи потребителя для параметров
- решение задачи потребителя для параметров 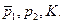 Тогда
Тогда 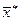 лежит в пересечении бюджетной линии, проходящей через точки
лежит в пересечении бюджетной линии, проходящей через точки 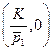 и
и 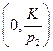 с кривой безразличия
с кривой безразличия 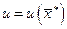 . Общий эффект
. Общий эффект 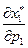 изменения
изменения 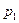 выражается отрезком
выражается отрезком 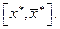
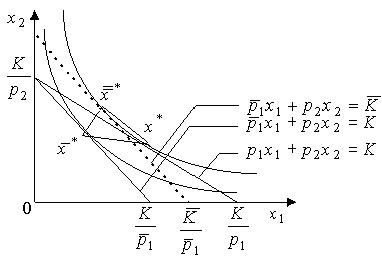
Рис. 2.15 Геометрическая иллюстрация уравнения Слуцкого
Точка 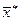 лежит левее
лежит левее 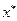 (т.к.
(т.к. 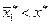 в силу
в силу 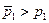 ), т.е. при возрастании цены первого товара спрос на него снизился. Следовательно, товар 1 нормален
), т.е. при возрастании цены первого товара спрос на него снизился. Следовательно, товар 1 нормален 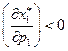 . Предположим теперь, что происходит компенсированное увеличение цены
. Предположим теперь, что происходит компенсированное увеличение цены 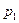 до
до 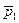 . Обозначим через
. Обозначим через 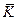 соответствующее компенсированное изменение (увеличение) дохода, т.е.
соответствующее компенсированное изменение (увеличение) дохода, т.е.
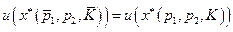 .
.
Геометрически бюджетная линия изменится (пройдет через 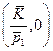 и
и 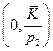 , а точка
, а точка 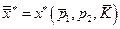 будет лежать в пересечении этой бюджетной линии с кривой безразличия
будет лежать в пересечении этой бюджетной линии с кривой безразличия 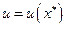 (по определению компенсированного изменения цены
(по определению компенсированного изменения цены 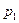 ).
).
Так как бюджетная линия 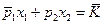 параллельна бюджетной линии
параллельна бюджетной линии 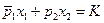 (имеет один и тот же тангенс угла наклона
(имеет один и тот же тангенс угла наклона 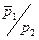 ), то точка
), то точка 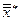 будет лежать левее точки
будет лежать левее точки 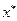 . Это подтверждение того, что влияние замены отрицательно. Влияние замены
. Это подтверждение того, что влияние замены отрицательно. Влияние замены 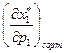 выражается отрезком
выражается отрезком 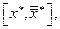 а влияние дохода
а влияние дохода 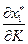 выражается отрезком
выражается отрезком 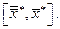 Точка
Точка 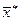 лежит левее точки
лежит левее точки 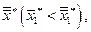 т.е. при возрастании дохода (от K до
т.е. при возрастании дохода (от K до 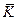 ) спрос на товар 1 увеличился. Следовательно, товар 1 является ценным
) спрос на товар 1 увеличился. Следовательно, товар 1 является ценным 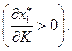
Дата добавления: 2015-11-28; просмотров: 2704;
