Поверки и юстировки электронных теодолитов
3.8 Способы измерения горизонтальных и вертикальных углов. Измерение горизонтальных углов проводится, как правило, способами приёмов и круговых приёмов. Способ приёмов заключается в следующем. Для измерения угла ВОА устанавливают теодолит над вершиной угла О. Вращением алидады наводят трубу на первую точку А (лимб закреплён). При закреплённой алидаде производят отсчёт по горизонтальному кругу. Открепив алидаду, наводят трубу на точку В и снова снимают отсчёт. Тогда величина угла равна разности отсчётов. Такое измерение углов называется полуприёмом. Для устранения влияния систематических погрешностей (коллимационной, неравенства колонок и т.п.) и для контроля угол измеряют при втором положении вертикального круга: переводят трубу через зенит, поворачивают алидаду на 180˚ и повторяют процедуру. Из полученных результатов вычисляют среднее значение угла. Такой способ измерения горизонтальных углов называется полным приёмом.
При измерении углов круговым способом поступают следующим образом. Установив теодолит над точкой О, и наведя трубу на первую точку, визируют все направления по ходу часовой стрелки и берут соответствующие отсчёты. Последнее визирование выполняют вновь на первую точку; если лимб был неподвижен, то первый и последний отсчёты должны совпасть, иначе необходимо произвести измерения заново. Далее вычисляют величины основных углов как разность отсчёта на данное направление и первого отсчёта. Во втором полуприёме переводят трубу через зенит и последовательно визируют те же направления, но уже против часовой стрелки. Все промежуточные углы вычисляются как разности основных углов.
Измерение вертикальных углов (углов наклона) производится при помощи вертикального круга теодолита. Для удобства измерений вертикальных углов необходимо, чтобы при горизонтальном положении визирной оси (и нахождении в нуль-пункте пузырька цилиндрического уровня при алидаде) отсчёт по вертикальному кругу был нулевым.

Рис. 12. Измерение вертикальных углов.
Однако это условие далеко не всегда выполняется. Отсчёт по вертикальному кругу, когда визирная ось горизонтальна, а пузырёк уровня при алидаде находится в нуль-пункте, называется местом нуля. Для измерения угла наклона зрительную трубу при положении КЛ наводят на некоторую точку A и, приведя пузырек в нуль-пункт, берут отсчёт Л. Аналогично берут отсчёт П. Тогда угол наклона (для теодолитов со шкалами вертикального круга с двойной оцифровкой, например, 4Т30) может быть найден как ν = Л – МО = МО – П, где место нуля МО = (Л+П)/2. Правильность измерения вертикальных углов контролируется постоянством МО (рис. 12). Точность измерения вертикальных углов зависит в первую очередь от погрешности отсчёта. Из других причин следует упомянуть вертикальную рефракцию (которую при длине менее 300 м можно не учитывать).
3.9 Источники погрешностей, влияющих на точность измерения углов и методы их ослабления. При измерении горизонтальных углов необходимо оценивать точность измерений. К систематическим погрешностям измерения горизонтальных углов относятся влияние наклона вертикальной оси, влияние эксцентриситета алидады (несовпадения центра лимба и центра алидады), влияние коллимационной погрешности (неперпендикулярности визирной оси и оси вращения зрительной трубы). Две последних погрешности устраняются при измерениях при двух положениях круга – полным приёмом.
Помимо вышеперечисленных, погрешности, возникающие при измерениях, могут быть классифицированы следующим образом: 1. погрешность визирования. 2. погрешность отсчитывания. 3. погрешность за центрирование. 4. погрешность за редуцирование.
Погрешность визирования (неточность наведения на цель) mv зависит от увеличения зрительной трубы v и для теодолита Т30 составляет около трёх секунд (mv = 60΄΄/v, где 60΄΄ - минимальный угол, при котором глаз наблюдателя различает две отдельные точки). Погрешность отсчитывания по штриховому микроскопу для того же теодолита составляет порядка 18΄΄ (исходя из формулы m0=0,03t, где t =10΄ - цена деления шкалы). Погрешность за центрирование (несовпадение центра прибора с вершиной угла) зависит от длины стороны хода и от погрешности mе (зависящей от точности центрирования) установки теодолита над вершиной измеряемого угла. Она вычисляется по формуле mx=(ρ/d)me, где ρ – коэффициент, равный 3437,75 (в минутах), а d – длина стороны теодолитного хода. Погрешность за редуцирование (несовпадение визирной цели с отвесной линией, проходящей через центр наблюдаемого пункта) аналогична погрешности за центрирование и при одинаковых условиях приблизительно с ней совпадает.
Линейные измерения
3.10 Непосредственный метод измерения. Мерные приборы. Измерение расстояний производят непосредственным или косвенным методом. При непосредственном измерении расстояния мерный прибор (рулетка, лента и т.п.) последовательно укладывают в створе измеряемого отрезка. При косвенном методе измеряют вспомогательные параметры (углы и базисы, время и т.п.), а длину находят по формулам, связывающим измеренные параметры и длину. Точность измерений в зависимости от метода колеблется в очень широких пределах (от 1:200 до 1:1000000). Закрепление концов отрезка в зависимости от назначения и сроков использования производится колышками, деревянными столбами, железобетонными монолитами. Для непосредственного измерения используют землемерные ленты со шпильками. Перед измерениями производят рекогносцировку, т.е. ознакомление с местностью. Затем выполняют вешение лини, т.е. установку вешек в створе линии. Измерение производят два человека: задний прикладывает ноль прибора к начальной точке и закрепляет ленту шпилькой, а передний, уложив ленту в створ, натягивает ленту и закрепляет её шпилькой. Далее ленту снимают, причём заднюю шпильку вынимают. Операцию повторяют. Когда у переднего рабочего заканчиваются шпильки, задний передаёт ему 10 штук; передача отмечается в журнале. Остаток r измеряют по надписям на пластинках (целое число метров), по отверстиям (расположенным через дециметр) и сантиметры – на глаз. Длина линии вычисляется по формуле D = nl + r, где n – число целых отложений ленты, l – длина ленты. Все линии измеряют в прямом и обратном направлениях, за окончательное значение принимают среднее из них.


Рис. 13. Определение неприступного расстояния.
Встречаются случаи, когда при измерении длины линии мерную ленту применить невозможно, а дальномер отсутствует или его использование невозможно. Тогда неизвестное расстояние l вычисляют, измерив длину базиса b и углы α и β (рис.13), при этом желательно измерить угол γ. Тогда по теореме синусов l = sinβ/sinγ×b. Если угол γ измерить невозможно, то γ = 180º – (α + β). Углы α и β должны быть близки к 60º.
3.11 Компарирование мерных приборов. Под влияние различных факторов длина мерного прибора изменяется. Поэтому перед началом и в конце сезона мерные приборы компарируют, т.е. определяют их фактическую длину. Для этого производят сравнение длин прибора и эталона или базиса. Если длина прибора и эталона одинакова, то проводят непосредственное сравнение их длин; тогда длина прибора
l = l0 + δlк,
где δlк – поправка за компарирование. В полевых условиях компарирование выполняют на базисах (как правило, длиной 120 м). После многократных измерений длины компаратора Dк мерным прибором поправку за компарирование вычисляют по формуле
δlк = (Dк – Dр)/n,
где n = Dр/l0 – число отложений мерного прибора.
3.12 Вычисление длин линий. При вычислении длин линий в результат вводятся некоторые поправки. Поправка в длину мерного прибора за компарирование δDк = (D0/l0)/δlк. Поправка в длину мерного прибора за температуру δDt = α(t – t0)D0 , где α – коэффициент линейного расширения материала мерного прибора, а t0 – температура, при которой проводилось компарирование, вводится в том случае, если разность температур, при которых проводились измерения и компарирование, превышает 8º. При высокоточных измерениях на конструкциях уникальных сооружений водятся дополнительные поправки за температуру конструкций. Поправка за приведение линии к горизонту может быть вычислена как
δDν = – 2Dsin2 (ν/2) или δDν = – ½ sin2 ν (при ν<10º),
где ν – угол наклона, или
δDh = –h2/2D,
где h – превышение концов измеряемой линии. Поправка за приведение линии к горизонту учитывается, как правило, в том случае, если угол наклона более 3º.
3.13 Источники погрешностей, влияющих на точность линейных измерений. На точность измерения линий влияют как систематические, так и случайные погрешности. Помимо вышеупомянутых поправок, рассматривают также погрешности за компарирование (её принимают равной λк = 0,6 мм), погрешность за уложение мерного прибора в створ (λc = m2c/(l√2), погрешность за превышение концов мерного прибора (λh = m2h/2l , где mh – средняя квадратическая погрешность измерения превышения). Из случайных погрешностей рассматриваются: погрешность отсчитывания по шкалам мерного прибора η0,1 = 0,15τ; погрешность фиксации концов мерного прибора ηф = 1,5 мм для фиксации шпильками и ηф = 1,0 мм при прочерчивании линии на асфальте карандашом. Также рассматриваются погрешности при измерении параметров систематических погрешностей. Требования к точности линейных измерений зависят от характеристик сооружения и вида конструкции. Условия, необходимые для обеспечения заданных точностей, даны в СНиП.
3.14 Косвенные измерения.Нитяной дальномер. Свето- и радиодальномеры. Лазерный дальномер. Методика измерений, точность измерений и поправки в результаты измерений. Нитяной дальномер – это дальномер с постоянным параллактическим углом и переменным базисом. Принцип его работы основан на решении прямоугольного треугольника: по известному малу параллактическому углу и катету (базису) определяют расстояние (гипотенузу). Для измерения расстояний на одном конце отрезка устанавливают рейку, на другом – прибор. Наведя прибор на рейку и взяв отсчёты по дальномерным нитям, вычисляют длину базиса n (разность отсчётов по нитям). Если визирный луч не горизонтален, то отсчёт по рейке увеличится на величину 1/cos ν, где ν – угол наклона, следовательно отсчёт надо умножить на cos ν. Тогда расстояние будет равно произведению исправленного отсчёта на величину K, называемую коэффициент дальномера. В современных приборах он, как правило, равен 100. Полученная величина – длина наклонной линии; горизонтальное проложение, т.о., может быть найдено как
l = Kn cos2 ν.
Относительная погрешность измерения расстояний нитяным дальномером колеблется от 1:200 до 1:400.
Принцип действия электромагнитного дальномера основан на измерении времени прохождения сигналом измеряемого расстояния. Общая схема такова: на одной из точек устанавливают приёмопередатчик, на другой – отражатель. Измерив время между излучением сигнала и его приходом обратно τ2D, и зная скорость распространения сигнала v можно по формуле D = vτ2D/2 определить расстояние. При измерении временного интервала непосредственно возникают большие трудности, поэтому обычно измеряют через функцию от времени. Основным методом является фазовый. Фазоизмерительное устройство определяет разность фаз излучаемого и принимаемого колебания. Тогда время прохождения сигнала будет
τ2D = Δφ2D/2πf,
и, соответственно, расстояние
D = vτ2D/2 = vΔφ2D/4πf .
Однако в действительности, т.к. Δφ2D = 2πN + φ и фазоизмерительное устройство может измерить разность фаз от 0 до 2π, то, переписав формулу в виде D = (N + ΔN)/λ2 замечаем, что мы не знаем величины N, т.е. возникает т.н. неоднозначность в значении измеряемого расстояния. Для разрешения неоднозначности используют способ плавных частот и способ фиксированных частот. Пусть мы плавно меняем частоту f, и, следовательно, длину волны λ, до тех пор, пока дробная часть периода не станет равна нулю. Тогда D = Nc/2f1. При дальнейшем изменении частоты вновь возникшая дробная часть снова попадёт: D = (N+1)c/2f2, и т.д. вплоть до D = (N+n)c/2fn. Тогда N = nf1/(fn – f1). Описанный метод применяют в дальномерах с переменной частотой модуляции. В случае использования метода фиксированных частот получают систему уравнений вида D = (N1 + ΔN1)λ1/2, D = (N2 + ΔN2)λ2/2, D = (N3 + ΔN3)λ3/2 и т.д. На практике отношения частот берут равным 10; это позволяет определять расстояния с точностью до 1000, 100, 10 и т.д. метров. Точное значение расстояния получают по частоте f1, все остальные частоты используют для разрешения неоднозначностей.
Нивелирование
3.15 Виды нивелирования. Нивелирование – это вид полевых геодезических работ по определению высот точек и превышений между ними. Нивелирование используют для определения высот точек; при производстве строительно-монтажных работ с помощью нивелирования устанавливают строительные конструкции в проектное положение по высоте. Различают нивелирование геометрическое, тригонометрическое, физическое, стереофотограмметрическое и автоматическое.

3.16 Приборы для нивелирования. Геометрическое нивелирование выполняется при помощи нивелиров и нивелирных реек. Нивелиры, в зависимости от их конструкции, бывают с цилиндрическим уровнем или с компенсатором (с самоустанавливающейся линией визирования). Нивелиры в соответствии с их точностью делятся на высокоточные, точные и технические.
| Наименование параметра | Нивелиры | ||
| высокоточные | точные | технические | |
| Допустимая средняя квадратическая погрешность измерения превышения на 1 км двойного хода, мм: | |||
| для нивелиров с компенсатором | 0,3 | 2,0 | 5,0 |
| для нивелиров с уровнем | 0,5 | 3,0 | - |
| Увеличение зрительной трубы, крат, не менее |
Основные технические параметры нивелиров.
Основными частями нивелира с цилиндрическим уровнем являются: подставка с подъёмными винтами, зрительная труба, круглый уровень, цилиндрический уровень. Его основными осями являются ось вращения прибора, визирная ось зрительной трубы, ось цилиндрического уровня. У нивелира с компенсатором цилиндрический уровень отсутствует. Уровень или компенсатор служат для приведения визирной оси в горизонтальное положение; при наличии компенсатора визирная ось устанавливается в горизонтальное положение автоматически в пределах угла компенсации. При измерении превышений по рейке берут отсчёт – расстояние от пятки рейки до визирной оси. Это расстояние измеряют в миллиметрах. Существует два способа нивелирования – вперёд и из середины; на практике преимущественно используется второй способ. Он заключается в следующем. Нивелир устанавливают посередине между рейками, установленными на точках. Створность расположения прибора не столь важна, гораздо более важным является условие равенства плеч – равенства расстояний от прибора до реек. Сняв отсчёты по задней ν2 и передней ν1 рейкам, находят превышение h = ν2 – ν1.

Рис. 14. Оптический нивелир 3Н5Л. Увеличение – 20˟, средняя квадратическая погрешность измерения превышений – 4 мм на километр двойного хода.
Нивелиры делят на высокоточные, точные и технические. У высокоточных нивелиров погрешность не более 0,5 мм на 1 км двойного хода. К точным относят нивелиры с погрешностью не более 3 мм на 1 км двойного хода. Техническими считаются нивелиры, обеспечивающие точность до 10 мм на 1 км двойного хода. Помимо оптических нивелиров с уровнем и компенсатором в последнее время широкое применение нашли цифровые нивелиры, которые осуществляют автоматическое отсчитывание по рейке со штрих-кодом BAR (рис. 17) или RAB (рис. 16), что позволяет избежать личных погрешностей наблюдателя.

Рис. 15. Нивелирная рейка РН – 3000У.

Рис. 16. Нивелирная рейка BGS 40 с RAB-кодом (4 метра, три секции).

Рис. 17. Нивелирная рейка LD 11 с BAR-кодом (1 метр).
Нивелирные рейки бывают односторонними, когда деления нанесены на одной стороне, и двусторонними. У двусторонних реек (например, РН-3000У, рис. 15) на одной стороне нанесены деления чередующихся белого и чёрного цвета (чёрная сторона), на другой – красного и белого (красная сторона). На чёрных сторонах отсчёт начинается с нуля; на красных – с любого некруглого числа, не встречающегося на чёрной стороне (как правило, с 4687 или 4787 мм). При снятии отсчёта по красной и чёрной сторонам разность отсчётов должна быть равна тому числу, с которого начинается счёт на красной стороне – разности пяток. При высокоточных измерениях (при развитии государственных сетей и наблюдениями за деформациями зданий и сооружений) применяются инварные рейки, используемые совместно только с высокоточными нивелирами (рис.18).

Рис. 18. Инварная нивелирная рейка 391189 прямого изображения с постоянным натяжением инварной полосы 10 кг («NEDO», Германия)
3.17 Поверки и юстировки нивелиров. До начала работы с прибором необходимо убедиться в его исправности. Для этого сначала производят внешний осмотр: проверяют наличие и исправность всех частей, плавность хода винтов, чёткость изображения. Затем приводят прибор в рабочее положение: вращением подъёмных винтов приводят пузырёк круглого уровня в нуль-пункт. Для нивелира с цилиндрическим уровнем его пузырёк приводят в нуль-пункт вращением элевационного винта после наведения на рейку. Это осуществляется путём совмещения изображений концов пузырька в поле зрения трубы. После приведения в рабочее положение у нивелиров с цилиндрическим уровнем и с компенсатором проводят поверки следующих условий.
1. Ось круглого уровня должна быть параллельна оси вращения прибора. Вращением трёх подъёмных винтов приводят пузырёк круглого уровня в нуль-пункт. При повороте прибора на 180º пузырёк должен оставаться в нуль-пункте. В противном случае подъёмными винтами смещают пузырёк в сторону нуль-пункта на половину отклонения, а затем юстировочными (исправительными) винтами приводят его в нуль-пункт. Поверку (при необходимости – юстировку) повторяют.
2. Горизонтальная нить сетки нитей должна быть горизонтальна, вертикальная – вертикальна. А рейке, отстоящей на 5-10 м от прибора, берут отсчёты по правому и левому краям нити. Если они равны, то условие выполнено, в противном случае сетку нитей поворачивают исправительными винтами до получения равных отсчётов.
3. Параллельность визирной оси и оси цилиндрического уровня (для нивелира с уровнем) или горизонтальность визирной оси (для нивелиров с компенсатором) устанавливают одним из двух способов. Первый способ – двойным нивелированием. Установив нивелир на одной из точек, измеряют высоту прибора i1 и берут отсчёт по рейке на второй точке v1, отстоящей на 50-70 м (рис. 19). Этот отсчёт больше истинного на величину x, т.е. превышение h = i1 – (v1 – x) = i1 – v1 + x. Поменяв местами рейку и нивелир, повторяют измерения. Тогда h = v2 – x – i2. отсюда x = (v1 + v2)/2 – (i1 + i2)/2. Если эта величина не превышает 4 мм (что соответствует расхождению осей менее 10′′), то условие считают выполненным. Второй способ – нивелированием из середины и вперёд. Из точки, равноотстоящей от концов отрезка, берутся отсчёты n1 и v1 по рейкам (рис. 20). Отклонение y, вызванное непараллельностью осей, в силу равенства расстояний, одинаково, поэтому, пользуясь формулой h = n1 – y – (v1 – y) = n1 – v1, получают правильное значение превышения. Далее, перенеся нивелир за одну из реек и измерив его высоту i2, предвычисляют отсчёт по второй рейке: v = i2 – h. Если предвычисленный отсчёт совпадает с действительным или отличается от него на величину x, не превышающую по модулю 4 мм, то условие считают выполненным. (При необходимости можно вычислить и угловую величину погрешности i = x/d×ρ). В случае, если величина x больше 4 мм, визирную ось устанавливают на предвычисленный отсчёт v и, действуя вертикальными исправительными винтами уровня, совмещают концы пузырька.




Рис. 19. Поверка главного условия методом двойного нивелирования вперёд


Рис. 20. Поверка главного условия нивелированием из середины и вперёд.
3.18 Источники погрешностей при геометрическом нивелировании. На каждой станции геометрического нивелирования превышения определяют по черной и красной сторонам рейки, за окончательное значение принимают среднее арифметическое. Основными погрешностями, влияющими на точность измерений, являются следующие. Погрешность за кривизну Земли – систематическая погрешность, её величина приближённо равна k = d2/2R, где d – расстояние от нивелира до рейки, R – радиус Земли. Поправка за вертикальную рефракцию равна r = d2/2Ra, где Ra – радиус рефракционной кривой. При нивелировании из середины в случае равенства расстояний от нивелира до точек поправки за кривизну Земли и за рефракцию (с некоторыми оговорками) можно не учитывать. Погрешность за негоризонтальность визирного луча и неравенство плеч λГУ (нарушение главного условия) при наибольших допускаемых значениях отклонения осей i = 10′′ и разности плеч d = 10 м равна λГУ = (10/206265)•104 = 0,5 мм. К случайным погрешностям относятся погрешность отсчёта по шкале рейки, погрешность совмещения изображения концов пузырька цилиндрического уровня, погрешность делений рейки и т.д.
3.19 Техническое нивелирование. Нивелирование IV класса. Для определения высот точек на стройплощадках в основном применяют техническое нивелирование; при этом используются нивелиры Н-10, Н-3. При техническом нивелировании работу на станции выполняют в следующем порядке. На крайние точки устанавливают рейки, на равном удалении от них – нивелир; неравенство плеч не превышает 10 м. Нивелир приводят в рабочее положение. Берут отсчёт по чёрной стороне задней рейки, потом – по чёрной передней, по красной передней и по красной задней. Для контроля вычисляют разность нулей передней и задней реек; расхождение разностей не должно превышать 5 мм. Определяют превышения по чёрным и красным сторонам; превышения считают определёнными верно, если разность между превышением, вычисленным по черной стороне, не отличается от превышения, вычисленного по красной, более чем на 5 мм. При техническом нивелировании разность расстояние от нивелира до реек не должна превышать 120 м. Для создания высотного обоснования используют нивелирование IV класса; оно проводится при помощи нивелиров Н-3. Порядок работы при нивелировании IV класса такой же, как и при техническом нивелировании. Расстояния до реек определяют нитяным дальномером и разность плеч не должна превышать 5 м. При наблюдениях за осадками и деформациями зданий и сооружений, выверке технологического оборудования используют метод нивелирования короткими лучами: для повышения точности определения превышений ограничиваются расстояниями, не превышающими 50 м. Измерения производят нивелирами Н-05.
3.20 Тригонометрическое нивелирование. При тригонометрическом нивелировании над первой точкой устанавливают теодолит и измеряют его высоту ιп, а на второй точке устанавливают рейку. Для определения превышения h измеряют угол наклона ν, горизонтальное проложение d и высоту визирования (отсчёт по рейке) k. Тогда h = d tgν + ιп – k. При топографических съёмках расстояние измеряют при помощи нитяного дальномера, т.е. d = (Kn + c) cos2 ν. При проведении съёмок, как правило, визирный луч наводят на отметку на рейке, расположенную на высоте прибора, т.е. ιп = k. Пренебрегая с, получим окончательно:
h = ½ Knsin2ν.
Глава IV
Геодезические сети
4.1 Основные сведения о геодезических сетях и методах их создания. При проведении ряда народнохозяйственных мероприятий требуются топографические карты и планы, составленные на основе сети геодезических пунктов, чьё плановое (высотное) положение известно в единой системе координат (высот). Построенная на большой территории (согласно составленному для неё проекту) в единой системе координат и высот сеть позволяет: правильно организовывать работу по съёмке местности; строить единые карты по измерениям, проведённым в разных местах в разное время; равномерно распределять по территории влияние погрешностей измерений. Геодезические сети строят по принципу от общего к частному. Вначале строится редкая сеть с высокой точностью, а затем эту сеть последовательно по ступеням сгущают пунктами, которые строят от ступени к ступени всё с более низкой точностью. Сеть стараются сгущать таким образом, чтобы получать равномерную плотность пунктов на местности. Плановые геодезические сети строят методами триангуляции, полигонометрии, трилатерации и их комбинациями. Метод триангуляции состоит в построении сети треугольников, в которых измеряются все углы, а также как минимум две стороны на разных концах сети. По длине одной стороны и углам определяют все стороны треугольников. Зная координаты одного из пунктов и дирекционный угол одной из линий, можно вычислить координаты всех пунктов. Метод полигонометрии заключается в построении на местности ходов, в которых измеряются все стороны и все углы. Метод трилатерации состоит в построении сети треугольников, в которых измеряют все стороны.
4.2 Государственные сети, геодезические сети сгущения и съёмочное геодезическое обоснование. Плановые геодезические сети делятся на государственную геодезическую сеть, разрядные сети и съёмочное обоснование. Государственная геодезическая сеть представляет собой совокупность геодезических пунктов, равномерно распределённых на территории страны и закреплённых на местности центрами, обеспечивающими их сохранность. Государственную геодезическую сеть (согласно Основным положениям о построении государственной геодезической сети СССР, 1954 г.) подразделяют на триангуляцию, полигонометрию и трилатерацию 1, 2, 3 и 4 классов и нивелирные сети I, II, III и IV классов. В первую очередь строят триангуляцию 1-го класса в виде рядов треугольников; эти ряды расположены по возможности вдоль меридианов и параллелей, длины сторон треугольников не менее 20 км, периметр полигонов, образуемых рядами треугольников – около 800 км. На пересечении рядов треугольников определяют длины выходных (базисных) сторон. На концах этих сторон из астрономических наблюдений определяют широту, долготу и азимут. Триангуляцию 2-го класса строят в виде системы треугольников, сплошь заполняющей полигоны сети 1-го класса (рис. 21). Внутри сети 2-го класса выбирают базисную сторону, определяют её длину и азимут, а также широту и долготу её концов. Так как при построении этих сетей используются астрономические наблюдения, их называют астрономо-геодезическими сетями.
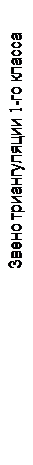


Рис. 21. Схема построения плановой государственной сети методом триангуляции
На местности пункты закрепляются заглублёнными в землю центрами в виде бетонных, кирпичных, каменных сооружений, железобетонных пилонов и т.д. Типы центров установлены соответствующими инструкциями. Над центрами сооружают наружные знаки, которые служат визирными целями. Высотные геодезические сети создают в основном методами геометрического и тригонометрического нивелирования и подразделяют на государственную нивелирную сеть и сети технического нивелирования. Государственная нивелирная сеть обеспечивает высотной основой, упорядочивает связи уровней внешних морей с высотной сетью. Она позволяет исследовать (повторным нивелированием) вертикальные деформации земной коры. Государственная нивелирная сеть состоит из сетей I, II, III и IV классов. Нивелирные линии I класса прокладываются по направлениям, связывающим удалённые друг от друга пункты и основные морские водомерные посты. Нивелирная сеть II класса опирается на пункты I класса. Периметры полигонов нивелирования I и II классов в среднем составляют 2800 и 600 км соответственно. Нивелирные сети III класса образуют полигоны с периметром 150 км. Для обеспечения съёмки в масштабах не мельче 1:5000 периметр не должен превышать 60 км. Длина ходов IV класса не превышает 50 км. Пункты этих ходов являются высотным обоснованием топографических съёмок.
4.3 Обозначение пунктов государственной геодезической сети на местности.Геодезические пункты закрепляются на земной поверхности геодезическими центрами, представляющими собой железобетонные монолиты, закладываемые ниже глубины сезонного промерзания. Над центрами государственных плановых сетей 1-4 классов устанавливают наружные знаки различных конструкций (рис. 22). Основное их назначение – поднять визирную марку и геодезический прибор на высоту и произвести измерения на находящиеся в зоне прямой видимости соседние знаки.
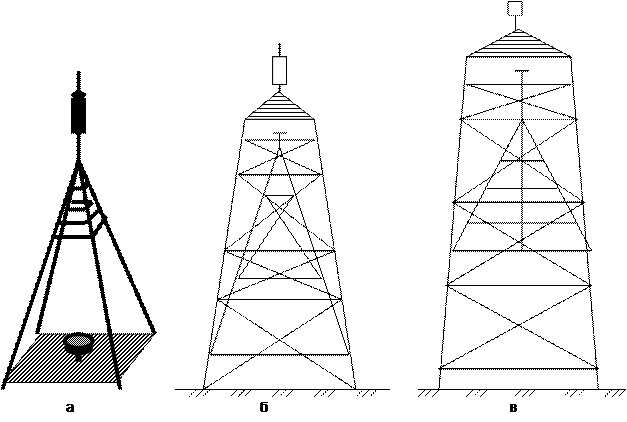
Рис. 22. Наружные геодезические знаки: а – пирамида, б – простой сигнал, в – сложный сигнал.
Пункты высотной государственной сети закрепляют на местности капитальными грунтовыми реперами, стенными реперами или марками. На всех нивелирных сетях I и II класса капитальные реперы (рис. 23) закладывают на устойчивых геологических породах через 50-80 км. Нивелирные сети III и IV класса закрепляют стандартными реперами и марками в среднем через 7-8 км.

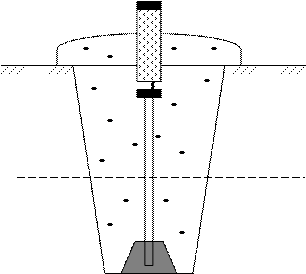
Рис. 23. Капитальный грунтовый репер государственной нивелирной сети.
Координаты и высоты пунктов государственных геодезических сетей приводятся раздельно в каталогах координат или каталогах высот геодезических пунктов. Каталоги содержат описание физико-географических условий, год производства работ, схему обоснования, анализ и оценку точности произведённых работ. Каталоги хранятся в Госгеокартофонде, в подразделениях ГУГК РФ, Госгеонадзоре, районных админстрацях.
4.4 Современное состояние и структура государственной геодезической сети. Современное состояние государственной геодезической сети (ГГС) определено в Основных положениях о государственной геодезической сети, 2000 г. ГГС в настоящее время включает в себя астрономо-геодезическую сеть (более 160 тыс. пунктов), геодезические сети сгущения (около 300 тыс. пунктов) и спутниковые сети – космическую геодезическую сеть (26 пунктов) и доплеровскую геодезическую сеть (131 пункт). ГГС охватывает всю территорию России. Пункты различных сетей совмещены или имеют надёжные геодезические связи.
Постановлением Правительства Российской Федерации от 28.07.2000 г. «Об установлении единых государственных систем координат» установлена единая государственная система геодезических координат 1995 г. (СК-95). СК-95 получена по результатам двух этапов уравнивания: по совместному уравниванию АГС, ДГС и КГС определена сеть из 134 пунктов со средним расстоянием между пунктами 400…500 км; через год при окончательном уравнивании АГС сеть была использована в качестве жёсткой основы. За отсчётную поверхность принят референц-эллипсоид Красовского. Положение пунктов в СК-95 задаётся пространственными прямоугольными координатами, геодезическими координатами и плоскими прямоугольными координатами, вычисленными в проекции Гаусса-Крюгера.
Основными положениями о государственной геодезической сети предусмотрено создание новой структуры ГГС в виде фундаментальной астрономо-геодезической сети, высокоточной геодезической сети, спутниковой геодезической сети I класса, астрономо-геодезической сети, геодезической сети сгущения. ФАГС практически реализует общеземную геоцентрическую систему координат; расстояния между её (периодически обновляемыми) пунктами 800 … 1000 км. Пространственное положение пунктов определяют методами космической геодезии с точностью в плане 2 см и по высоте 3 см. Взаимное положение пунктов ВГС определено с точностью 3 мм+5•10-8D (D – расстояние между пунктами в мм) по каждой плановой координате и 7 мм+5•10-8D по геодезической высоте. Каждый пункт ВГС связан со смежными пунктами ВГС и не менее чем с тремя пунктами ФАГС.
На основе государственной геодезической сети строят разрядные сети сгущения, которые используют при создании съёмочного обоснования. Плановые сети сгущения создают теми же методами, что и государственную сеть. Разрядные сети сгущения разделяют на 1-ый и 2-ой разряды; триангуляцию развивают в виде сетей и отдельных пунктов. Пункты сети сгущения закрепляют на местности подземными знаками, на пунктах триангуляции 1-го и 2-го разрядов устанавливают наружные знаки – пирамиды и вехи (вехи ставят с северной стороны от центра). Высотные сети сгущения создают в основном проложением ходов технического нивелирования между пунктами государственной нивелирной сети. Съёмочные сети являются непосредственным геодезическим обоснованием топографических съёмок.
4.5 Теодолитный и нивелирный ходы. Полевые работы и камеральная обработка. Теодолитные ходы создаются методом полигонометрии. Геодезическая сеть в этом случае создаётся в виде системы замкнутых или разомкнутых ломаных линий, в которых непосредственно измерены все элементы – углы и длины сторон. Углы в полигонометрии измеряют точными теодолитами, стороны – светодальномерами или мерными проволоками. Если в ходе углы измерены техническим теодолитом, а длины – стальной землемерной лентой, то этот ход называют теодолитным. Теодолитные ходы бывают замкнутыми и разомкнутыми (опирающимися на две твёрдые стороны). Полевые работы при прокладке теодолитного хода следующие. 1. Рекогносцировка участка (выбор положения вершин хода и привязка к опорной сети). 2. Измерение углов (полным приёмом). 3. Измерение длин сторон. Камеральная обработка теодолитного хода заключается в следующем. В качестве исходных данных используют дирекционные углы начальной и конечной опорных сторон, координаты начальной и конечной точек хода. При вычислении координат всех точек хода сначала вычисляют дирекционные углы конечных линий. Для этого для правого хода, т.е. хода, в котором измерялись правые относительно сторон углы, пользуются формулой αi = αi-1 + 180º – βi., а для левого – αi = αi-1 – 180º + βi. Вычисленный таким образом дирекционный угол второй опорной стороны из-за погрешностей измерений будет отличаться от исходного – появляется невязка (разность теоретического и практического значений). По величине невязки судят о точности измерений; если невязка меньше предельно допустимой, то её распределяют на все углы поровну с обратным знаком и получают исправленные углы. По исправленным углам вычисляют дирекционные углы всех сторон хода. По полученным углам и длинам сторон вычисляют приращения координат: Δxi = di cosαi, Δy = di sinαi. Зная координаты начальной точки, можно вычислить координаты всех остальных. Здесь также возникают невязки приращений координат – разности между суммами приращений и разностями координат конечных точек. Невязки распределяют пропорционально длинам сторон (поправки определяют как δxi = -fx di /P, δyi = -fy di /P, где P – длина хода).
Нивелирные ходы прокладывают для определения высот точек съёмочного обоснования. При создании высотного обоснования нивелирный ход прокладывают, как правило, по точкам планового обоснования. В поле выполняют рекогносцировку, измерение превышений между соседними точками хода (геометрическим нивелированием). При вычислительной обработке результатов измерений вычисляют высоты точек. Разность между вычисленной отметкой конечной точки и её фактическим значением называется невязкой хода. Распределяют невязку нивелирного хода поровну.
Глава V
Дата добавления: 2015-12-26; просмотров: 4295;
