Системы координат, используемых в геодезии.

В инженерной геодезии наиболее часто используются системы географических, прямоугольных и полярных координат.В системе географических координат за координатную поверхность принимается шар, а за координатные линии – географические (истинные) меридианы и параллели. Сечения поверхности шара плоскостями, проходящими через полярную ось вращения Земли, называют меридианами. Сечения поверхности шара плоскостями, перпендикулярными оси вращения Земли, называют параллелями. Параллель, плоскость которой проходит через центр Земли, называют экватором. Положение точки на шаре определяется пересечением меридиана и параллели, проходящих через эту точку. Меридиан задаётся географической долготой точки, а параллель – географической широтой. Географической широтой φ точки называют угол между отвесной линией в точке и плоскостью экватора. Географической долготой точки называют угол λ между плоскостью меридиана точки и плоскостью Гринвичского меридиана. В системе геодезических координат геодезическая долгота совпадает с географической; геодезическая широта – угол между нормалью к эллипсоиду и плоскостью меридиана.

Рис. 2. Система геодезических координат.

Система плоских прямоугольных координат применяется на сравнительно небольших участках земной поверхности, принимаемых за плоскость. Основными координатными линиями служат две взаимно перпендикулярные линии. У вертикальной оси абсцисс Х, совмещённой с меридианом, положительное направление с юга на север, у горизонтальной оси ординат Y положительное направление – с запада на восток. Систему полярных координат применяют для определения планового положения точек на небольших участках в процессе съёмки местности и при геодезических разбивочных работах. За начало координат - полюс принимают точку местности, за начальную координатную линию – полярную ось, произвольно расположенную на местности. Полярными координатами точки будут полярный угол, отчитываемый по часовой стрелке от полярной оси и полярное расстояние (радиус-вектор).

Систему плоских прямоугольных координат Гаусса-Крюгера используют при крупномасштабном изображении значительных частей земной поверхности на плоскости. Система координат обладает особенностями, зависящими от выбранной проекции, т.е. метода отображения земной поверхности на плоскость. Для крупномасштабного картографирования необходима проекция, обеспечивающая сохранение подобного изображения фигур при переходе с поверхности шара на плоскость, возникающие при этом искажения размеров фигур должны быть малы и легко учитываться. Данным требованиям отвечает поперечно-цилиндрическая равноугольная проекция Гаусса-Крюгера. Изображение поверхности земного шара на плоскости в проекции Гаусса-Крюгера получают следующим образом (рис. 3). Поверхность разбивают меридианами на зоны шириной 3° или 6° по долготе. Земной шар вписывают в цилиндр так, чтобы плоскость экватора совместилась с осью цилиндра. Каждая зона из центра Земли проектируется на боковую поверхность цилиндра. После проектирования боковую поверхность цилиндра разворачивают в плоскость, разрезав её по образующим, проходящим через полюса. На полученном изображении средние (осевые) меридианы зон и экватор – прямые линии, остальные меридиана и параллели – кривые линии.

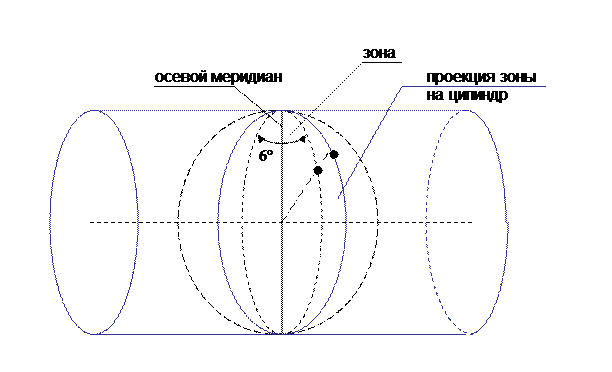Рис. 3. Поперечная цилиндрическая проекция Гаусса-Крюгера.

Искажения размеров контуров вблизи средних (осевых) меридианов зон минимальны и возрастают по мере удаления к краям. Линия на поверхности шара длиной S при изображении её на плоскости получит искажение

ΔS = y_m²S/2R,

где y_m = (y₁ + y₂)/2 – среднее значение из ординат начальной и конечной точек линии, R – радиус Земли. Относительные искажения ΔS/S на краях шестиградусной зоны могут достигать величины порядка 1/1500, а трёхградусной – порядка 1/6000. Выбор ширины зоны зависит от того, с какой точностью должно вестись проектирование строительного комплекса. Если для проектирования нужны топографические материалы масштаба 1:10000 и мельче, применяют шестиградусные зоны, для более крупных масштабов – трёхградусные. За начало отсчёта координат в каждой зоне принимают точку пересечения осевого меридиана - оси абсцисс Х и экватора – оси ординат Y. На картах проводят прямоугольную координатную сетку, состоящую из прямых линий, параллельных осевому меридиану и экватору. Расстояния между смежными линиями сетки составляют для масштаба 1:10000, 1:25000 и 1:50000 один километр на местности. Система координат в каждой зоне одинаковая. Для территории России, расположенной в северном полушарии, абсциссы всегда положительны. Для того, чтобы и ординаты были всегда положительны, начало координат смещают на запад на 500 км (тогда все ординаты будут больше 100 и меньше 1000 км, т.е. будут выражаться трёхзначным числом в километрах). В этом случае все точки к востоку и западу от осевого меридиана будут иметь положительные ординаты. Такие ординаты называются преобразованными. Преобразованная ордината начинается с номера зоны. Например, если точка расположена в шестнадцатой зоне в 54 345 м к западу от осевого меридиана, то её преобразованная ордината равна 16 445 655 м, если же она лежит на том же расстоянии к востоку, то её преобразованная ордината равна 16 554 345 м.

1.5 Системы высот.Для определения положения точек физической поверхности Земли недостаточно знать только две их плановые координаты. Необходима третья координата, характеризующая расстояние по отвесной линии от точки земной поверхности до начальной поверхности. Расстояние по отвесной линии от точки земной поверхности до начальной поверхности называют высотой. За начальную (отсчётную) поверхность для определения высот в геодезии принимается основная уровенная поверхность – поверхность геоида, называемая также уровнем моря. Такие высоты называются абсолютными. В РФ за начало отсчёта абсолютных высот принята уровенная поверхность, совпадающая со средним уровнем Балтийского моря; эту систему высот называют Балтийской. Если за начальную поверхность принимают произвольную уровенную поверхность, то такие высоты называют относительными. В строительстве применяют относительную систему высот; за отсчётную поверхность принимают уровенную поверхность, совпадающую с полом первого этажа жилого дома или полом цеха промышленного предприятия. Такую поверхность называют уровнем чистого пола, а высоты, отсчитываемые от него, - условными (рис. 4). Численное значение высоты называют отметкой. Разность высот двух точек называют превышением. Если рассмотреть линию АВ, то при превышении h точки А над В превышением В над А будет –h.

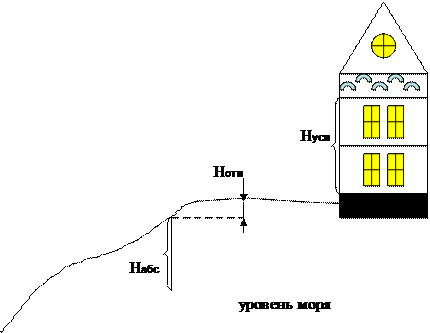
Рис. 4. Абсолютная, относительная и условная высоты.