Геодезические измерения

3.1 В повседневной деятельности постоянно приходится сталкиваться с необходимостью измерений. В случае «штучности» объектов достаточно простого счёта, иначе необходимо сравнение с некоторыми заранее определёнными величинами. Такой процесс сравнения называют измерением. Результат измерения – число; таким образом объект получает количественную характеристику.

Единицы мер. При геодезических измерениях пользуются в основном линейными и угловыми мерами. Расстояния в геодезии измеряют в метрах, углы – в градусах. За единицу площади берут квадрат со стороной, равной единице длины, за единицу объёма – куб с соответствующей стороной. Следует помнить, что 1 гектар – это 10^-2 км², 100 ар (10⁴ м²). Углы измеряются в градусах (1 градус – центральный угол с дуговым градусом в 1/360 окружности), минутах (1/60 градуса) и секундах (1/60 минуты). Иногда углы задаются в радианах, тогда для перехода следует помнить, что 1 радиан – это 206265 секунд. Иногда прямой угол делят на сто частей – гонов. Каждый гон делится на 100 десятичных минут, каждая минута – на 100 десятичных секунд. Тогда 1º = 1,11…^д или 1^д = 0,9º. В некоторых случаях необходимо измерить массу или время. Тогда масса измеряется в килограммах, время – в секундах.

Прямые и косвенные методы измерений. Измерение – это процесс сравнения измеряемой величины и некоторой заранее определённой. Измерения бывают прямыми – когда измеряется непосредственно величина, и косвенные – когда измеряются некоторые величины, от которых искомая зависит функционально. Так, при измерении расстояния рулеткой используют прямой метод, при измерении площади – косвенный.

3.2 Классификация погрешностей и методы ослабления их влияния на результаты измерений. Под воздействием ряда факторов при измерениях возникают погрешности измерений – разности между результатом измерения и истинным значением. Измерения всегда сопровождаются погрешностями. Погрешности подразделяются на грубые – превышающие некоторый заранее определённый предел (как правило, это просчёты); систематические - входящие в результаты измерений по определённой математической зависимости (постоянные, периодические, односторонне действующие); случайные – величину и знак которых предсказать невозможно. Систематическую постоянную погрешность можно проиллюстрировать следующим примером. Пусть мы измеряем линейкой c номинальной длиной один метр некий отрезок, в котором она укладывается ровно три раза, тогда мы получаем длину отрезка равной 3 м. Предположим, что реальная длина линейки l = 1,001 м. Тогда действительная длина отрезка есть l×n = 3×1,001 = 3,003 м, а погрешность l_i = Δln = (1 – 1,001)×3 = 0,003. Если при измерении горизонтального угла α центр транспортира устанавливают не на вершину измеряемого угла A, а в точку A', то возникает погрешность, которую можно определить по формуле λ = AA' sin α. Это периодическая погрешность, изменяющаяся по периодическому закону.

Для ослабления влияния систематических погрешностей применяют: введение поправок (равных погрешности по модулю и противоположных по знаку); выбор методики измерений (погрешности входят в результаты измерений с противоположными знаками, что освобождает от их влияния среднее арифметическое); ограничивают условия измерений (минимизируют величину систематической погрешности). Случайной погрешностью называют такую погрешность, величину и знак которой до проведения эксперимента (измерения) невозможно предсказать. Случайные погрешности обладают рядом свойств (не превышают предельной погрешности, отклонения, равные по величине и противоположные по знаку – равновероятны, малые отклонения встречаются чаще больших), из которых вытекает, что среднее арифметическое случайных погрешностей стремится к нулю. Если имеется ряд результатов измерений одной и той же величины, то необходимо определить наиболее надёжное значение. За такое значение принимают арифметическую средину (среднее арифметическое). Среднее арифметическое является экспериментальной оценкой математического ожидания, поэтому среднее арифметическое называют вероятнейшим значением.

3.3 Точность измерений. Погрешности функций измеренных величин. Оценки точности измерений. Точность измерений выражает степень близости результата измерения к действительному значению. Из-за наличия случайных погрешностей эта близость различна для разных результатов. Если одну и ту же величину измеряют одним и тем же способом при одних и тех же условиях, то результаты таких измерений называются равноточными. Точность измерений выражает степень близости результата измерений к действительному значению величины. Точность измерений характеризуют средней величиной случайной погрешности (случайного отклонения от истинного значения). В качестве теоретической характеристики берут среднее квадратическое отклонение

σ = √(D(Δ)),

где D – дисперсия случайной погрешности измерения Δ. Так как величина σ – чисто теоретическая, то обычно пользуются средней квадратической погрешностью, или эмпирическим средним квадратическим отклонением, которое определяется по формуле

m = √(ΣΔ_i²/n) (формула Гаусса),

где Δ_i = l_i – Х – истинная погрешность i-того измерения. В случае, если не известно Х, используют отклонение результатов измерений l_i от вероятнейшего значения Х₀:

m = √(Σν_i²/(n – 1)) (формула Бесселя),

где ν_i = l_i – Х₀. При большом количестве измерений среднеквадратическая погрешность и квадратическое отклонение практически равны. Если известны средние квадратические погрешности некоторых величин, то можно определить среднеквадратическую погрешность функции от них. Если определена функция измеренных величин Φ = φ (x, y, …, z) и известны погрешности аргументов m_x, m_y, m_z, то квадрат средней квадратической погрешности функции вычисляют по формуле

m²_Φ = (∂φ/∂x)²m²_x +(∂φ/∂y)²m²_y + … + (∂φ/∂z)²m²_z,

где (∂φ/∂x), (∂φ/∂y), …, (∂φ/∂z) - частные производные от функции φ по аргументам x, y, …, z. Так, для линейной функции u = a₁x₁ + a₂x₂ +… + a_nx_n оценка точности имеет вид m_u² = Σ a_i²m_i².

Пусть имеется ряд измерений одной величины: l₁, l₂, …, l_n. Если средние квадратические погрешности этих измерений равны: m₁ = m₂ = … = m_n, то такой ряд называют равноточным. Таковыми будут, например, измерения, проведенные по одной методике одним и тем же прибором наблюдателями одинаковой квалификации. Если хотя бы одна из величин имеет среднюю квадратическую погрешность, отличную от других, то такой ряд называют неравноточным. Такое может произойти, если некоторые из ряда измерений производились прибором одной точности, а остальные – прибором другой точности. Для определения вероятнейшего значения и оценки точности используется понятие о весе. Вес результата измерения – это численная характеристика доверия к этому измерению. Вес p_i в общем виде характеризуют следующим отношением: p_i = c/m²_i, где с – постоянное для данного рада положительное число. Отметим, что от выбора численного значения величины «с» окончательный результат (вероятнейшее значение) и оценка его точности не зависят. Если даны результаты неравноточных измерений l₁, l₂, …, l_n и их веса p₁, p₂, …, p_n, то вероятнейшее значение вычисляют по формуле

Х₀ = Σp_il_i/Σp_i.

Для оценки точности вычисляют среднюю квадратическую погрешность измерения с весом p_i = 1. Эту погрешность называют погрешностью единицы веса и вычисляют по формуле

μ = √(Σp_iδ²_i /(n-1)),

где δ_i = l_i – Х₀ – отклонение от вероятнейшего значения (весового среднего). Для оценки точности Х и результатов измерений используют формулы

m_X0 = M = μ/√Σp_i, m_i = μ/√p_i.

Для назначения весов не обязательно знать средние квадратические погрешности измерений. Обычно используют косвенные характеристики.

Одной из важных задач теории погрешностей является вычисление допустимых невязок и расхождений при проведении геодезических работ. Отправной точкой для расчётов допусков служит то, что невязка является погрешностью самой невязки. Так как погрешность – разность между результатом измерения и его точным значением, то Δf = f – f_т = f, где Δf – погрешность невязки. Следовательно, предельно возможное значение невязки (допустимая невязка), совпадает с предельной погрешностью этой невязки (f_доп = Δf_пред). Предельную погрешность Δf_пред можно вычислить, если известна средняя квадратическая погрешность невязки m_f; тогда Δf_пред = τm_f, где τ может принимать значения 2, 2,5, 3 в зависимости от условий. Значение m_f может быть вычислено по известным правилам оценки точности функций в зависимости от вида геодезических операций.

Угловые измерения

3.4 Общие принципы измерения углов на местности. Для определения взаимного положения точек необходимо уметь измерять углы и расстояния. Для определения планового положения необходимо знать горизонтальные и вертикальные углы. Горизонтальным называют угол AOB между проекциями линий (направлений на точки) OA' и OB' на горизонтальную плоскость Q (рис. 9). Иначе: горизонтальный угол – это двугранный угол между отвесными плоскостями, проходящими через его стороны. Он отсчитывается по часовой стрелке. Вертикальным называют угол ν_a (ν_b) между линей OA' (OB') и горизонтальной плоскостью. Угол между направлением на зенит и направлением данной линии называется зенитным расстоянием. Он отсчитывается от горизонтальной плоскости к линии. Для измерения горизонтального угла над его вершиной на отвесной линии помещают центр градуированного круга – лимба, - установленного горизонтально. Тогда угол между направлениями на местности будет равен разности отсчетов между сечениями лимба (a и b) вертикальными плоскостями, проходящими через линии OA' и OB' на местности. Если круг оцифрован по часовой стрелке, то β = b – a.

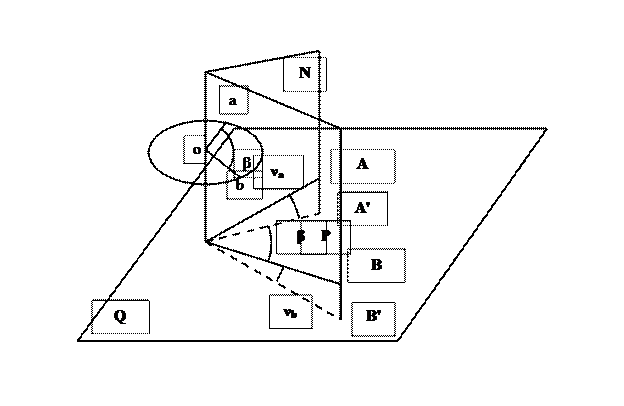
Рис. 9. Измерение горизонтальных и вертикальных углов.

3.5 Приборы для измерения углов. Описанный метод измерения углов реализован в теодолите. Основными частями теодолита являются горизонтальный и вертикальный круги, зрительная труба, цилиндрический уровень, подъёмные винты, винты закрепительные (алидад вертикального и горизонтального кругов и лимба горизонтального круга) и наводящие винты алидад вертикального и горизонтального кругов, а также лимба горизонтального круга. В принципиальной схеме теодолита выделяют четыре основных оси: вертикальную ось JJ', ось цилиндрического уровня UU', визирную ось VV' и ось вращения зрительной трубы TT' (рис. 10).

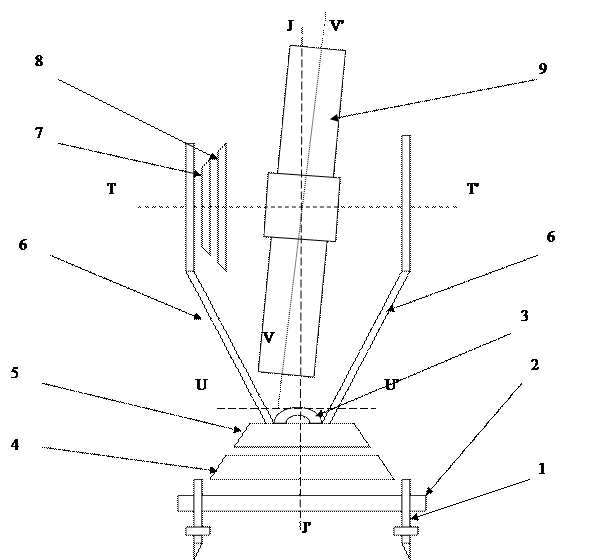
Рис. 10. Принципиальная схема теодолита.

На схеме условно обозначены: 1. подъёмные винты; 2. трегер; 3. цилиндрический уровень горизонтального круга; 4. лимб горизонтального круга; 5. алидада горизонтального круга; 6. колонка; 7. алидада вертикального круга; 8. лимб вертикального круга; 9. зрительная труба.

Рис. 11. Оптический теодолит 4Т15П. Увеличение зрительной трубы 20˟, средняя квадратическая погрешность измерения одним приёмом: вертикального угла – 15˝, горизонтального угла – 15˝.

3.6 Поверки и юстировки оптических теодолитов. Основные геометрические условия, которые должны быть соблюдены в теодолите, вытекают из принципиальной схемы измерения горизонтального угла и заключаются в следующем: 1. вертикальная ось (ось вращения алидады) инструмента должна быть отвесна, 2. плоскость лимба должна быть горизонтальна, 3. визирная плоскость должна быть вертикальна.

Для выполнения этих условий выполняются следующие поверки теодолита.

1. Ось цилиндрического уровня UU΄ при алидаде горизонтального круга должна быть перпендикулярна к вертикальной оси JJ΄ прибора.

2. Визирная ось зрительной трубы VV΄ должна быть перпендикулярна к горизонтальной оси TT΄ теодолита.

3. Горизонтальная ось вращения трубы TT΄ должна быть перпендикулярна к вертикальной оси JJ΄ прибора.

4. Одна из нитей сетки должна быть параллельна, другая перпендикулярна к вертикальной оси теодолита.

Первая поверка выполняется следующим образом. Пусть ось уровня не перпендикулярна вертикальной оси прибора и составляет с ним угол α. Тогда при повороте алидады на 180˚ угол также составит α, но при этом ось будет наклонена в другую сторону. Разность отсчётов по уровню даст величину 2α. Т.о., ось уровня необходимо наклонить на половину угла, равного разности отсчётов. На практике поверку выполняют так: пузырёк уровня, установленного параллельно двум подъёмным винтам, приводят в нуль-пункт. Сняв отсчёт по горизонтальному кругу, поворачивают алидаду на 180˚. При отклонении пузырька от середины ампулы выполняется юстировка: исправительными винтами его перемещают на половину отклонения; на вторую половину – подъёмными винтами. После этого поверку повторяют[1].

Угол отклонения визирной оси зрительной трубы от перпендикуляра к горизонтальной оси прибора называют коллимационной погрешностью. Для её определения наводят теодолит на удалённую точку и снимают отсчёт А при, скажем, круге право (КП). Переводят трубу через зенит и снова визируют эту точку при круге лево (КЛ), получая отсчёт В. Тогда при отсутствии погрешности В – А = ± 180˚. Если погрешность есть, то отсчёт при круге право будет отличаться от истинного отсчёта R на некоторую величину с: R=А+с. Очевидно, что для круга лево R=В – с ± 180˚, т.к. визирная ось отклонится в противоположную сторону. Т.о., среднее из отсчётов свободно от влияния коллимационной погрешности, а сама погрешность может быть найдена по формуле с = (В – А ± 180˚)/2. Для исключения коллимационной погрешности (в случае, если она превышает удвоенную точность отсчётного устройства) устанавливают на лимбе средний отсчёт; тогда центр сетки нитей сойдёт с визируемой точки. Исправительными винтами сетки совмещают её центр с визируемой точкой. Поверку повторяют.

Для проверки выполнения третьего условия теодолит устанавливают на расстоянии около 4-6 метров от какой-либо стены и, наведя перекрестие сетки нитей на точку М, при закрепленной алидаде опускают зрительную трубу до горизонтального положения визирной оси и отмечают на стене проекцию перекрестия сетки нитей. Переведя трубу через зенит, снова аналогичным способом проецируют ту же точку М. При совпадении точек условие выполнено. При несоблюдении данного условия устранение погрешности, вызванное неравенством колонок, возможно только в мастерской[2], так как в современных приборах отсутствуют исправительные винты подставок приборов.

Последнюю поверку выполняют одним из следующих способов. Центр сетки наводят на какую-либо точку и поворачивают трубу наводящим винтом алидады. Если при этом точка не сходит с горизонтальной нити, то условие выполнено. Иначе: на небольшом от прибора расстоянии (в безветренную погоду) подвешивают отвес и наводят на него вертикальную нить, которая должна совпадать с линией отвеса. В случае, если условие не выполнено, то, открепив юстировочные винты сетки нитей, следует повернуть её на необходимый угол. После закрепления винтов сетки нитей необходимо повторить вторую поверку.