Силы, действующие в зацеплении.
| Силы | Прямозубая передача | Косозубая передача |
| Окружная сила | 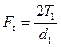
| 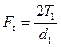
|
| Радиальная сила | 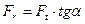 ( ( 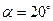 ) )
| 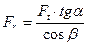
|
| Осевая сила | 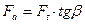
|
3.5.7. Конические зубчатые колеса применяют в передачах, оси валов которых пересекаются под некоторым межосевым углом 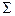 . Обычно
. Обычно 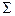 = 90° (рис. 3.5.7).
= 90° (рис. 3.5.7).
В сравнении с цилиндрическими конические передачи имеют большую массу и габариты, сложнее в изготовлении и монтаже. Одно из конических колес, как правило шестерня, располагается консольно, при этом вследствие повышенной деформации консольного вала увеличиваются неравномерность распределения нагрузки по ширине зубчатого венца и шум. Осевые силы, возникающие в передаче, вызывают необходимость применения сложных опор.
Не смотря на указанные недостатки, конические колёса применяют во всех отраслях машиностроения, где по условиям компоновки машины необходимо передать движение между пересекающимися осями валов.
Конические колеса бывают с прямыми и круговыми зубьями. Ось кругового зуба — это дуга окружности соответствующего диаметра резцовой головки. Угол наклона кругового зуба переменный. За расчетный принимают угол на окружности среднего диаметра колеса, обычно 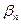 = 35°. Значение
= 35°. Значение 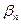 выбирают исходя из обеспечения плавности зацепления. Конические передачи с круговыми зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше.
выбирают исходя из обеспечения плавности зацепления. Конические передачи с круговыми зубьями по сравнению с прямозубыми имеют большую нагрузочную способность, работают более плавно и, следовательно, динамические нагрузки и шум при их работе меньше.
Для конических передач установлено 12 степеней точности и соответственно нормы точности. Предельные окружные скорости для конических прямозубых (непрямозубых) колёс: при 6-й степени – до 12 (20) м/с , 7-й степени – до 8 (10) м/с, 8-й степени – до 4 (7) м/с, 9-й – до 1,5 (3) м/с.
В конических колесах вводят понятие «начальные конусы» — это две конические поверхности с общей вершиной и образующей, перекатывающиеся одна по другой без скольжения. При этом начальные и делительные конусы всегда совпадают. Углы делительных конусов обозначают 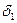 и
и 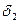 . Обязательным условием пердачи должно быть пересечение осей валов и образующих начальных конусов в одной точке.
. Обязательным условием пердачи должно быть пересечение осей валов и образующих начальных конусов в одной точке.
Передаточное число при межосевом угле 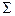 = 90°
= 90°
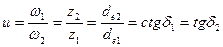
Для конической прямозубой передачи рекомендуется 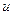 = 2; 2,5; 3,15; 4, для передачи скруговыми зубьями возможны более высокие значения
= 2; 2,5; 3,15; 4, для передачи скруговыми зубьями возможны более высокие значения 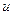 ; наибольшее значение
; наибольшее значение 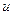 = 6,3.
= 6,3.
Профилирование эвольвентных зубьев конических колес выполняют приближённым способом Тредгольда - на поверхностях внешних дополнительных конусов с вершинами 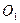 и
и 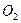 , образующие которых перпендикулярны образующим делительных конусов. Поверхности дополнительных конусов легко развертываются на плоскость: образующие внешних дополнительных конусов
, образующие которых перпендикулярны образующим делительных конусов. Поверхности дополнительных конусов легко развертываются на плоскость: образующие внешних дополнительных конусов 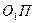 и
и 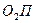 принимают за радиусы окружностей вершин эквивалентных цилиндрических колёс, образующие средних дополнительных конусов принимают за радиусы делительных окружностей эквивалентных цилиндрических колес. Профили зубьев эквивалентных цилиндрических колёс используют в качестве профилей зубьев конических колес.
принимают за радиусы окружностей вершин эквивалентных цилиндрических колёс, образующие средних дополнительных конусов принимают за радиусы делительных окружностей эквивалентных цилиндрических колес. Профили зубьев эквивалентных цилиндрических колёс используют в качестве профилей зубьев конических колес.
Внешние и внутренние дополнительные конусы определяют ширину зубчатого венца 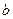 .
.
Высота зуба, шаг и модуль конического колеса переменны по длине зуба. Они максимальны на внешнем дополнительном конусе и минимальны на внутреннем. Для удобства измерения контроль размеров колеса при его изготовлении ведется по сечению зубьев поверхностью внешнего дополнительного конуса.
Высота зуба конического колеса переменна по длине зуба, а значит прочность зубьев конического колеса переменна по их длине. Поэтому прочность колес оценивается размерами по сечению зубьев шестерни поверхностью среднего дополнительного конуса, предполагая, что там лежит точка приложения нормальной силы 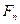 (рис. 3.5.8), т.е. силы, действующей перпендикулярно к поверхности зуба по делительному конусу. Силу
(рис. 3.5.8), т.е. силы, действующей перпендикулярно к поверхности зуба по делительному конусу. Силу 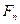 раскладывают на три составляющие:
раскладывают на три составляющие: 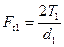 (окружная сила);
(окружная сила); 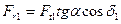 (радиальная сила);
(радиальная сила); 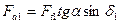 (осевая сила).
(осевая сила).
Для колеса направление сил противоположно, при этом:
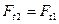 ,
, 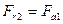 ,
, 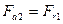 .
.
Направление окружных сил 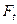 зависит от направления вращения колёс. Осевые силы
зависит от направления вращения колёс. Осевые силы 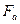 всегда направлены от вершин конусов, радиальные
всегда направлены от вершин конусов, радиальные 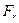 - к осям вращения колёс.
- к осям вращения колёс.
3.5.8. Расчёт прямозубых конических передач на прочность выполняют по формулам прямозубой цилиндрической передачей, но для расчётов конические колёса заменяют эквивалентными цилиндрическими прямозубыми колёсами. Диаметры и число зубьев эквивалентных колес:
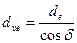 ,
, 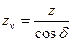 ,
,
где 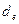 - внешний делительный диаметр,
- внешний делительный диаметр, 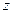 - действительное число зубьев конического колеса.
- действительное число зубьев конического колеса.
Модуль зубьев эквивалентного цилиндрического колеса принимается равным модулю 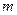 в среднем сечении зуба, а передаточное число эквивалентных колёс
в среднем сечении зуба, а передаточное число эквивалентных колёс 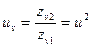 .
.
Кроме того, по опытным данным, нагрузочная способность конической передачи составляет 0,85 по сравнению с эквивалентной цилиндрической. Поэтому в знаменатель расчётных формул вводят 0,85 – коэффициент понижения допускаемой нагрузки для конических прямозубых передач.
С учётом сказанного, формула для проверочного расчёта зубьев для стального конического прямозубого колеса на контактную усталость:
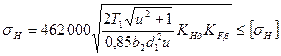 .
.
Тогда формула для проектного расчёта стального конического прямозубого колеса на контактнуюусталость:
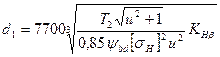 ,
,
или, так как основным размером, определяющим габариты конической передачи, является внешний диаметр колеса,
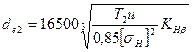 .
.
Формула для проверочного расчёта стального конического прямозубого колеса на усталость при изгибе:
.
Формула для проектного расчёта стального конического прямозубого колеса на усталость при изгибе:
.
По найденной величине среднего делительного окружного модуля определяется производственный модуль 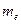 (внешний делительный окружной модуль).
(внешний делительный окружной модуль).
Далее определяют остальные размеры колёс (рис. 3.5.9).
| Геометрические параметры передачи | Прямозубая передача |
| Средний делительный окружной модуль | 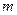
|
| Внешний делительный окружной модуль | 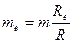
|
| Внешний делительный диаметр | 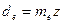
|
| Средний делительный диаметр | 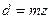
|
| Внешнее конусное расстояние | 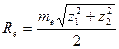
|
| Ширина зубчатого венца колеса | 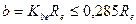
|
| Коэффициент ширины зубчатого венца относительно внешнего конусного расстояния | 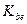
|
| Среднее конусное расстояние | 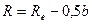
|
| Внешняя высота головки зуба | 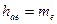
|
| Внешняя высота ножки зуба | 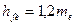
|
| Высота зуба | 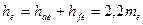
|
| Диаметр вершин зубьев | 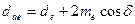
|
3.5.9. Эвольвентное зацепление, созданное в России в 1754 г. академиком Леонардо Эйлером, получило в технике самое широкое распространение благодаря своим достоинствам, но оно имеет и свои недостатки: ограниченная нагрузочная способность передач; повышенная чувствительность колес к перекосам из-за линейных контактов зубьев; существенные потери на трение в зацеплении.
Ограниченная нагрузочная способность объясняется тем, что контакт зубьев происходит по линии (практически по узкой площадке), расположенной вдоль зуба. Вследствие малого приведенного радиуса кривизны рабочих поверхностей зубьев возникают значительные контактные напряжения, ограничивающие контактную прочность зубьев.
Кроме того, возникают трудности при обеспечении необходимого линейчатого контакта сопряжённых зубьев, что вынуждает конструкторов прибегать к повышенной жёсткости валов, зубьев и корпусов, так как упругие деформации в конструкции передачи влекут за собой нарушение правильности зацепления.
Для повышения контактной прочности, а следовательно, несущей способности зубчатых передач в 1954 г. М. Л. Новиковым было разработано новое зубчатое зацепление (3.5.10), в котором первоначальный линейный контакт (линейное эвольвентное зацепление) заменен точечным зацеплением, в котором профили зубьев колес в торцовом сечении очерчены дугами окружности весьма близких радиусов. Зуб шестерни делается выпуклым, а зуб колеса — вогнутым, что увеличивает их приведенный радиус кривизны, зубья соприкасаются на значительной длине — площадке контакта, тем самым повышая контактную прочность передачи примерно в 3-4 раза по сравнению с эвольвентными передачами тех же размеров.
В зацеплении Новикова вместо линии зацепления имеется точка зацепления. Зубья касаются только в момент прохождения профилей через эту точку, а непрерывность передачи движения обеспечивается винтовой формой зубьев. Поэтому зацепление Новикова может быть только косозубым. Практически угол наклона зубьев 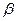 = 10...22°.
= 10...22°.
Теоретически доказано, что самой выгодной формой профиля зуба будет окружность с центром на линии центров.
Недостаткипередач Новикова:
· повышенная чувствительность к изменению межосевого расстояния;
· невозможность осуществления конструкции колёс с прямым зубом;
· ширина колёс должна быть не менее шести модулей зацепления;
· технологические трудности при производстве колёс.
Зацепление Новикова применяется для всех видов зубчатых передач как с наружным, так и внутренним зацеплением.
Передачи с круговым зацеплением Новикова наиболее пригодны в тех случаях, когда нагрузочная способность передачи определяется контактной прочностью при твердости рабочих поверхностей менее 350 НВ, при относительно постоянных режимах и скоростях до 12 м/с. В этом случае их нагрузочная способность примерно в 2 раза больше, чем эвольвентных прямозубых передач.
Передачи с зацеплением Новикова стандартизованы. Расчет их ведут аналогично расчету передач с эвольвентным зацеплением с учетом их особенностей. Результаты расчета показали, что габариты передач Новикова по сравнению с эвольвентными на 20...25% меньше при одинаковом нагружении, т. е. они более компактны и допускают большие передаточные числа.
2.5.10. Планетарными называют передачи, имеющие зубчатые колеса с перемещающимися осями. Эти колеса называют сателлитами. Зубчатые колеса, с которыми сцепляются сателлиты, называют центральными. Геометрические оси этих колес совпадают с осью вращения ведущего и ведомого валов передачи, которую называют центральной осью.
Планетарная передача на рисунке 3.5.11 состоит из подвижного центрального колеса с наружными зубьями, сателлитов, неподвижного центрального колеса с внутренними зубьями и водила, на котором укреплены оси сателлитов.
Сателлиты совершают сложное движение — вращаются вокруг своих осей, закрепленных на водиле, и одновременно вместе с водилом вращаются вокруг центрального колеса, т. е. совершают движение, подобное движению планет солнечной системы, отчего планетарные передачи и получили свое название.
При неподвижном центральном колесе движение может передаваться от центрального колеса к водилу или от водила к колесу, т. е. ведущим звеном в планетарной передаче может быть либо центральное колесо, либо водило. Это позволяет при одной и той же схеме передачи получать различные передаточные числа. В случае неподвижного водила движение может передаваться от колеса с внутренними зубьями к колесу с внешними зубьями или наоборот.
Планетарную передачу, в которой одно из центральных колес неподвижно, называют простейшей.В отличие от простейшей планетарную передачу, в которой все зубчатые колеса и водило подвижны (свободны), называют дифференциальной.В дифференциальной передаче одно движение можно раскладывать на два или два движения соединить в одно. Например, движение колеса с внутренними зубьямираскладывается на два движения: движение колеса с внешними зубьями и движение водила.
Достоинства: большое передаточное число в одной ступени, а также малые габариты и масса. Снижение массы (обычно в 2...4 раза и более) объясняется следующими причинами: распределением нагрузки между сателлитами, благодаря чему нагрузка на зубья в каждом зацеплении уменьшается в несколько раз; широким применением зубчатых колес с внутренним зацеплением, обладающих повышенной нагрузочной способностью; малой нагрузкой на опоры. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются. Планетарные передачи работают с меньшим шумом, что связано с повышенной плавностью внутреннего зацепления и меньшими размерами колес.
Недостатки: повышенные требования к точности изготовления и монтажа; резкое снижение КПД передачи с увеличением передаточного числа.
Планетарную передачу применяюткак редуктор с постоянным передаточным числом; как коробку скоростей, передаточное число в которой изменяется путем поочередного торможения различных звеньев (например, водила или одного из колес); как дифференциальный механизм. Их успешно применяют в транспортном машиностроении, станкостроении, приборостроении и т. д.
ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
3.6.1. Червячной передачей (ЧП) называется механизм, служащий для преобразования вращательного движения между валами со скрещивающимися осями. Обычно червячная передача (рис. 3.6.1) состоит из червяка1 и сопряженного с ним червячного колеса 2.Угол скрещивания осей обычно равен 90°; неортогональные передачи встречаются редко. Червячные передачи относятся к передачам зацеплением, в которых движение осуществляется по принципу винтовой пары. Зубья колеса имеют вогнутую форму, что увеличивается длину контактных линий, а следовательно, улучшает качество работы передачи.
Обычно ведущее звено червячной передачи — червяк, но существуют механизмы, в которых ведущим звеном является червячное колесо. Конструктивно червячные передачи чаще всего делают в закрытом исполнении.
Достоинства ЧП:
· возможность получения больших передаточных чисел в одноступенчатой передаче (до300 и более) при малых габаритах;
· высокая кинематическая точность и повышенная плавность работы;
· малая интенсивность шума и виброактивности;
· возможность обеспечения самоторможения (движение может передаваться только в одном направлении).
НедостаткиЧП:
· значительное геометрическое скольжение в зацеплении и связанные с этим трение, повышенный износ, склонность к заеданию, нагрев передачи и сравнительно низкий КПД (от 0,5 до 0,95;0,5 для самотормозящихся передач);
· необходимость применения для ответственных передач дорогостоящих и дефицитных антифрикционных цветных металлов;
· высокая стоимость инструмента для нарезания червячных колёс (червячные фрезы); для шлифовки червяков требуются специальные станки или сложные приспособления.
· ограниченная мощность червячных передач (обычно до 60 кВт); передача большой мощности невыгодна из-за больших потерь и сильного нагрева.
ЧП находят широкое применение, например, в металлорежущих станках, подъемно-транспортном оборудовании, транспортных машинах, а также в приборостроении. Червячные передачи во избежании их перегрева предпочтительно использовать в приводах периодического (а не непрерывного) действия.
КлассификацияЧП:
· по расположению червяка (рис. 3.6.2) относительно колеса: с нижним, верхним и боковым червяком (расположение червяка определяется компоновкой изделия);
· по форме поверхности, на которой нарезают витки: с глобоидными (рис. 3.6.3) и цилиндрическими (рис. 3.6.4) червяками (глобоидные передачи более надёжны и долговечны, имеют в 1,5 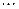 2 раза большую нагрузочную способность, но требуют повышенной точности изготовления и монтажа; применяются реже цилиндрических);
2 раза большую нагрузочную способность, но требуют повышенной точности изготовления и монтажа; применяются реже цилиндрических);
· по форме профиля витка цилиндрического червяка: с архимедовыми ZA, эвольвентными ZJ и конволютными ZN червяками.
При прочих равных условиях форма профиля витков червяка мало влияет на нагрузочную способность передачи, поэтому технология изготовления является решающим фактором при выборе профиля витков. Наибольшее распространение получили цилиндрические передачи с архимедовымчервяком.
Червяки, как правило изготавливают как одно целое с валом, что увеличивает жёсткость и снижает стоимость. В передачах с малыми передаточными числами и большими диаметрами червяков применяют насадные червяки. Как все винты, червяки могут быть одно- или многозаходными; иметь правое или левое направления резьбы. Стандарт предусматривает применение одно-, двух- и четырёхзаходных червяков, обычно с линией витков правого направления. Червяки с числом заходов выше четырёх применяются очень редко, так как технология их изготовления усложнена.
Для цилиндрических червячных передач установлено 12 степеней точности. Выбор степени точности производится в зависимости от скорости скольжения 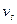 . Для силовых передач наибольшее применение находят 7-я (при
. Для силовых передач наибольшее применение находят 7-я (при 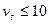 м/с), и 8-я (при
м/с), и 8-я (при 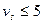 м/с) степени точности.
м/с) степени точности.
Передаточное число ЧП равно отношению числа зубьев червячного колеса к числу витков червяка:
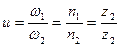 .
.
В силовых передачах передаточные числа принимают в пределах 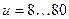 .
.
3.6.2. Коренным отличием червячной передачи от зубчатой состоит в том, что скорость скольжения в червячном зацеплении больше окружной скорости червяка.
Повышенное скольжение в зацеплении возникает потому, что окружные скорости 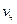 червяка и
червяка и 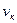 колеса направлены под углом скрещивания одна к другой (рис. 3.6.5). Поэтому ветки червяка скользят по зубьям колеса, причём
колеса направлены под углом скрещивания одна к другой (рис. 3.6.5). Поэтому ветки червяка скользят по зубьям колеса, причём
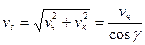 ,
,
где 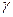 - угол подъёма линии витка червяка.
- угол подъёма линии витка червяка.
Повышенное скольжение в зацеплении является причиной пониженного КПД, повышенного изнашивания зубьев и склонности к заеданию.
Коэффициент полезного действия червячной передачи определяется потерями на трение в зацеплении, потерями на перемешивание и разбрызгивание масла и потерями в опорах валов. Общий КПД ЧП определяется по формуле
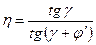 ,
,
где 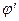 - приведённый угол трения, зависящий от скорости скольжения. Табличные значения
- приведённый угол трения, зависящий от скорости скольжения. Табличные значения 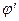 получены экспериментально с учётом потерь в подшипниках и на разбрызгивание и размешивание масла.
получены экспериментально с учётом потерь в подшипниках и на разбрызгивание и размешивание масла.
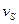 , м/с , м/с
| 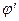
| 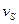 , м/с , м/с
| 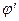
|
| 0,01 0,10 0,50 1,00 1,50 2,00 | 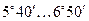
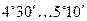
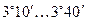
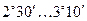
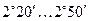
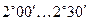
| 2,5 3,0 4,0 7,0 10,0 15,0 | 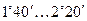
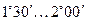
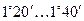
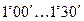
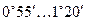
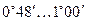
|
Из формулы следует, что КПД увеличивается с возрастанием числа витков червяка (увеличивается 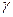 ) и с уменьшением коэффициента трения ( уменьшается
) и с уменьшением коэффициента трения ( уменьшается 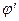 , т.к.
, т.к. 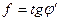 ).
).
При проектном расчёте, когда размеры передачи ещё не известны, значение КПД ориентировочно можно определить по формуле
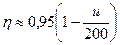 .
.
Таким образом, при выборе материалов червячной пары необходимо обеспечить хорошие антифрикционные и противозадирные свойства. Наилучшие результаты достигаются при сочетании высокотвёрдой стальной поверхности с антифрикционным материалом, например бронзой.
При работе червяки испытывают большие напряжения изгиба и кручения, а также напряжения растяжения (сжатия). Вследствие этого, а также из-за высоких требований к жёсткости червяки изготавливают из сталей, закалённых до высокой твёрдости. При этом необходима шлифовка и полировка рабочих поверхностей витков червяка. Высокая твёрдость и гладкость витков обеспечивают наибольшую стойкость зубьев червячных колёс против изнашивания и усталостного разрушения.
В целях экономии цветных металлов червячные колёса чаще всего делают составными: на чугунный или стальной центр насаживают бронзовый венец. Марку бронзы выбирают в зависимости от скорости скольжения, ожидаемое значение которой ориентировочно определяют по формуле
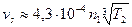 .
.
3.6.3. Наиболее характерные виды разрушения: заедание и изнашивание зубьев червячного колеса, как менее прочного элемента передачи. Так как заедание и изнашивание зубьев зависят от контактных напряжений, то основными критериями работоспособности и расчёта червячных передач являются контактная прочность рабочих поверхностей зубьев колеса. При этом расчёт на изгиб производится как проверочный.
В червячных передачах из-за повышенного трения скольжения в зацеплении происходит выделение большого количества теплоты, которая нагревает масло, а оно через стенки корпуса передает эту теплоту окружающей среде. Если отвод теплоты недостаточен, передача перегревается. При перегреве смазочные свойства масла резко ухудшаются (уменьшается вязкость), увеличиваются изнашивание червячного колеса и опасность заедания, что может привести к выходу передачи из строя. Тепловой расчёт для червячных передач проводится как проверочный.
Кроме того, для обеспечения правильности зацепления червяка с червячным колесом червяк должен быть достаточно жёстким. Наибольший прогиб червяка не должен превышать 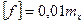 . При проверочном расчёте тело червяка рассматривают как цилиндрический брус круглого сечения, лежащий в двух опорах и работающий на изгиб и кручение.
. При проверочном расчёте тело червяка рассматривают как цилиндрический брус круглого сечения, лежащий в двух опорах и работающий на изгиб и кручение.
3.6.4. Расчёт на контактную усталость зубьев червячного колеса. Этот расчёт должен обеспечивать не только отсутствие усталостного разрушения поверхностей зубьев, но и отсутствие заедания.
В основу расчёта положены формула Герца для определения наибольшего контактного напряжения 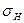 и нормальная нагрузка на единицу длины контактных линий.
и нормальная нагрузка на единицу длины контактных линий.
Упрощённая формула для проверочного расчётаЧП на контактную усталость имеет вид:
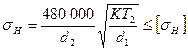 ,
,
где 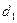 - делительный диаметр червяка;
- делительный диаметр червяка;
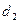 - делительный диаметр червячного колеса;
- делительный диаметр червячного колеса;
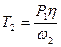 - вращающий момент на валу червячного колеса;
- вращающий момент на валу червячного колеса;
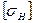 - допускаемое контактное напряжение;
- допускаемое контактное напряжение;
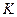 - коэффициент нагрузки: при постоянной нагрузке
- коэффициент нагрузки: при постоянной нагрузке 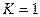 , при переменной нагрузке
, при переменной нагрузке 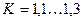 (большие значения для высокоскоростных передач).
(большие значения для высокоскоростных передач).
Коэффициент нагрузки при расчёте червячных передач невелик, так как они работают плавно, бесшумно и хорошо прирабатываются.
При проектном расчёте основным расчётным параметром является межосевое расстояние 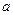 . Приравняв контактное напряжение
. Приравняв контактное напряжение 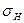 допускаемому
допускаемому 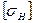 , получим формулу для проектного расчёта цилиндрических червячных передач:
, получим формулу для проектного расчёта цилиндрических червячных передач:
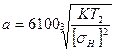 .
.
Для червячных колёс из оловянных бронз и стальных червяков значения допускаемого контактного напряжения 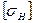 при заданном числе циклов
при заданном числе циклов 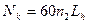 (
( 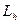 - заданная долговечность), отличном от базы испытаний, определяется по формуле
- заданная долговечность), отличном от базы испытаний, определяется по формуле
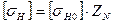 ,
,
где 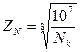 - коэффициент долговечности;
- коэффициент долговечности; 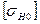 -значения допускаемых контактных напряжений при базе испытаний
-значения допускаемых контактных напряжений при базе испытаний 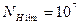 циклов нагружения.
циклов нагружения.
| Материал и способ отливки | 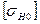 при твёрдости поверхности витков червяка при твёрдости поверхности витков червяка 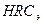 , МПа , МПа
| |
| <45 | 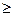 45 45
| |
| БрО10Ф1, в песок БрО10Ф1, в кокиль БрО10Н1Ф1, центробежная |
Значения допускаемых контактных напряжений 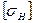 для червячных колёс из чугуна или безоловянной бронзу и стальных червяков выбирают независимо от циклов нагружений по таблице.
для червячных колёс из чугуна или безоловянной бронзу и стальных червяков выбирают независимо от циклов нагружений по таблице.
| Материал | 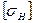 при скорости скольжения при скорости скольжения 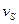 (м/с), МПа (м/с), МПа
| |||||||
| червяка | Червячного колеса | 0,25 | 0,5 | |||||
Сталь 20; 20Х,
цементуемая
( Н> 45 НRС 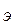 )
Сталь 45, Ст6
Сталь закалённая )
Сталь 45, Ст6
Сталь закалённая
| СЧ15, СЧ18 СЧ15, СЧ18 БрА9Ж4Л |
По величине межосевого расстояния определяют расчётный модуль 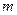 по формуле
по формуле
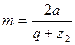 ,
,
округляя его до ближайшего стандартного значения, а затем уточняют значение межосевого расстояния
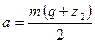 .
.
После установления основных параметров передачи определяют размеры червяка и колеса, вычисляют скорость скольжения 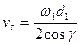 , находят расчётное значение КПД
, находят расчётное значение КПД 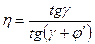 и вращающего момента
и вращающего момента 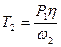 на валу червячного колеса, а затем проводят проверочный расчёт , сравнивая расчётное контактное напряжение с допускаемым, причём недогрузка желательна не более 10%, а перегрузка не должна превышать 5%.
на валу червячного колеса, а затем проводят проверочный расчёт , сравнивая расчётное контактное напряжение с допускаемым, причём недогрузка желательна не более 10%, а перегрузка не должна превышать 5%.
Геометрические параметры червяка(рис. 3.6.6)и червячного колеса(рис 3.6.7).
| Геометрические параметры передачи | Червяк |
| Угол профиля витка в осевом сечении | 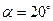
|
Число винтовых червяка
при 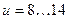 при
при 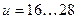 при
при 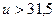 или для самотормозящей передачи или для самотормозящей передачи
|
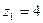
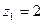
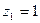
|
| Коэффициент диаметра червяка | 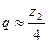
|
| Делительный диаметр | 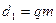
|
| Высота головки витка червяка | 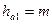
|
| Высота ножки витка червяка | 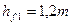
|
| Высота витка червяка | 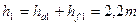
|
| Диаметр вершин витков | 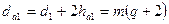
|
| Диаметр впадин витков | 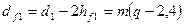
|
Длина нарезанной части червяка
при 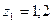 при
при 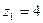
|
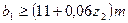
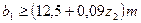
|
| Делительный угол подъёма линии витка | 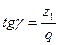
|
| Расчётный шаг червяка | 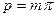
|
| Ход червяка | 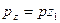
|
Примечание. 1) С увеличением 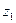 повышается КПД передачи, но усложняется технология её изготовления и увеличивается число зубьев червячного колеса
повышается КПД передачи, но усложняется технология её изготовления и увеличивается число зубьев червячного колеса 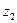 , а следовательно, при данном передаточном числе увеличиваются габариты передачи.
, а следовательно, при данном передаточном числе увеличиваются габариты передачи.
2) Шаг червяка должен быть равен шагу колеса.
3) Чтобы исключить слишком тонкие червяки, стандарт предусматривает увеличение 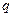 с увеличением
с увеличением 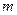 . Вообще большие значения
. Вообще большие значения 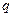 рекомендуется принимать при больших передаточных числах (увеличенных расстояниях между опорами червяка), чтобы обеспечит достаточную изгибную жёсткость червяка.
рекомендуется принимать при больших передаточных числах (увеличенных расстояниях между опорами червяка), чтобы обеспечит достаточную изгибную жёсткость червяка.
Стандартные значения 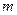 (для червячных передач), мм.
(для червячных передач), мм.
| 1-й ряд | 1,0 | 1,25 | 1,6 | 2,0 | 2,5 | 3,15 | 4,0 | 5,0 | 6,3 | 8,0 | |
| 2-й ряд | 1,5 | 3,0 | 3,5 | 6,0 | 7,0 |
Стандартные значения коэффициента диаметра червяка 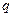 .
.
| 1-й ряд | 8,0 | 10,0 | 12,5 | 16,0 | 20,0 | 25,0 |
| 2-й ряд | 7,1 | 9,0 | 11,2 | 14,0 | 18,0 | 22,4 |
| Геометрические параметры передачи | Червячное колесо |
| Делительный диаметр | 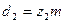
|
| Число зубьев червячного колеса | 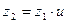 ( рекомендовано
( рекомендовано 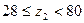 ) )
|
| Высота головки зуба | 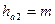
|
| Высота ножки зуба | 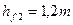
|
| Высота витка червяка | 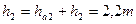
|
| Диаметр вершин зубьев | 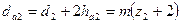
|
| Диаметр впадин зубьев | 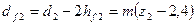
|
| Наибольший диаметр червячного колеса | 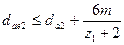
|
Ширина венца колеса
при 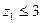 при
при 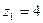
|
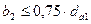
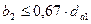
|
Примечание. 1) Минимальное число зубьев колеса 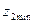 определяют из условия отсутствия подрезания и обеспечения достаточной поверхности зацепления. Для силовых передач
определяют из условия отсутствия подрезания и обеспечения достаточной поверхности зацепления. Для силовых передач 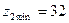 .
.
2) При увеличении 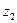 возрастают диаметр колеса и расстояние между опорами червяка, что приводит к увеличению его деформирования. При
возрастают диаметр колеса и расстояние между опорами червяка, что приводит к увеличению его деформирования. При 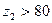 возникает опасность излома зубьев ввиду уменьшения модуля.
возникает опасность излома зубьев ввиду уменьшения модуля.
Расчёт зубьев червячного колеса на усталость при изгибе. Указанный расчёт является проверочным и аналогичен расчёту зубьев цилиндрических косозубых колёс; за счёт дугообразной формы зубья червячного колеса полагаются приблизительно на 40% прочнее.
Формула для проверочного расчётазубьев червячного колеса на усталость при изгибе имеет вид
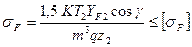 ,
,
где 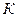 - коэффициент нагрузки: при постоянной нагрузке
- коэффициент нагрузки: при постоянной нагрузке 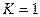 , при переменной нагрузке
, при переменной нагрузке 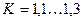 ;
;
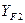 - коэффициент формы зуба, принимаемый по эквивалентному числу зубьев
- коэффициент формы зуба, принимаемый по эквивалентному числу зубьев 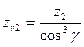 ;
;
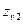
| |||||||||
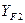
| 1,98 | 1,88 | 1,85 | 1,80 | 1,76 | 1,71 | 1,64 | 1,61 | 1,55 |
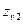
| |||||||||
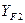
| 1,48 | 1,45 | 1,40 | 1,34 | 1,30 | 1,27 | 1,24 |
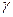 - угол подъёма линии витка червяка;
- угол подъёма линии витка червяка;
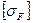 - допускаемые напряжения изгиба.
- допускаемые напряжения изгиба.
Допускаемые напряжения изгиба 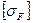 для зубьев червячного колеса устанавливаются в зависимости от материала, способа отливки и характера нагружения (реверсивное, нереверсивное).
для зубьев червячного колеса устанавливаются в зависимости от материала, способа отливки и характера нагружения (реверсивное, нереверсивное).
Значения допускаемого напряжения изгиба при расчётном числе циклов 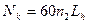 (
( 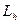 - заданная долговечность) определяют по формуле
- заданная долговечность) определяют по формуле
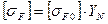 ,
,
где 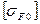 - допускаемые напряжения изгиба при базе испытаний
- допускаемые напряжения изгиба при базе испытаний 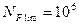 циклов нагружений;
циклов нагружений;
| Материал и способ отливки | 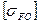 , МПа , МПа
| |
| Нереверсивное нагружение | Реверсивное нагружение | |
| БрО10Ф1, в песок БрО10Ф1, в кокиль БрО10Н1Ф1, центробежный БрА9Ж4Л, в песок СЧ10 » СЧ15 » СЧ18 » |
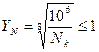 - коэффициент долговечности; если
- коэффициент долговечности; если 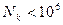 , то его принимают равным базе испытаний
, то его принимают равным базе испытаний 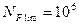 ; если
; если 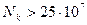 , то принимают
, то принимают 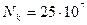 .
.
Силы, действующие в зацеплении(рис. 3.6.8).
| Силы | Червяк | Червячное колесо |
| Окружная сила | 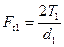
| 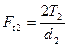
|
| Осевая сила | 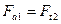
| 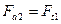
|
| Радиальная сила | 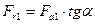 , , 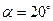
| 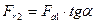
|
3.6.5. Тепловой расчет червячной передачи при установившемся режиме работы выполняют как проверочный на основе теплового баланса:
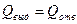 ,
,
где 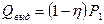 — количество теплоты, выделяемой работающей передачей в одну секунду;
— количество теплоты, выделяемой работающей передачей в одну секунду;
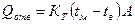 — количество теплоты, отводимой наружной поверхностью корпуса в 1 с.
— количество теплоты, отводимой наружной поверхностью корпуса в 1 с.
Из условия теплового баланса находим температуру масла в корпусе червячного редуктора, °С, при непрерывной работе:
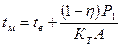 ,
,
где 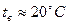 — температура окружающего воздуха;
— температура окружающего воздуха;
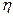 — КПД червячной передачи;
— КПД червячной передачи;
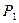 — мощность на валу червяка, Вт;
— мощность на валу червяка, Вт;
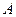 — поверхность охлаждения корпуса
— поверхность охлаждения корпуса
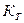 — коэффициент теплопередачи,
— коэффициент теплопередачи, 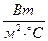 , т. е. число, показывающее, сколько теплоты в секунду передается одним квадратным метром поверхности корпуса при перепаде температур в один градус.
, т. е. число, показывающее, сколько теплоты в секунду передается одним квадратным метром поверхности корпуса при перепаде температур в один градус.
Коэффициент теплопередачи зависит от материала корпуса редуктора и скорости циркуляции воздуха. Для чугунных корпусов принимают 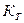 = 9... 17
= 9... 17 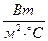 . Большие значения используют при хорошей циркуляции воздуха вокруг корпуса и интенсивном перемешивании масла (при нижнем или боковом расположении червяка).
. Большие значения используют при хорошей циркуляции воздуха вокруг корпуса и интенсивном перемешивании масла (при нижнем или боковом расположении червяка).
Поверхность 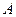 охлаждения корпуса (без учета поверхности дна), омываемая свободно циркулирующим воздухом, м2, определяют по размерам корпуса, полученным при эскизном проектировании. Ориентировочно
охлаждения корпуса (без учета поверхности дна), омываемая свободно циркулирующим воздухом, м2, определяют по размерам корпуса, полученным при эскизном проектировании. Ориентировочно 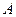 определяют по эмпирической формуле
определяют по эмпирической формуле
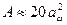 ,
,
где 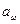 — межосевое расстояние, м.
— межосевое расстояние, м.
Условие работы передачи без перегрева
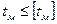 ,
,
где 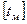 — максимально допускаемая температура нагрева масла. При нижнем расположении червяка
— максимально допускаемая температура нагрева масла. При нижнем расположении червяка 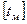 = 95°C, при верхнем —
= 95°C, при верхнем — 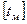 = 75° С. Если при расчете получили
= 75° С. Если при расчете получили 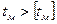 , то необходимо увеличить поверхность охлаждения
, то необходимо увеличить поверхность охлаждения 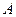 (рис. 3.6.9), применяя охлаждающие ребра (в расчете учитывается полная поверхность вертикальных ребер и только 50% поверхности горизонтальных), или применить искусственное охлаждение (3.6.10), которое осуществляется следующими способами:
(рис. 3.6.9), применяя охлаждающие ребра (в расчете учитывается полная поверхность вертикальных ребер и только 50% поверхности горизонтальных), или применить искусственное охлаждение (3.6.10), которое осуществляется следующими способами:
1) обдувают корпус воздухом с помощью вентилятора, насажанного на вал червяка; при этом 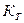 повышается до 20...28
повышается до 20...28 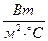 ;
;
2) охлаждают масло водой, проходящей через змеевик; в этом случае 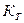 повышается до 90... 200
повышается до 90... 200 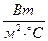 при скорости воды в трубе до 1 м/с;
при скорости воды в трубе до 1 м/с;
3) применяют циркуляционные системы смазки со специальными холодильниками.
В первых двух случаях, а также при естественном охлаждении смазка осуществляется путем погружения червяка или колеса в масло. Во избежание больших потерь на разбрызгивание и размешивание масла, а также для того, чтобы масло не вспенивалось (при этом снижаются смазочные свойства), глубина погружения колеса в масло не должна превышать высоты зуба, а глубина погружения червяка — не более высоты витка.
При последних двух способах интенсивность охлаждения зависит не только от площади поверхности охлаждения корпуса редуктора, поэтому применять вышеприведённые формулы для теплового расчёта нельзя.
Дата добавления: 2015-11-28; просмотров: 4231;
