Расчет атмосферных горелок

Расчет головной части горелки. Важным показателем работы атмосферной горелки является скорость выхода газовоздушной смеси из отверстий головной части W₀. Значения скорости выхода газовоздушной смеси W₀.принимается так, чтобы W₀.> W_пр; W₀.< W_отр, где W_отр, W_пр - предельные скорости отрыва и проскока, их значения для некоторых газов в зависимости от значений 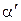, d₀ приведены, соответственно, в таблицах 1 и 2

Таблица 1

Предельные скорости проскока W_пр, отнесенные

к нормальным условиям, м/с

Диаметр отверстия, мм	Газ
коксовый	природный	бутан
коэффициент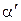
0,7	0,8	0,7	0,8	0,7	0,8
	0,75	1,0	0,1	0,25	0,2	0,4
	1,0	1,6	0,1	0,25	0,2	0,4

Таблица 2

Предельные скорости отрыва W_отр, отнесенные

к нормальным условиям, м/с

Диаметр отверстия, мм	Газ
коксовый	природный	бутан
коэффициент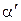
0,7	0,8	0,5	0,6	0,7	0,8	0,6	0,7	0,8
	8,3	6,9	1,7	1,3	1,0	0,8	1,15	0,9	0,7
	8,75	7,25	1,9	1,5	1,2	0,95	1,2	0,95	0,75
	9,75	8,2	2,55	2,15	1,75	1,3	1,55	1,3	1,1
	11,15	9,5	3,4	2,95	2,5	2,1	1,85	1,65	1,35
	-	-	4,5	4,0	3,5	3,0	-	-	-

Необходимая суммарная площадь выходных отверстий F₀ определяется из выражения

,

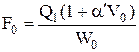где Q₁ - производительность горелки; W₀ - скорость выхода газовоздушной смеси из отверстий горелки, отнесенная к нормальным условиям (температура 0°С и давление 101,3 кПа); V₀ - объем теоретически необходимого воздуха для горения газа, м³/м³.

Расчет эжекционного смесителя горелки. Эжекционный смеситель состоит из следующих основных элементов (см. рис.1):

Рис. 1 Схема эжекционной атмосферной горелки:

1 - сопло; 2 - конфузор; 3 - горловина; 4 - диффузор; 5 - кратер; 6 - насадок (головная часть); 7 - отверстия для выхода газовоздушной смеси

сопла 1, из которого выходит газ; камеры смешения, состоящей из конфузора 2 и горловины 3 (цилиндрической части), в которых осуществляется смешение газа с воздухом, поступающим из атмосферы; диффузора 4, в котором завершается процесс смесеобразования и обеспечивается повышение давления газовоздушной смеси для преодоления гидравлического сопротивления выходных отверстий в головной части горелки.

Основное уравнение для расчета эжектора имеет следующий вид [1]:

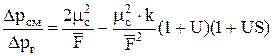, (1)

где Δр_см - давление газа, создаваемое эжектором; Δр_г - располагаемое (избыточное) давление газа перед соплом; μ_с - коэффициент расхода сопла; - основной параметр эжектора (F_г, F_с - соответственно, площадь горловины и сопла в безразмерном виде); k - коэффициент потерь эжекционного смесителя:

,

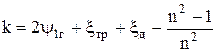где ψ_1г - коэффициент неравномерности скоростного поля по количеству движения; ξ_тр, ξ_д - коэффициенты сопротивления трению и диффузора, соответственно; n = F_д/F_г - степень расширения диффузора); U = М₁/М₂ - массовый коэффициент эжекции, представляющий отношение массового расхода газа к массовому расходу воздуха; S = ρ_г/ρ_в - относительная плотность газа (ρ_г, ρ_в - плотности газа и воздуха, соответственно).

Уравнение (1) связывает безразмерное давление, создаваемое эжектором Δр_см/Δр_г, с коэффициентом эжекции U и основным параметром .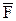

Основное уравнение атмосферной горелки имеет вид:

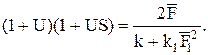(2)

Из уравнения (2) видно, что эжекционная способность горелки зависит только от конструкции горелки и не зависит от режима ее работы. Следовательно, горелка обладает саморегулируемостью. Это положение подтверждается экспериментально. Однако при значительных отклонениях режима работы горелки от оптимального саморегулируемость горелки нарушается [1].

Оптимальное значение параметра горелки определяется из выражения:

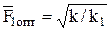, (3)

где k - коэффициент потерь эжекционного смесителя, принимается в зависимости от конструкции эжектора (рис. 10.3); k₁ - коэффициент, учитывающий потери энергии в головной части горелки:

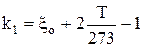, (4)

где - коэффициент сопротивления отверстий; Т - температура подогрева в выходных каналах, принимается в пределах 50-150°С.

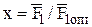Рис. 2. Конструкции эжекционных смесителей атмосферной горелки:

а - с оптимальной формой проточной части (k = 1,0); б, в - с укороченной формой проточной части, соответственно k = 2,1 и 3,0

В результате преобразований получаем:

Ах² - 2х -А = 0; (5)

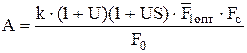. (6)

Решая уравнение(5), получаем два значения для х.В качестве расчетного следует принимать меньшее значение. Если параметр грелки А = 1, то это значит, что горелка работает в оптимальном режиме. Действительно, при А = 1 из уравнения (5) получаем, что х = 1, что соответствует оптимальному режиму (см. формулу (5)). Если А > 1, то уравнение (5) дает мнимые корни. Физически это означает, что горелка не может обеспечить требуемую эжекционную способность. Если А < 1, что соответствует избыточному давлению газа, то в этом случае для сокращения размеров горелки целесообразно за расчетный режим принять неоптимальный режим или применить укороченную эжекционную трубку.

Выходное сечение сопла определяется из уравнения:

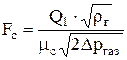. (7)

Порядок конструктивного расчета атмосферной горелки следующий:

1) рассчитывают головную часть горелки и определяют величины значений 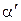, U, d₀, F₀, k₁;

2) по заданному давлению газа находят величину F_с. Принимают определенный вид эжекционной трубки, затем рассчитывают значения А и х;

3) определяют параметры 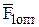, 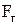и все размеры эжектора.

Пример 10.1. Рассчитать атмосферную горелку (рис. 10.4) производительностью Q = 15 м³/ч, в которой сжигается природный газ с теплотой сгорания 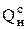= 35128 кДж/м³, ρ_г = 0,72 кг/м³, V₀ = 9,0 м³/м³. Давление газа перед горелкой р_газ = 2,0 кПа.

Рис. 10.4. Схема атмосферной горелки

Решение.

Выбираем расчетные значения основных параметров горелки.

При 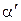= 0,6 выбираем d₀ = 4 мм (см. табл. 10.1). Значение W₀ принимается не более 0,65 предельной скорости, соответствующей отрыву пламени (см. табл. 10.2).

W₀ =0,65∙2,15 = 1,39 м/с.

При этой скорости горелка будет работать с перегрузкой до 2,15 / 1,39 = 1,54 раза.

При значении 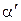= 0,6 проскока пламени не будет, т.к. W_пр.от > W_пр (см. табл. 10.1), т.к. 1,39 > 0,1.

Следовательно, диапазон регулирования горелки составляет 0-1,54 номинальной нагрузки.

Глубину выходных принимаем равной (2÷3) d₀ = 12 мм.

1. Рассчитаем суммарную площадь выходных отверстий:

,

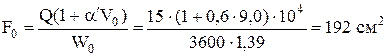где Q - производительность горелки, м³/ч; W₀ - скорость выхода газовоздушной смеси из отверстий горелки, отнесенная к нормальным условиям; V₀ - количество теоретически необходимого воздуха для горения газа, м³/м³.

2. Рассчитаем коэффициент эжекции

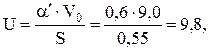
где S = ρ_г / ρ_в =0,72 / 1,29 = 0,55.

3. Определим значения коэффициентов потерь.

Принимаем эжекционную трубку типа (в), представленную на рис. 10.3. Для нее коэффициент потерь эжекционной трубки k = 3.

Значения коэффициентов расхода отверстий горелки μ_о и сопла μ_с принимаем, соответственно, равными 0,8 и 0,9. Температуру подогрева в выходных каналах принимаем t = 100°С.

Рассчитываем коэффициент сопротивления отверстия:

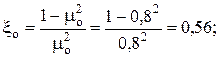
Определяется коэффициент, учитывающий потери энергии в головной части горелки:

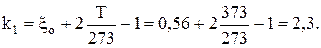
4. Рассчитываем площадь и диаметр сопла

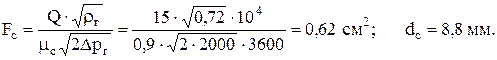
Здесь ρ_г - плотность газа, кг/м³; Δр_г - давление газа перед горелкой, Па.

5. Рассчитываем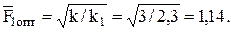

6. Рассчитываем А

А < 1, следовательно, давление газа р_газ = 2,0 кПа больше минимально необходимого. В этом случае за расчетный режим рекомендуется принять неоптимальный режим или использовать укороченную эжекционную трубку. Для сокращения размеров горелки рассчитаем ее на неоптимальный режим. Подставляя значения А получим:

0,584х² - 2х + 0,584 = 0.

Определим 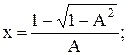х = 0,32.

7. Определяем площадь горловины :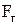

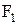= х∙ 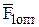= 0,32∙1,14 = 0,36 см²;

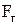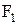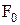= ∙ = 0,36∙192 = 69 см²; d_г = 9,4 см.

Остальные размеры эжектора выбираем по рис. 10.4 как величины, кратные d_г.

Расчет параметров горелки. Для возможности использования однотипных горелок при сжигании в них газов различных составов и при различных давлениях необходимо знать, каким образом изменяются параметры их работы при изменении значений Q_г, S и Δр_газ. Кроме того, нужно выяснить, в какой мере можно влиять на параметры работы горелки изменением одного диаметра сопла, не изменяя при этом конструкции самой горелки.

Из сравнения уравнений (10.2) и (10.6) получаем постоянную горелки С:

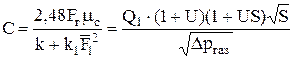. (10.8)

Постоянная горелки С определяется геометрическими характеристикам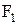и и 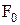, коэффициентами потерь k, k₁, μ_с, но не зависит от поперечного сечения сопла F_c Таким образом, с изменением величины F_c параметры работы горелки будут изменяться так, чтобы постоянная горелки С оставалась неизменной. Уравнение (10.8) позволяет установить влияние отдельных конструктивных размеров горелки на параметры ее работы.

При эксплуатации часто возникает вопрос об определении параметров работы горелки в новых условиях, например, при изменении теплоты сгорания газа или номинального давления с сохранением производительности горелки (последнее достигается изменением сопла). Параметры работы горелки при других эксплуатационных условиях определяют по уравнению постоянной горелки (10.8), по этому же уравнению производят поверочный расчет горелки.

Пример 10.2. Определить параметры работы атмосферной горелки, рассчитанной в примере 10.1, если в ней будет сжигаться коксовый газ со следующими характеристиками: 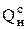= 18000 кДж/м³; S = 0,38; V₀ = 4,4 м³/м³.

Решение.

1. Определим постоянную горелки

.

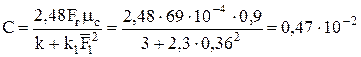2. Тепловая нагрузка горелки равна:

N = Q_гор∙ 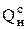= 15∙35128 = 526920 кДж/час,

где Q_гор - производительность горелки на природном газе, м³/час; 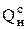- теплота сгорания природного газа, кДж/м³.

Производительность горелки на коксовом газе

Q₁ = N / 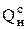= 526920 / 18000 = 29,3 м³/ч.

Коэффициент эжекции при 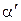= 0,6 равен:

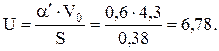
3. Определим необходимое давление газа

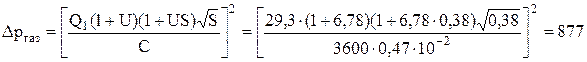Па.

Следовательно, для работы на коксовом газе необходимо давление, равное 877 Па. Если горелка должна работать на большом давлении, следует увеличить производительность горелки или коэффициент эжекции U.

4. Рассчитаем площадь сопла

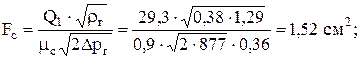d_c ≈ 14 мм.

5. Определим скорость выхода газовоздушной смеси из отверстий горелки

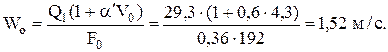
Для коксового газа при величине 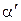= 0,6 проскока пламени нет. Отрыв пламени возможен при скоростях, превышающих 9,75 м/с.

Следовательно, полученная скорость с точки зрения устойчивости горелки является допустимой.