Дифференциальные соотношения в термодинамике
Далее, из определения теплоёмкости процесса имеем
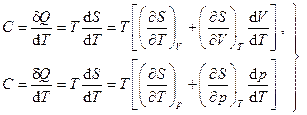
или, используя соотношения Максвелла (5.9),
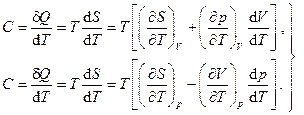
С другой стороны, из (5.13) следует:
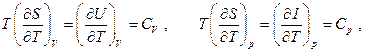
т.е. для теплоёмкости какого-либо термодинамического процесса имеем
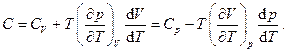 (5.16)
(5.16)
Рассматривая изобарный процесс 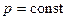 , находим разность теплоёмкостей при постоянном давлении и при постоянном объёме:
, находим разность теплоёмкостей при постоянном давлении и при постоянном объёме:
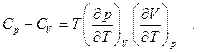 (5.17)
(5.17)
В дальнейшем мы воспользуемся полученными здесь выражениями и рассмотрим также другие примеры использования абстрактного термодинамического метода исследования равновесных систем и обратимых процессов. Применим теперь полученные результаты к идеальному газу. Имеем 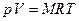 . Отсюда находим производные
. Отсюда находим производные
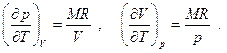 (5.18)
(5.18)
Тогда, используя (5.13), получаем
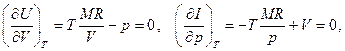 (5.19)
(5.19)
т.е., как и следовало ожидать, для идеального газа внутренняя энергия не зависит от объёма, а энтальпия не зависит от давления. Кроме того, используя определение энтальпии 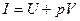 , находим
, находим
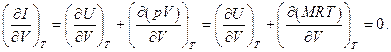
Аналогичным образом находим, что и внутренняя энергия идеального газа не зависит также от давления при постоянной температуре. Далее, из (5.15) с учётом (5.18) получаем
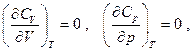 (5.20)
(5.20)
т.е. теплоёмкости идеального газа не зависят от давления и объёма и могут зависеть только от температуры.
Из (5.17) с учётом (5.18) получаем известную формулу Майера для разности теплоёмкостей идеального газа:
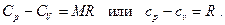
Дата добавления: 2015-12-22; просмотров: 1178;
