Химический потенциал

Пусть однокомпонентная однофазная термодинамическая система является открытой, причём только вещество, составляющее эту систему, может проникать через оболочку. И пусть система является однородной и равновесной.

Очевидно, что изменение внутренней энергии такой системы будет происходить не только вследствие подвода теплоты и совершения над ней работы, но также и вследствие изменения её массы в силу того, что вещество, проникающее через оболочку, несёт с собой свою, присущую ему энергию. Тогда фундаментальные уравнения Гиббса для каждого из четырёх термодинамических потенциалов (5.3) и (5.5) следует дополнить ещё одним слагаемым, пропорциональным изменению массы системы, т.е.

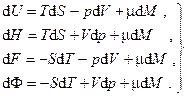(6.1)

Величина μ, определяемая, согласно свойствам полных дифференциалов, частными производными

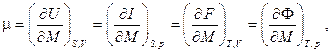(6.2)

носит название химического потенциалаи имеет смысл изменения энергии термодинамической системы при изменении её массы на единицу при поддержании постоянной той или иной пары независимых термодинамических параметров системы.

Найдём связь химического потенциала с другими термодинамическими потенциалами системы. Для этого рассмотрим четвёртое из выражений (6.1). Свободную энергию Гиббса Φ, энтропию S и объём системы V запишем через их удельные величины:

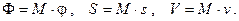
Заменяя дифференциал свободной энергии Гиббса его выражением 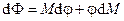и перегруппировав слагаемые, получим

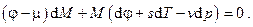
Но согласно (5.5) для M=const=1 кг 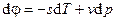, откуда, ввиду произвольности дифференциала массы dM , находим

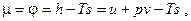(6.3)

т.е. химический потенциал вещества есть его удельная свободная энергия Гиббса. Для идеального газа, используя выражения для энтальпии (2.35) и энтропии (2.44), химический потенциал получим в виде

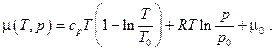(6.4)

Рассмотрим однокомпонентную систему, состоящую из двух взаимодействующих фаз. Пусть каждая из фаз находится в своём внутреннем равновесии, т.е. каждая из них характеризуется своим набором интенсивных и экстенсивных параметров. Изучим вопрос о равновесии между фазами системы. Для этого заключим всю систему в изолирующую оболочку (рис.5.1). Тогда при малом изменении состояния каждой из фаз (подсистем) можно записать для них термодинамические тождества в соответствии с (6.1)

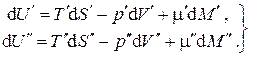(6.5)

В силу аддитивности экстенсивных величин 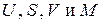, замкнутости системы и обратимости процесса имеем

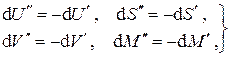
т.е. после почленного суммирования равенств (6.5) получаем

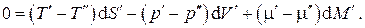
В силу произвольности дифференциалов 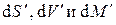множители в скобках при этих дифференциалах должны быть равны нулю, откуда получаем условия термодинамического равновесия двухфазной однокомпонентной системы:

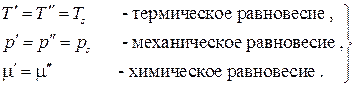(6.6)

Химический потенциал по определению сам является функцией "естественной" пары переменных 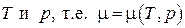, таким образом, условие равновесия фаз может быть записано в виде

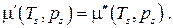(6.7)

Вид функций 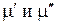от T и p в общем случае различен для каждой из фаз, поэтому условие (6.7) не является тождеством. Это есть алгебраическое уравнение, связывающее температуру и давление в равновесной системе, состоящей из двух сосуществующих взаимодействующих фаз, между которыми имеет место обмен теплотой, работой и веществом.

Таким образом, в двухфазной однокомпонентной системе температура и давление однозначно связаны. Объём же системы может принимать произвольное значение в зависимости от соотношения между массами фаз.

Состояние равновесия двухфазной системы называется состоянием насыщения, а равные для фаз температура и давление - параметрами насыщения 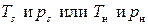(saturation ≡ насыщение).

Рассмотрим аналогичным образом равновесие трёхфазной однокомпонентной системы. Имеем в данном случае:

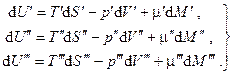(6.8)

Но для замкнутой системы

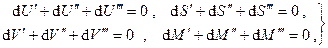
с учётом чего, складывая почленно (6.8), получаем

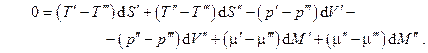
Так как все дифференциалы здесь независимы и значения их произвольны, находим условия равновесия:

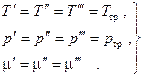(6.9)

Химическое равновесие, т.е. равенство химических потенциалов фаз, может быть записано в виде двух алгебраических уравнений

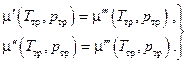(6.10)

Это есть система двух уравнений с двумя неизвестными 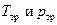. Таким образом, равновесная однокомпонентная система может существовать одновременно в виде трёх фаз только при строго определённых значениях давления и температуры. Такое состояние системы называется тройной точкой.

Совершенно аналогично для равновесной четырёхфазной однокомпонентной системы получим

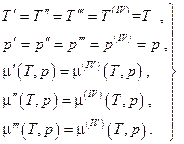(6.11)

В этом случае мы получаем систему трёх уравнений с двумя неизвестными. Такая система уравнений является несовместной за исключением случая, когда любые два из них пропорциональны друг другу, т.е. когда две из четырёх фаз фактически неразличимы, а это уже будет трёхфазная система. Таким образом, в равновесной однокомпонентной системе возможно одновременное сосуществование не более чем трёх фаз. Если равновесная термодинамическая система является многокомпонентной, то число одновременно сосуществующих фаз может быть больше трёх, а именно

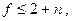(6.12)

где n есть число компонентов системы. Этот результат носит название правила фаз Гиббса.

Известно, что все вещества, в зависимости от условий (давление и температура), могут находиться в трёх агрегатных состояниях: твёрдом, жидком и газообразном. Эти три различных агрегатных состояния ввиду резкого различия их свойств и наличия резкой границы раздела уже могли бы рассматриваться как фазы, однако понятие фазы является более общим, так как жидкое и особенно твёрдое состояния вещества характеризуются при определённых условиях различными физическими свойствами. Но для многих веществ в не очень больших пределах изменения внешних условий понятия агрегатного состояния и фазы совпадают. В дальнейшем под фазами мы будем понимать именно агрегатные состояния.

Если фазовый переход сопровождается выделением или поглощением энергии, то он называется фазовым переходом I рода в отличие от фазовых переходов II рода, которые не сопровождаются поглощением или выделением энергии, а связаны со скачкообразным изменением таких физических свойств как теплоёмкость, тепло- и электропроводность, вязкость и т.д. Примеры фазовых переходов II рода: переход в сверхтекучее или в сверхпроводящее состояние, переход ферромагнетик – парамагнетик и др.

Мы в дальнейшем будем рассматривать только фазовые переходы I рода, во время которых происходит изменение агрегатного состояния, а точнее, переход "жидкость - пар", который весьма часто имеет место в тепловых машинах. Обычно подразумевается, что фазовый переход происходит при постоянном давлении (а значит, и при постоянной температуре), хотя в общем случае это не является обязательным.

Рассмотрим процесс фазового перехода "жидкость – пар". Пусть в цилиндре под поршнем находится 1 кг химически чистой, т.е. без примесей и растворенных в ней газов, жидкости, например воды (рис.6.1). Если пренебречь изменением гидростатического давления в жидкости, вызванного действием силы тяжести, то давление в жидкости будет постоянной по высоте величиной, равной внешнему давлению p. Изобразим состояние жидкости в диаграммах 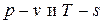точкой а (рис.6.2). Будем медленно (обратимо) подводить к жидкости теплоту через стенки цилиндра. Температура жидкости будет медленно возрастать, объём её также будет увеличиваться, но чрезвычайно мало ввиду малости коэффициента объёмного расширения жидкостей 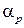. Энтропия жидкости также будет возрастать.