Теплоёмкости идеального газа
Из определений (2.21) и (2.22) находим теплоёмкости при постоянном объёме и при постоянном давлении для идеального газа
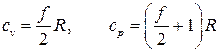 . (2.31)
. (2.31)
Получаемая отсюда разность теплоёмкостей
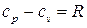 (2.32)
(2.32)
представляет собой известную формулу Майера, а их отношение
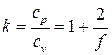 (2.33)
(2.33)
называется показателем адиабатыи, как легко видеть, определяется только числом степеней свободы молекул, т.е. атомностью газа. Результаты расчёта показателя адиабаты для идеального газа на основании молекулярно-кинетической теории представлены в табл.2.1.
Таблица 2.1
| Газ | 1 – атомный | 2 – атомный | 3 – и более атомный |
| Число степеней свободы f | |||
| Показатель адиабаты k | 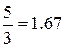
| 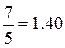
| 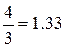
|
Вычисленные по формулам (2.31) значения теплоёмкостей для различных газов сравнительно хорошо совпадают с экспериментально измеренными их значениями в области комнатных температур, которые можно найти в справочной литературе. Расхождение с экспериментом становится существенным при повышении температуры. Эксперимент показывает, что теплоёмкости газов заметно возрастают с увеличением температуры, тогда как рассмотренная выше упрощённая теория даёт для них постоянные значения. Объясняется это расхождение несколькими причинами. Главной причиной расхождения теории с экспериментом является то, что при получении выражения для внутренней энергии газов мы не принимали во внимание квантовые эффекты, учёт которых приводит к тому, что число вращательных и колебательных степеней свободы молекул перестаёт быть постоянной величиной, а зависит от энергии столкновения молекул, т.е., в среднем, от температуры. Кроме того, с увеличением температуры многоатомные молекулы частично диссоциируют, т.е. химический состав газа может заметно измениться.
Из формулы Майера (2.32) и определения показателя адиабаты (2.33) могут быть теоретически найдены удельные теплоёмкости 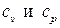 для идеального газа в классическом приближении:
для идеального газа в классическом приближении:
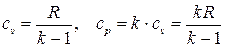 . (2.34)
. (2.34)
Таким образом, в случае идеального газа для внутренней энергии и энтальпии имеем
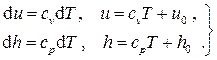 (2.35)
(2.35)
Итак, внутренняя энергия и энтальпия определены с точностью до произвольных постоянных. Обычно энтальпия выбирается равной нулю при температуре 0оС. Тогда, используя связь между энтальпией и внутренней энергией (2.11) и термическое уравнение состояния идеального газа (1.46), получим
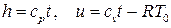 , (2.36)
, (2.36)
где t измеряется в оС, T0=273.15 К.
| Р3.Т8 | Энтропия идеального газа | 0.4 часа |
Запишем выражение первого закона термодинамики в формах (2.9) и (2.18) для идеального газа с учётом (2.35):
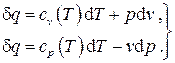 (2.37)
(2.37)
Здесь в свете обсуждённого выше учтено, что теплоёмкости идеального газа в общем случае могут зависеть от температуры.
Каждая из этих дифференциальных форм не является полным дифференциалом, однако в случае идеального газа легко проверить, что умножение их на функцию 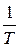 превращает их в полные дифференциалы. В самом деле, учтя уравнение состояния идеального газа
превращает их в полные дифференциалы. В самом деле, учтя уравнение состояния идеального газа 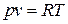 , имеем
, имеем
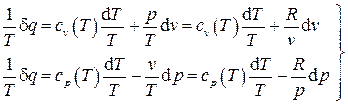 . (2.38)
. (2.38)
Вычисление перекрёстных производных этих дифференциальных форм даёт:
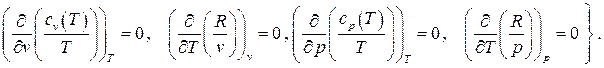
(2.39)
Тождественное равенство перекрёстных производных, согласно признаку (1.4), говорит о том, что дифференциал
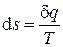 (2.40)
(2.40)
является полным, а величина
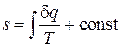 (2.41)
(2.41)
есть некоторая новая функция состояния системы, которая по предложению немецкого учёного Р. Клаузиуса была названа энтропией. Физический смысл энтропии обсудим в главе 4. Из определения дифференциала энтропии (2.40) следует, что, по крайней мере, для идеального газа выражение для количества теплоты может быть записано в форме, аналогичной выражению для работы, т.е. как произведение некоторого потенциала (в данном случае температуры T) на изменение некоторой "координаты" (в данном случае энтропии), т.е.
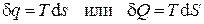 , (2.42)
, (2.42)
а количество теплоты в некотором процессе определится интегралом
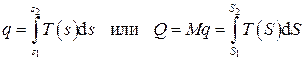 . (2.43)
. (2.43)
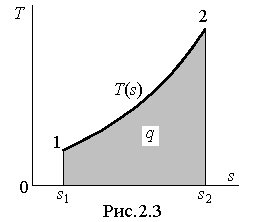
Использование понятия энтропии позволяет ввести в рассмотрение термодинамическую диаграмму T - s, в которой количество теплоты, согласно (2.43), определится площадью под кривой процесса, т.е. графическим изображением заданной зависимости температуры от энтропии 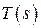 (рис.2.3).
(рис.2.3).
Следует заметить, что экспериментально замерить непосредственно энтропию невозможно, нет приборов, которыми это можно осуществить. Тем не менее энтропию можно вычислить. Например, для идеального газа из формул (2.38) интегрированием находим
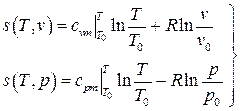 . (2.44)
. (2.44)
Здесь учтено, что энтропия принимается равной нулю при нормальных физических условиях (НФУ).
 |
Относительно формул (2.44) для энтропии идеального газа следует сделать одно замечание: при стремлении абсолютной температуры T к нулю энтропия идеального газа стремится к
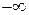 . Объясняется это тем, что при сверхнизких температурах идеальный газ в обсуждённом выше термодинамическом и молекулярно-кинетическом смысле существовать не может. При этих условиях существенную роль начинают играть квантовые закономерности.
. Объясняется это тем, что при сверхнизких температурах идеальный газ в обсуждённом выше термодинамическом и молекулярно-кинетическом смысле существовать не может. При этих условиях существенную роль начинают играть квантовые закономерности.
Дата добавления: 2015-12-22; просмотров: 543;
