Законы идеального газа

Закон Бойля - Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная:

pV = const

при Τ = const, m = const. (7.1)

Кривая, изображающая зависимость между величинами р и V,характеризующими свойства вещества при постоянной температуре, называется изотермой.Изотермы представляют собой гиперболы, расположенные на графике (рис.7.1) тем выше, чем выше температура, при которой происходит процесс.

Законы Гей - Люссака: 1) объем данной массы газа при постоянном давлении изменяется линейно с температурой:

V = V₀(1+αt),

при p = const, и m = const; (7.2)

Рис.7.1. Рис.7.2. Рис.7.3.

2) давление данной массы газа при постоянном объеме изменяется линейно с температурой:

p = p₀(1+ at)

при V = const, т = const. (7.3)

В этих уравнениях t – температура по шкале Цельсия, p₀и V₀— давление и объем при 0°С, коэффициент a= 1/273,15 К^-1.

Процесс, протекающий при постоянном давлении, называется изобарным.На диаграмме в координатах V, t (рис.7.2) этот процесс изображается прямой, называемой изобарой. Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме (рис.7.3) в координатах р, t он изображается прямой, называемой изохорой.

Из (7.2) и (7.3) следует, что изобары и изохоры пересекают ось температур в точке t= -1/a= -273,15 °С, определяемой из условия 1+at= 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина, откуда

Τ = t+1/a.

Вводя в формулы (7.2) и (7.3) термодинамическую температуру, законам Гей-Люссака можно придать более удобный вид:

V= V₀ (1+at) = V₀ [1+a (T-1/a)] = V₀ aТ,

p = (1 + at) = р₀ [1+a (T- 1/)] = p₀ aТ

или

V₁/V₂= Т₁/Т₂

при р = const, m = const, (7.4)

р₁/р₂ = Т₁/Т₂

при V =const, m = const, (7.5)

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной изобаре или изохоре.

Закон Авогадро: моли любых газов при одинаковых температуре и давлении занимают одинаковые объемы.Принормальных условиях этот объем равен 22,41×10^-3 м³/моль.

По определению, в одном моле различныхвеществ содержится одно и то же число молекул, называемое постоянной Авогадро:

N_А =6,022 ^.10²³ моль^-1.

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений р₁, р₂,···, р_п, входящих в нее газов:

p = р₁ + р₂ + ... + р_п.

Парциальноедавление – давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.

7.3.Уравнение Клапейрона – Менделеева

Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р,объемом V и температурой Т. Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением: Рис.7.4.

F(p, V, T)=0,

где каждая из переменных является функцией двух других.

Французский физик и инженер Б. Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля - Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V₁, имеет давление р₁и находится при температуре T₁. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р₂, V₂, Т₂(рис.7.4).

Переход из состояния 1 в состояние 2осуществляется в виде двух процессов: 1) изотермического (изотерма 1 – 1^/ ), 2) изохорного (изохора 1^/ – 2).

В соответствии с законами Бойля— Мариотта (7.1) и Гей-Люссака (7.5) запишем:

р₁V₁=p^/₁V₂, (7.6)

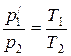. (7.7)

Исключив из уравнений (7.6) и (7.7) p^/₁ получим:

.

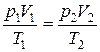Так как состояния 1 и 2были выбраны произвольно, то для данной массы газа величина pV/T остается постоянной, т. е.

pV/T = В = const. (7.8)

Выражение (7.8) является уравнением Клапейрона, в котором В — газовая постоянная, различная для разных газов.

Д. И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (7.8) к одному молю, использовав молярный объем V_m . Согласно закону Авогадро, при одинаковых p и Τ моли всех газов занимают одинаковый молярный объем V_m,поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной. Уравнению

pV_m = RT (7.9)

удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона - Менделеева.

Числовое значение молярной газовой постоянной определим из формулы (7.9), полагая, что моль газа находится при нормальных условиях (р₀=1,013×10⁵ Па, T₀=273,15 К, V_m=22,41×10^-3 м³/моль): R=8,31 Дж/(моль К).

От уравнения (7.9) для моля газа можно перейти к уравнению Клапейрона - Менделеева для произвольной массы газа. Если при некоторых заданных p и T один моль газа занимает молярный объем V_m, то масса т газа займет объем V=(m/М) V_m,где Μ – молярная масса (масса одного моля вещества). Единица молярной массы – килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа

pV = 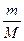RT = vRT,(7.10)

где: v=m/M — количество вещества.

Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана

k=R/N_A= 1,38∙10^-23 Дж/К.

Исходя из этого, уравнение состояния (2.4) запишем в виде

p= RT/V_m = kN_AT/V_m = nkT,

где N_A/V_m=n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения

p=nkT (7.11)

следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1м³ газа при нормальных условиях, называется числом Лошмидта:

N_l = р₀/(kТ₀)= 2,68∙10²⁵ м^-3.