Энтальпия. Полезная внешняя работа. Работа проталкивания
Запишем I закон термодинамики для неподвижной простой системы
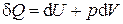
и применим к этому выражению преобразование Лежандра
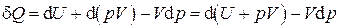 .
.
Здесь под знаком полного дифференциала появляется новая функция состояния

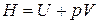 , (2.11)
, (2.11)
называемая энтальпией(старое название - теплосодержание). Таким образом, первое начало термодинамики может быть записано в двух эквивалентных формах:
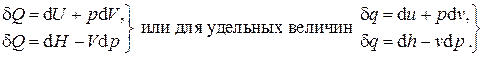 (2.12)
(2.12)
 Физический смысл энтальпии может быть выяснен после выяснения смысла произведения
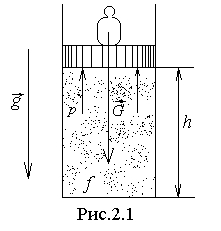
Физический смысл энтальпии может быть выяснен после выяснения смысла произведения 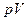 . Для этого рассмотрим следующий частный пример. Пусть в вертикально расположенном цилиндре под поршнем находится газ (рис.2.1). На поршень давит груз весом G=Mгрg. Если груз вместе с поршнем неподвижны, значит, на поршень снизу действует давление со стороны газа, равное
. Для этого рассмотрим следующий частный пример. Пусть в вертикально расположенном цилиндре под поршнем находится газ (рис.2.1). На поршень давит груз весом G=Mгрg. Если груз вместе с поршнем неподвижны, значит, на поршень снизу действует давление со стороны газа, равное 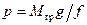 , где f - площадь поршня. Это выражение может быть записано в виде
, где f - площадь поршня. Это выражение может быть записано в виде 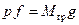 . Умножив левую и правую части этого равенства на высоту h положения поршня от дна цилиндра, получим
. Умножив левую и правую части этого равенства на высоту h положения поршня от дна цилиндра, получим 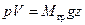 . Произведение же
. Произведение же 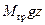 есть потенциальная энергия груза в поле тяжести Земли, рассчитанная по отношению к положению дна цилиндра. Таким образом, произведение pV представляет собой в рассмотренном частном случае потенциальную энергию поршня вместе с грузом, удерживающего газ в заданном объёме V. Можно показать, что и в общем случае, если система удерживается в объёме V, потенциальная энергия оболочки, удерживающей систему, равняется произведению pV. При этом система не обязательно должна быть заключена в физическую оболочку.
есть потенциальная энергия груза в поле тяжести Земли, рассчитанная по отношению к положению дна цилиндра. Таким образом, произведение pV представляет собой в рассмотренном частном случае потенциальную энергию поршня вместе с грузом, удерживающего газ в заданном объёме V. Можно показать, что и в общем случае, если система удерживается в объёме V, потенциальная энергия оболочки, удерживающей систему, равняется произведению pV. При этом система не обязательно должна быть заключена в физическую оболочку.
Таким образом, энтальпию следует понимать как энергию расширенной термодинамической системы, включающей в себя саму систему и оболочку, удерживающую систему в заданном объёме.
В результате преобразования Лежандра кроме энтальпии появилось ещё одно слагаемое 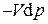 , имеющее смысл дифференциально малого количества некоторой работы
, имеющее смысл дифференциально малого количества некоторой работы 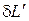 , т.е.
, т.е.
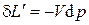 . (2.13)
. (2.13)
Интеграл
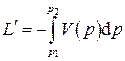 (2.14)
(2.14)
носит название полезной внешней работы (или располагаемой работы). Выясним смысл полезной внешней работы. Работа 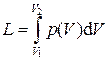 , которую можно назвать работой изменения объёма,представляет собой работу, совершаемую системой против внешних сил. Часть этой работы, называемая работой проталкиванияLпр, затрачивается на изменение потенциальной энергии оболочки и может быть вычислена как разность:
, которую можно назвать работой изменения объёма,представляет собой работу, совершаемую системой против внешних сил. Часть этой работы, называемая работой проталкиванияLпр, затрачивается на изменение потенциальной энергии оболочки и может быть вычислена как разность:
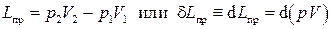 . (2.15)
. (2.15)
Дифференциал этой работы, очевидно, полный. Далее, вычислим разность 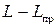 . Удобнее проделать это в дифференциальной форме. Имеем
. Удобнее проделать это в дифференциальной форме. Имеем
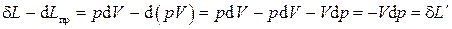 (2.16)
(2.16)
или после интегрирования
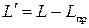 , (2.17)
, (2.17)
т.е. полезная внешняя работа есть разность между работой термодинамической системы и работой проталкивания.
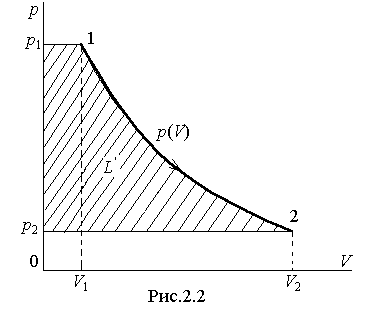
Графически полезная внешняя работа L', определяемая интегралом (2.14), изображается площадью слева от кривой зависимости p(V) в координатах p - V (см.рис.2.2).
 |
Таким образом, первое начало термодинамики для простых систем может быть записано в виде
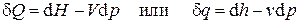 . (2.18)
. (2.18)
Запишем также полный дифференциал удельной энтальпии, выбрав в качестве независимых переменных температуру T и давление p системы:
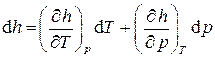 . (2.19)
. (2.19)
| Р3.Т6 | Теплоёмкости термодинамической системы | 0.4 часа |
Запишем математическое выражение первого начала термодинамики для простой системы в двух формах (2.12) (с использованием внутренней энергии и энтальпии) в развёрнутом виде с учётом полных дифференциалов для внутренней энергии (2.10) и энтальпии (2.19) и определения количества теплоты (1.31):
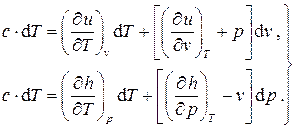 (2.20)
(2.20)
Будем поддерживать постоянным объём системы, т.е. положим 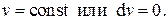 Такой процесс называется изохорным. Тогда, т.к. теплоёмкость системы зависит от процесса, следует положить
Такой процесс называется изохорным. Тогда, т.к. теплоёмкость системы зависит от процесса, следует положить 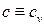 . Из первого уравнения (2.20) получаем
. Из первого уравнения (2.20) получаем
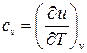 , (2.21)
, (2.21)
т.е. теплоёмкость при постоянном объёме есть изменение внутренней энергии системы при изменении температуры на единицу при поддержании постоянным её объёма. Таким образом, если имеется независимый способ измерения изменения внутренней энергии тела, то теплоёмкость при постоянном объёме определяется экспериментально. Одним из таких независимых способов является, например, измерение джоулева тепла при протекании постоянного электрического тока через сопротивление.
Аналогичным образом, рассмотрев изобарный процесс, т.е. процесс при постоянном давлении, 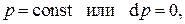 получим определение теплоёмкости при постоянном давлении:
получим определение теплоёмкости при постоянном давлении:
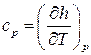 , (2.22)
, (2.22)
т.е. теплоёмкость при постоянном давлении есть изменение энтальпии тела при изменении температуры на единицу при поддержании постоянным давления.
Таким образом, на основании (2.20) теплоёмкость произвольного термодинамического процесса может быть записана в двух эквивалентных формах:
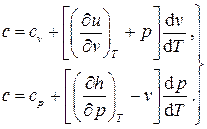 (2.23)
(2.23)
То, что теплоёмкость зависит от процесса, следует из того, что в этих выражениях мы имеем отношения дифференциалов (изменений) двух независимых параметров состояния, которые могут быть произвольными в зависимости от того, как будет организован процесс. В дальнейшем мы рассмотрим частные случаи наиболее употребительных процессов в энергетике.
Обсудим далее первый закон термодинамики в применении к идеальному газу.
| Р3.Т7 | Внутренняя энергия и энтальпия идеального газа | 0.4 часа |
Из молекулярно-кинетического определения идеального газа как совокупности большого числа хаотически движущихся невзаимодействующих материальных точек следует, что единственной формой энергии частиц идеального газа может быть только их кинетическая энергия поступательного движения, вычисленная по отношению к скорости центра масс газа. Тогда под внутренней энергией идеального газа следует понимать суммарную кинетическую энергию поступательного движения частиц, т.е.
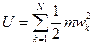 , (2.24)
, (2.24)
где 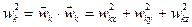 ; N – число частиц; m – масса одной частицы (все частицы предполагаются одинаковыми).
; N – число частиц; m – масса одной частицы (все частицы предполагаются одинаковыми).
Дальнейшее развитие теории и сравнение с экспериментальными данными показало, что точечным частицам истинного идеального газа следует тем не менее приписать наличие внутренней структуры. "Точки" в идеальном газе идентифицируются с атомами; если же газ состоит из многоатомных молекул, т.е. из пространственных структур, то при вычислении внутренней энергии такого газа следует учитывать также энергию вращательного движения молекул и энергию колебаний атомов в молекулах. С учётом этого вместо (2.24) следует записать
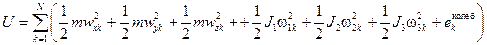 . (2.25)
. (2.25)
Здесь 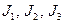 – моменты инерции молекулы относительно её главных осей;
– моменты инерции молекулы относительно её главных осей; 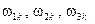 – проекции вектора угловой скорости вращения молекулы на её главные оси. Энергией колебаний атомов в молекулах
– проекции вектора угловой скорости вращения молекулы на её главные оси. Энергией колебаний атомов в молекулах 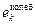 при не очень больших температурах можно пренебречь. Моменты инерции молекулы
при не очень больших температурах можно пренебречь. Моменты инерции молекулы 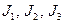 зависят от её конфигурации, т.е. от положения атомов в молекуле, а также от количества атомов в молекулах. Если молекула одноатомная, то все три её момента инерции равны нулю, если молекула двухатомная (или многоатомная с линейным расположением атомов), то один из её моментов инерции (а именно относительно главной оси, проходящей через атомы) равен нулю, а остальные два отличны от нуля и одинаковы. В общем случае трёх- и более атомной молекулы все три момента инерции отличны от нуля и различны. Таким образом, если пренебречь колебаниями атомов в молекулах, каждая из молекул газа может совершать три движения поступательного характера (движение центра инерции молекулы вдоль трёх осей координат x, y, z) и ноль, два или три вращательных движений (соответственно для одно-, двух- или трёх- и более атомных молекул). Как известно из механики, каждое из возможных движений тела носит название степени свободы. Обозначим число степеней свободы молекулы f. Можно сказать, что каждая из степеней свободы молекулы №k обладает энергией
зависят от её конфигурации, т.е. от положения атомов в молекуле, а также от количества атомов в молекулах. Если молекула одноатомная, то все три её момента инерции равны нулю, если молекула двухатомная (или многоатомная с линейным расположением атомов), то один из её моментов инерции (а именно относительно главной оси, проходящей через атомы) равен нулю, а остальные два отличны от нуля и одинаковы. В общем случае трёх- и более атомной молекулы все три момента инерции отличны от нуля и различны. Таким образом, если пренебречь колебаниями атомов в молекулах, каждая из молекул газа может совершать три движения поступательного характера (движение центра инерции молекулы вдоль трёх осей координат x, y, z) и ноль, два или три вращательных движений (соответственно для одно-, двух- или трёх- и более атомных молекул). Как известно из механики, каждое из возможных движений тела носит название степени свободы. Обозначим число степеней свободы молекулы f. Можно сказать, что каждая из степеней свободы молекулы №k обладает энергией 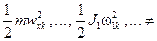 соответственно, причём эта энергия хаотическим образом меняется с течением времени вследствие столкновений молекул. Австрийский физик Людвиг Больцман в конце XIX века методами статистической физики доказал так называемую теорему о равнораспределении энергиипо степеням свободы, согласно которой в среднем при хаотическом движении в равновесии на каждую степень свободы молекулы приходится одинаковая энергия, равная
соответственно, причём эта энергия хаотическим образом меняется с течением времени вследствие столкновений молекул. Австрийский физик Людвиг Больцман в конце XIX века методами статистической физики доказал так называемую теорему о равнораспределении энергиипо степеням свободы, согласно которой в среднем при хаотическом движении в равновесии на каждую степень свободы молекулы приходится одинаковая энергия, равная 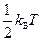 , где
, где 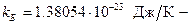 постоянная Больцмана. На основании теоремы о равнораспределении выражение для внутренней энергии идеального газа (2.25) можно записать в более простой форме:
постоянная Больцмана. На основании теоремы о равнораспределении выражение для внутренней энергии идеального газа (2.25) можно записать в более простой форме:
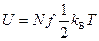 . (2.26)
. (2.26)
Количество молекул N можно вычислить как произведение числа киломолей ν газа и числа Авогадро NA, в свою очередь число киломолей может быть подсчитано делением массы газа M на молекулярную массу газа μ, определяемую его химической формулой. Таким образом, (2.26) принимает вид
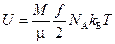 . (2.27)
. (2.27)
Используя численные значения числа Авогадро и постоянной Больцмана, находим 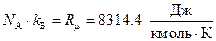 , т.е. это произведение в точности равно универсальной газовой постоянной. Окончательное выражение для внутренней энергии идеального газа имеет, следовательно, вид
, т.е. это произведение в точности равно универсальной газовой постоянной. Окончательное выражение для внутренней энергии идеального газа имеет, следовательно, вид
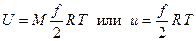 , (2.28)
, (2.28)
где учтено определение газовой постоянной (1.45).
Энтальпия идеального газа легко находится из определения (2.11) и термического уравнения состояния (1.46):
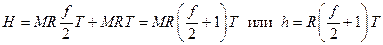 . (2.29)
. (2.29)
Как и следовало ожидать, внутренняя энергия и энтальпия для идеального газа зависят только от температуры и не зависят ни от объёма, ни от давления, т.е. для идеального газа имеем:
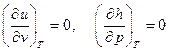 . (2.30)
. (2.30)
Это объясняется отсутствием взаимодействия между молекулами идеального газа.
Дата добавления: 2015-12-22; просмотров: 4338;
