Течение газов с трением

В реальных условиях течение газов в каналах сопровождается диссипацией энергии вследствие трения, обусловленного вязкостью среды и шероховатостью стенок канала (в турбулентном режиме движения). Поэтому в уравнение Эйлера необходимо ввести член, учитывающий удельные силы трения

.

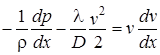После преобразований с использованием уравнения Менделеева-Клапейрона получим

Имея в виду, что

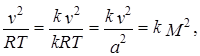
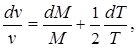
и привлекая уравнение сплошности в логарифмических дифференциалах, которое для каналов с постоянной площадьюпоперечного сечения имеет вид

найдем

.

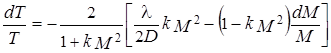Но из уравнения энергетического баланса при адиабатном течении газа

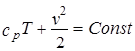
следует

С учетом этого

.

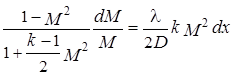Интегрирование дает

.

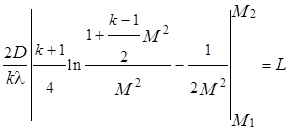Критическая длина, на которой достигается скорость звука, равна

.

Температуру и давление на выходе трубопровода определяют по формулам

; .

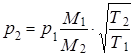В качестве примера определим потери давления при адиабатном течении воздуха в пневмолинии диаметром D =0,01м и длиной L=20м, если расход составляет G =0,189 кг/c, температура и давление на входе T1 =300K,
р1 = 0,6 МПа. Эквивалентную шероховатость трубопровода примем равной D=0,01 мм.

На входе плотность и скорость воздуха, скорость звука, число Маха и число Рейнольдса равны

.

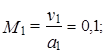
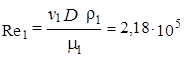Коэффициент сопротивления по длине по условиям на входе по формуле Альтшуля

.

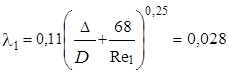Число Маха на выходе, определенное методом последовательных прибли-жений

.

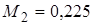Остальные параметры на выходе

Т₂ = 297,6 К; а₂ = 347 м/с; v₂ = 78,1 м/с; Re₂ = 4,88×10⁴; l₂ = 0,024.

Уточненные результаты расчетов по среднему значению коэффициента сопротивления по длине lср=0,026:

Т₂ = 298,3 К; а₂ = 347,4 м/с; v₂ = 68,8 м/с.

Сопротивление пневмолинии

Dр = 0,298 МПа.

Часто встречающейся задачей является определение пропускной спо-собности трубопровода заданных размеров при наполнении и опорожнении емкостей по заданным значения давления на концах и температуры на входе. Решается она в следующей последовательности:

– по температуре, давлению и начальной оценке числа Маха на входе находят скорость звука, скорость потока и по уравнению состояния плотность газа;

– по уравнению неразрывности рассчитывают расход газа по условиям на входе;

– по приведенным выше соотношениям определяют число Маха, тем-пература, скорость звука и скорость потока на выходе;

– по полученной температуре и заданному давлению находят по урав-нению состояния плотность газа на выходе;

– рассчитывают расход газа по условиям на выходе;

– подгонкой числа Маха на входе выравнивают значения расходов на концах трубопровода.

При изотермическом движении газа число Маха на выходе определяют решением уравнения

.

Давление равно

.

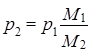С исходными данными, использованными в рассмотренном выше примере, результаты расчетов практически совпадают.

При адиабатном течении газов с трением в каналах с переменной площадью поперечного сечения также действует приведенное выше уравнение движения, но с учетом того, что уравнение неразрывности имеет вид

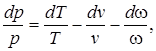
изменение числа Маха по длине канала описывают дифференциальным уравнением

дополнительно содержащим функцию ω(x), которая характеризует форму канала и может иметь самый разный вид, в том числе не позволяющий провести непосредственное интегрирование. В такой ситуации, а также при необходимости учета изменения коэффициента сопротивления по длине, приходится прибегать к конечно-разностным методам расчета течения.

После выбора шага разбиения канала на участки Dх параметры на выходе каждого из них определяют по соотношениям

.

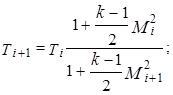
В качестве примера определим длину сопла с экспоненциальным про-филем, диаметр на выходе, скорость и противодавление, соответствующие критическому режиму истечения воздуха, если на входе диаметр равен
D1=30 мм, давление р1=0,6 МПа, температура T1=300K, скорость v1=35 м/c. Коэффициент трения по длине постоянен и равнен l=0,025.

Пусть профиль сопла описывают уравнением

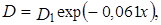
где х – расстояние от входа в сопло.