Основы моделирования гидравлических явлений
Адекватное математическое описание гидравлических явлений и объектов с получением аналитического или численного решения во многих случаях не представляется возможным. Поэтому важную роль в гидравлике играют экспериментальные исследования. В частности, вся информация по сопротивлению при турбулентном движении жидкости получена именно таким путем.
С целью экономии средств или при невозможности проведения экспери-ментов на реальных объектах, как например при проектировании крупных гидротехнических сооружений, исследуют модели таких объектов, выпол-няемые в уменьшенном масштабе. При этом моделирование должно осуще-ствляться так, чтобы полученные результаты, выводы и рекомендации можно было перенести на натуру. Достигается это обязательным соблюдением тре-бований теории подобия, в соответствии с которой геометрические, кине-матические и динамические характеристики макета и оригинала должны находиться в определенных соотношениях.
Геометрическое подобие выполняется, если отношение всех сходствен-ных размеров одинаково
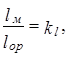
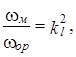
 .
.
Для кинематического подобия необходимо, чтобы траектории движения сходственных частиц жидкости были геометрически подобны и одинаково ориентированы, а отношения скоростей и ускорений в сходственных точках макета и оригинала одинаковыми
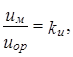
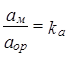 .
.
В геометрически и кинематически подобных объектах масштаб времени определяется выражением
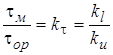 .
.
 |
Динамическое подобие соблюдается, если в любой паре сходственных точек макета и оригинала действуют одноименные и одинаково ориенти-рованные силы, а отношение всех сил одинаково
Так, например, отношение сил инерции в макете и оригинале должно быть равно отношению равнодействующей всех сил
 |
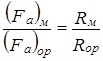 .
.
В соответствии со вторым законом Ньютона
 |
С учетом этого
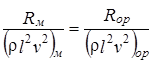 .
.
Безразмерный комплекс
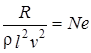 .
.
получил название числа Ньютона. В механически подобных системах эти числа должны быть одинаковыми.
 |
Во многих случаях рядом несущественных сил можно пренебречь и вместо равнодействующей использовать определяющую силу. Если такой силой является сила трения, то в соответствии с законом Ньютона для внутренного трения
 |
число Ньютона равно
 |
а обратная ему величина, называемая критерием Рейнольдса, составляет
 |
По смыслу этот критерий характеризует отношение сил инерции к силам трения.
 |
Если преимущественное значение имеют силы тяжести, как при истече-нии жидкости из отверстий и насадок,
 |
то определяющим является критерий Фруда
 |
который характеризует отношение сил инерции к силам тяжести.
 |
При движении жидкости в трубопроводах на нее действуют торцовые силы давления, равнодействующая которых равна
 |
Подстановка в число Ньютона дает безразмерный комплекс, называемый критерием Эйлера
 |
который характеризует отношение сил давления к силам инерции.
При одновременном действии нескольких сил условием подобия макета и образца является равенство всех частных критериев подобия. На практике, однако, это требование часто удовлетворить не удается и приходится опери-ровать критериями, соответствующими превалирующим силам.
 |
В качестве примера найдем по результатам исследования модели потери давления в проектируемом магистральном водоводе диаметром D = 1,2 м и длиной L= 5000 м при расходе воды Q = 0,5 м³/с.
Скорость движения воды в оригинале

 |
Критерий Рейнольдса
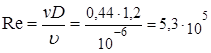 .
.
Для получения такого же числа Рейнольдса в модели водовода диаметром d=50 мм скорость движения воды должна составлять
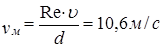 .
.
 |
Измеренные в опыте потери давления в модельном трубопроводе длиной l=1 м оказались равными 129 кПа. Этому соответствует число Эйлера
 |
В геометрически подобном участке водовода длиной D/d=24 м с таким же значением критерия Эйлера потери давления составят
 |
Общие потери давления в водоводе равны 5000/24×0,223= 46,5 кПа.
Вопросы для проверки усвоения материала
1. Чем отличаются уравнения Эйлера в гидростатике и гидродинамике?
2. Какие условия однозначности привлекаются для решения диффе-ренциальных уравнений движения жидкости?
3. От чего зависит положение пьезометрической линии при движении жидкости?
4. Какой вид имеют уравнения сохранения энергии придвижении иде-альной и реальной жидкости?
5. Чем отличаются напорные линии при движении идеальной и реальной жидкости?
6. От чего зависят потери напора при ламинарном и турбулентном движении жидкости?
7. Возможен ли гидравлический удар при резком торможении потока несжимаемой жидкости в абсолютно жестком трубопроводе?
8. С какой целью применяют насадки при опорожнении емкостей с жидкостью.
9. Когда использование цилиндрических насадок становится неэффек-тивным?
Дата добавления: 2015-11-26; просмотров: 1344;
