Операция логического следования (импликации)

Логическое следование (импликации) образуется соединением двух высказываний в одно с помощью оборота речи «если…., то….»

Логическая операция импликации «если А, то В», обозначается А®В.

Истинность такого высказывания задается специальной таблицей, таб­лицей истинности:

Составное высказывание, образованное с помощью операции логического следования (импликации), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).

Логическое равенство (эквивалентность).

6)

Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда».

Логическая операция эквивалентность «А тогда и только тогда, когда В» обозначается А~В.

Истинность такого высказывания задается специальной таблицей, таб­лицей истинности:

Составное высказывание, образованное с помощью логической операции эквивалентность истинно тогда и только тогда, когда оба высказывания либо истины, либо ложны.

Законы логики

Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений.

Закон	Выражение
Закон тождества	А=А
Закон непротиворечия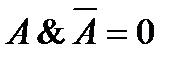
Закон исключения третьего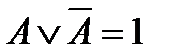
Закон двойного отрицания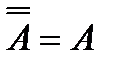
Закон де Моргана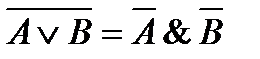
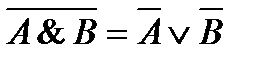
Закон коммутативности	А&B=B&A
Закон ассоциативности
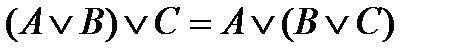
Закон дистрибутивности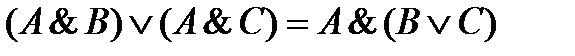

«Технические средства информационных технологий»