Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией логического отрицанияилиинверсией.
Инверсия делает истинное высказывание ложным и наоборот.
Операцию логического отрицания (инверсию) над логическим высказыванием А принято обозначать Ā. Образуем высказывание С , являющееся логическим отрицанием А:С=Ā
Истинность такого высказывания задается специальной таблицей, таблицей истинности логического отрицания:
| А | Ā |
| 0 | 1 |
| 1 | 0 |
В рассмотренном нами выше примере А = 1, т.е. полученное в результате логического отрицания высказывание «Не два умножить на два равно четырем» ложно.
Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую войдут символы, обозначающие высказывания и их отрицания, соединенные знаками логических операций. Правила преобразования логических выражений, аналогичны правилам алгебры.
При преобразовании логических выражений определено следующее старшинство логических операций: инверсия, конъюнкция, дизъюнкция (для изменения указанного порядка могут использоваться скобки).
Высказывания, у которых таблицы истинности совпадают, называютсяравносильными.Для обозначения равносильных высказываний используется знак «=».
Пусть имеются простые высказывания А,В. Докажем, что сложное
высказывание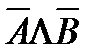 
равносильно сложному высказыванию 
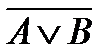. Построим сначала таблицу истинности для логических выражений 
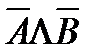и :
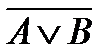| А | В |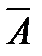 
| 
|
|
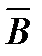
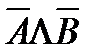
| А | В |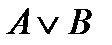 
|
|
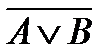
| l | |||
| l |
Таблицы истинности совпадают, следовательно, логические выражения равносильны: =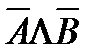
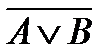
Дата добавления: 2015-12-22; просмотров: 1064;