Минимизация логистических рисков, уменьшение влияния от внешних факторов
Современный логистический менеджер, кроме критерия сокращения издержек, должен помнить и о задаче управления логистическими рисками. Разумеется, не представляется возможным одновременно минимизировать логистические издержки, снижать риски потерь и длительность логистического цикла, поэтому профессионализм специалиста по логистике будет выражаться, прежде всего, в нахождении оптимального баланса между этими параметрами.
Рассмотрим страховые методы и возможность их применения при реализации коммуникационных и интеграционных процессов в сервисной деятельности с целью упреждения логистических рисков.
Любое существующее предложение страхового контракта с точки зрения ЛПР можно охарактеризовать, прежде всего, следующими атрибутами:
Страховая сумма (оговоренная в контракте сумма возмещения, выплачиваемая страховой компанией страхователю-ЛПР при наступлении оговоренного конкретного страхового случая).
Страховая премия (сумма, выплачиваемая страхователем-ЛПР в пользу страховой компании при заключении страхового контракта).
Страховой тариф (отношение страховой суммы к цене страхового полиса, показывающее, какая компенсация гарантируется ЛПР на каждую вложенную в цену страхового полиса денежную единицу при наступлении оговоренного страхового случая).
При принятии решения необходимо учитывать и такой параметр, как условия страхования – свод правил, определяющих, по каким именно рискам страховщик несёт ответственность перед страхователем. Ниже приведен один из примеров классификации:
"С ответственностью за все риски".
"С ответственностью за частную аварию".
"Без ответственности за повреждения, кроме случаев крушения".
Нередко страховые компании предлагают клиентам за дополнительную плату застраховать дополнительные риски, не покрываемые стандартными условиями страхования, например, военные и забастовочные риски, хищение груза, риски, связанные с погрузочно-разгрузочными работами и т.д.
Не может не обратить на себя и экономическая привлекательность страхования: так, согласно статьям 263, 270 НК РФ, взносы по добровольному страхованию грузов могут быть в полном объёме отнесены на расходы отчётного периода (следовательно, они уменьшают налогооблагаемую прибыль компании).
Рассмотрим две модели управления логистическими рисками в цепи поставок, предложенные Ануреевым Е.А.
Модель для двух сценариев
Пусть интересующее ЛПР преобразование его начального капитала 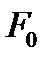 в конечный случайный результат Ff характеризуется преобразованием требуемых затрат
в конечный случайный результат Ff характеризуется преобразованием требуемых затрат 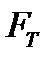 в соответствующий случайный доход FД:
в соответствующий случайный доход FД:
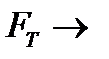 FД,
FД,
причем затраты 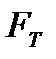 известны и фиксированы. Например, если речь идет о поставке партии товара, то объём партии оговорен и не подлежит изменению.
известны и фиксированы. Например, если речь идет о поставке партии товара, то объём партии оговорен и не подлежит изменению.
Рассмотрим простейшую условную ситуацию, когда в рамках модели управления рисками для случайного дохода FД требуется учитывать и анализировать только два сценария (более общая модель будет рассмотрена ниже). А именно:
1. Благоприятное развитие событий (вероятность чего обозначим через 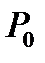 ), когда FД = FТ + FПН, где FПН – заранее известная прибыль, на которую может рассчитывать ЛПР в случае удачной реализации проекта;
), когда FД = FТ + FПН, где FПН – заранее известная прибыль, на которую может рассчитывать ЛПР в случае удачной реализации проекта;
2. Неблагоприятное развитие событий (вероятность 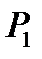 ), когда FД = 0. Схематическое представление для преобразования затрат ЛПР в рамках такой упрощённой модели даёт верхняя часть рис. 1, где через FПН обозначена величина прибыли, соответствующая наиболее благоприятному сценарию развития событий.
), когда FД = 0. Схематическое представление для преобразования затрат ЛПР в рамках такой упрощённой модели даёт верхняя часть рис. 1, где через FПН обозначена величина прибыли, соответствующая наиболее благоприятному сценарию развития событий.
Наличие на рынке предложения от страховой компании означает, что для ЛПР имеется возможность вкладывать свой капитал (дополнительно к тем вложениям, которые требует соответствующий бизнес) также в предложение страховой компании, которое характеризуется преобразованием, представленным в нижней части рис. 1. При этом в рамках указанного преобразования использованы обозначения: Р – цена страхового полиса; q – отношение величины страхового возмещения к цене страхового полиса для данного типа контрактов, оговариваемое страховой компанией.
Рис. 1. Преобразование суммарных затрат ЛПР (модель I) для синтезированного предложения с учетом страхования (два сценария)
Таким образом, в рамках рассматриваемой модели найденная безрисковая стратегия для ЛПР в портфельном представлении характеризуется именно безрисковым портфелем ( 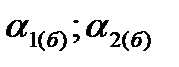 ), где параметры такого портфеля определяются приведенными выше равенствами.
), где параметры такого портфеля определяются приведенными выше равенствами.
Найдем теперь показатель 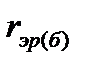 безрисковой рентабельности применительно к такой стратегии управления рисками. Этот показатель определяется преобразованием в рамках соответствующей схемы «Деньги – Товар/Услуга – Деньги»:
безрисковой рентабельности применительно к такой стратегии управления рисками. Этот показатель определяется преобразованием в рамках соответствующей схемы «Деньги – Товар/Услуга – Деньги»:
| Товар/Услуга |
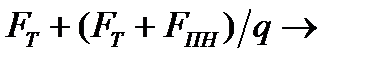
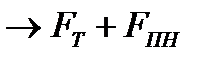
Для показателя 1+ 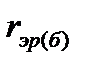 , очевидно, имеем
, очевидно, имеем
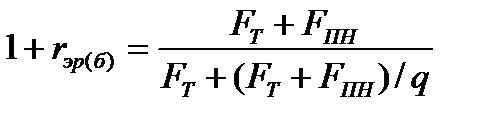
Воспользовавшись равенством 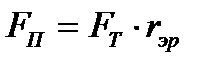 , после несложных преобразований получаем
, после несложных преобразований получаем
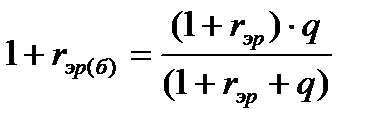
Как видно, имеет место следующее соотношение, связывающее показатель 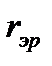 и интересующий нас показатель
и интересующий нас показатель 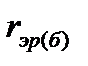 :
:
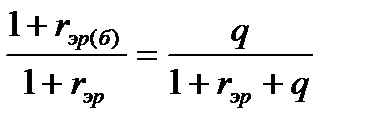
Это соотношение показывает, что безрисковая рентабельность 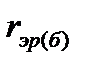 реализации соответствующего предложения в бизнесе за счёт использования страхового контракта будет, естественно, несколько меньшей (знаменатель в правой части последнего равенства оказался больше, чем числитель), чем рентабельность
реализации соответствующего предложения в бизнесе за счёт использования страхового контракта будет, естественно, несколько меньшей (знаменатель в правой части последнего равенства оказался больше, чем числитель), чем рентабельность 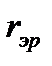 без страхования, но только в расчёте на благоприятный исход, т.е. только применительно к ситуации, когда страховой случай не наступит (другими словами, в расчёте на то, что ЛПР повезёт).
без страхования, но только в расчёте на благоприятный исход, т.е. только применительно к ситуации, когда страховой случай не наступит (другими словами, в расчёте на то, что ЛПР повезёт).
Модель для множества сценариев
Вернёмся к рассмотренной упрощённой модели I управления рисками на основе страхования. Обобщим представленную модель для случая произвольного числа сценариев. Например, если речь идёт о поставке определенной партии товара, то соответствующие сценарии могут включать не только «крайние» случаи (поставка всей партии; полная утрата товара). А именно, пусть далее Δ обозначает долю утраченного товара ( 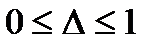 ) от всего объема партии. При этом, если:
) от всего объема партии. При этом, если:
Δ = 0 (наиболее благоприятное развитие событий, вероятность чего обозначаем снова через 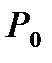 ), то FД =
), то FД = 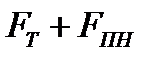 ;
;
Δ = 1 (исключительно неблагоприятное развитие событий, вероятность чего обозначаем через 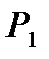 ), то FД = 0;
), то FД = 0;
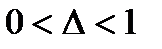 (частично неблагоприятное развитие событий, вероятность чего обозначаем через
(частично неблагоприятное развитие событий, вероятность чего обозначаем через 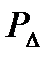 ), то FД =
), то FД = 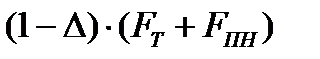 .
.
Соответствующее схематическое представление этих сценариев даёт рис. 3.
Рис. 3. Преобразование затрат бизнеса ЛПР при сценариях,
зависящих от доли ∆ утраченного товара.
Естественно, предлагаемый страховой контракт для ЛПР также должен учитывать соответствующие сценарии. Другими словами, правильно оформленный страховой контракт должен предусматривать страховые выплаты FСВ в зависимости от реализуемого сценария для Δ. А именно, если:
Δ = 0 (благоприятное развитие событий, вероятность чего обозначаем снова через 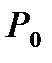 ), то FСВ = 0 (выплаты не предусматривается);
), то FСВ = 0 (выплаты не предусматривается);
Δ = 1 (исключительно неблагоприятное развитие событий, вероятность чего обозначаем через 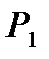 ), то FСВ =
), то FСВ = 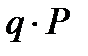 (полное страховое возмещение);
(полное страховое возмещение);
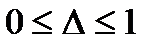 (частично неблагоприятное развитие событий, вероятность чего обозначаем через
(частично неблагоприятное развитие событий, вероятность чего обозначаем через 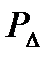 ), то FСВ =
), то FСВ = 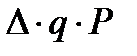 (страховые выплаты составляют именно долю Δ от полного страхового возмещения).
(страховые выплаты составляют именно долю Δ от полного страхового возмещения).
Такое преобразование затрат Р (издержки ЛПР на цену страхового полиса), связанное с указанным оформлением страхового контракта, представлено на рис. 4.
Рис. 4. Преобразование для затрат ЛПР на покупку страхового полиса при сценариях, зависящих от доли ∆ утраченного товара
Очевидно, что для рассматриваемого обобщения модели страхования рисков, два «предложения» для ЛПР, представленные схематически на рис. 3 – 4, связаны совершенной отрицательной корреляционной связью (случай 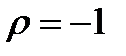 ). Соответственно все выводы, сделанные для упрощённой модели, останутся прежними. В частности, ЛПР может синтезировать безрисковую стратегию реализации предложения в своём бизнесе на основе использования страхового контракта. Структура такого синтезированного «предложения» (на основе предложений, представленных преобразованиями его капитала на рис. 3 – ) приведена на рис. 5.
). Соответственно все выводы, сделанные для упрощённой модели, останутся прежними. В частности, ЛПР может синтезировать безрисковую стратегию реализации предложения в своём бизнесе на основе использования страхового контракта. Структура такого синтезированного «предложения» (на основе предложений, представленных преобразованиями его капитала на рис. 3 – ) приведена на рис. 5.
Рис. 5. Преобразование суммарных затрат ЛПР с учётом
покупки страхового контракта (сценарии определяются
долей ∆ утраченного товара)
Рис. 5 показывает, что преобразование суммарных затрат ( 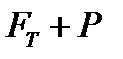 ) ЛПР будет безрисковым тогда и только тогда, когда будет выполнено равенство, приведенное ранее применительно к упрощенной модели
) ЛПР будет безрисковым тогда и только тогда, когда будет выполнено равенство, приведенное ранее применительно к упрощенной модели
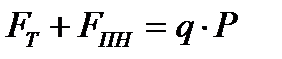
Действительно, при сценарии Δ = 0 окончательный суммарный результат для ЛПР (т.е. результат бизнеса плюс выплаты страховой компании) определён и составляет
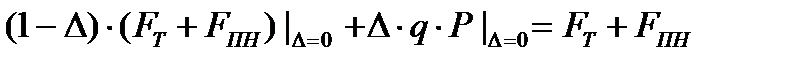
Кроме того, для другого «крайнего» сценария Δ = 1 окончательный суммарный такой результат для ЛПР (при выборе Р в соответствии с указанным выше равенством) также будет определён и составит
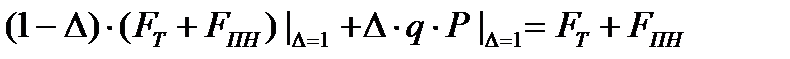
Аналогично, при любом 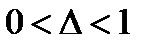 также получим, что окончательный суммарный результат для ЛПР (с учетом равенства
также получим, что окончательный суммарный результат для ЛПР (с учетом равенства 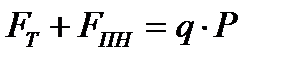 ) будет тем же
) будет тем же
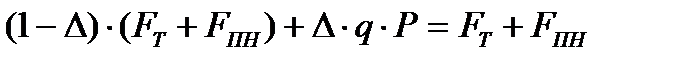
Таким образом, в рамках рассматриваемой обобщённой модели управления рисками на основе страхования, как и в предыдущем упрощённом случае, безрисковая стратегия для ЛПР требует заключения страхового контракта с ценой возмещения 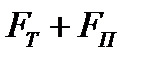 . При этом цена страхового полиса в рамках такой безрисковой стратегии, гарантирующей безрисковый результат для ЛПР, составит (как и в случае упрощенной модели с двумя сценариями):
. При этом цена страхового полиса в рамках такой безрисковой стратегии, гарантирующей безрисковый результат для ЛПР, составит (как и в случае упрощенной модели с двумя сценариями):
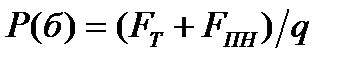
Дата добавления: 2015-12-22; просмотров: 1133;
