Матрица А: парные сравнения
| … | j | ... | n | |||
| … i … n | — x21 xi1 xn1 | x12 — xi2 xn2 | x1j x2j xij xnj | x1n x2n xin — |
Каждый эксперт, заполняющий такую матрицу, должен проставить на пересечении строки и столбца для двух сравниваемых факторов оценку хij. В зависимости от того, является ли фактор i более предпочтительным, чем фактор j, эта оценка равна 1 или 0 соответственно. В главной диагонали такой матрицы проставляются прочерки или нули. Каждая пара факторов может сравниваться единожды или дважды (например, сначала х12, а затем х21 в матрице табл. 7.7). В случае когда факторы сравниваются попарно дважды (полное парное сравнение), общее число сравнений I = п(п — 1); при однократном попарном сравнении
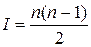, (7.8)
где п — общее число факторов.
Существуют различные варианты частичного парного сравнения. Так, эксперту могут предложить сравнить заранее сгруппированные пары факторов, где он должен лишь указать наиболее предпочтительный; в этом случае каждый фактор сопоставляется только с каким-либо другим.
Может быть заранее подготовлена матрица частичного парного сравнения, в которой одна группа факторов сопоставляется со всеми другими, тогда как остальные факторы сопоставляются лишь с некоторыми другими.
Метод парных сравнений может быть использован и для установления суммарных рангов факторов. С этой целью факторы, которые должны быть проранжированы, записываются в обычном порядке в левом столбце и в верхней строке матрицы, а затем производится их парное сравнение. Матрица просматривается слева направо. Когда обнаруживается, что фактор, находящийся в левом столбце матрицы, предпочтительнее, чем фактор, помещенный в верхней строке, то в верхнюю часть клетки, образованной пересечением строки и столбца, ставится 1, а в нижнюю — 0. Если фактор, находящийся в верхней строке матрицы, предпочтительнее, чем фактор в левом столбце, то 0 ставится в верхнюю половину клетки, а 1 — в нижнюю. Затем, в зависимости от числа предпочтений, каждому фактору присваивается определенный ранг. Так, в приведенной в качестве примера матрице (табл. 7.8) фактор С получает наивысший ранг - 3, фактор D — ранг 2, фактор А — 1 и фактор В — 0.
Таблица 7.8.
Дата добавления: 2015-12-22; просмотров: 856;