Математические методы и расчеты, используемые в экономических исследованиях
В микроэкономике с конца XIX века широко используется предельный (маржинальный, от англ. «marginal» – предельный) анализ, когда процесс производства или потребления, спрос, предложение представляются в виде соответствующей функции, зависящей от набора экономических переменных (факторов – труд, капитал, цены, доходы и т.д.). Чтобы выявить количественное влияние на конечный результат (функцию) того или иного фактора, можно использовать инструменты математического анализа через вычисление предела функции при бесконечно малом приращении аргумента (фактора), т.е. продифференцировав функцию по соответствующему фактору. На практике приходится рассчитывать предельный доход, предельные издержки, предельный продукт труда или капитала, предельную ставку налогообложения, предельную производительность и т.д. Например, производственная функция, показывающая зависимость выпуска продукции (Q) фирмой от затрат труда и капитала (L, K):
Q=3∙L½∙K½ или Q= 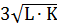
Тогда предельный продукт труда, показывающий, каким будет прирост производства ∆Q, если затраты труда (количество работников или фонд заработной платы) увеличится на единицу составит:
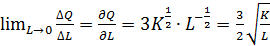 .
.
Предельный анализ и дифференцирование позволяют найти максимальное и минимальное значение функции, что является определяющим для нахождения оптимума фирмы по выпуску или по затратам. Для этого нужно решить задачу на нахождение экстремума функции через ее дифференцирование по соответствующему фактору и приравнять полученную производную нулю.
Допустим, общая полезность в каких-то единицах от потребления количества продуктов Х равна TU=16х–х2. Определить то количество потребляемых продуктов, которое обеспечивает максимальную полезность.
Условие нахождение max TU(x) будет:  , т.е.
, т.е.
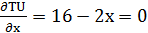 , откуда х=8.
, откуда х=8.
| Рис. 1. График функции TU=16x-x2 полезности |
| TU=16х-х2 |
| TU |
| х |
Очень важным в практическом отношении нахождение процентного изменения функции (выпуска продукции, выручки, спроса или предложения) при однопроцентном изменении какого-то фактора (цены, дохода). Это проблема определения эластичности функции, которая также решается через аппарат дифференцирования. Полученные таким образом коэффициенты эластичности позволяют смоделировать, например, функцию реального спроса на продукцию фирмы в зависимости от изменений цены на нее, от изменений цен на товары-заменители и дополняющие товары, от изменений доходов потребителей, от расходов на рекламу.
При рассмотрении потребительского выбора и принятия решений в условиях рыночной конкуренции широко используется теория множеств и теория игр. Действительно, рыночное взаимодействие фирм, их экономическое поведение можно представить как кооперативную (с элементами взаимного сотрудничества, соглашений, коалиций) или некооперативную игру на получение выигрыша (максимального дохода, например). Интересно, что у истоков теории игр стояли такие математические гении как Д. Нейман (один из «отцов» кибернетики, компьютера, атомной бомбы и т.д.) и Д. Нэш, получивший Нобелевскую премию по экономике и сформулировавший фундаментальную концепцию равновесия в экономической игре, которое сейчас самые крупные экономисты-теоретики сравнивают с открытием структуры ДНК в биологии (знаменательно, что эти открытия были сделаны практически одновременно – в 1951 году).
Следует отметить особое значение линейной алгебры и линейного программирования для нахождения оптимума сложных экономических функций с множеством переменных (факторов). Аппарат системы простых линейных уравнений, составление соответствующих матриц коэффициентов и операции с ними, позволяют найти единственные решения, т.е. найти необходимые цены, выпуски продукции, которые обеспечивают устойчивое равновесие, максимальную доходность.
В расчетах экономической эффективности инвестиционных проектов компаний, при определении стоимости имущества с учетом временного периода, при вычислении величин инфляции, реального ВВП, в разнообразных финансовых вычислениях исключительное значение имеет правильное вычисление процентных величин и действия с использованием простых и сложных процентов.
Например, если ежемесячно цены растут на 10%, то через год они увеличатся в (1+0,1)12=3,05 раз, т.е. вырастут на (3,05∙100–100)=205%.
Дата добавления: 2015-11-26; просмотров: 810;
