Свойства работы как формы обмена энергией

Рассмотрим процесс подвода теплоты от какого-либо источника теплоты к некоторому газу, находящемуся под давлением р и заключенному в оболочку, способную деформироваться без сопротивления. Как известно, тела при нагревании расширяются. При бесконечно малом расширении газа оболочка (контрольная поверхность) системы смещается в сторону окружающей среды на бесконечно малое расстояние dx, которое может быть различным на разных участках поверхности (рис. 2.2).

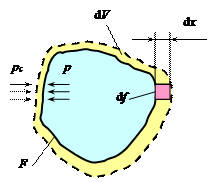Рис. 2.2. Схема объемной деформации

При этом на каждом участке с элементарной площадью df поверхности F бесконечно малая сила рdf совершает над окружающей средой бесконечно малую работу р×df×dx. Для вычисления элементарной работы расширения dL, совершаемой всей термодинамической системой, необходимо просуммировать работу на каждом элементарном участке поверхности F, то есть необходимо вычислить интеграл по всей поверхности F: .

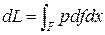Давление р можно вынести за знак интеграла, так как давление газообразных и жидких тел не зависит от ориентации площадки (закон Паскаля). Оставшийся интеграл представляет собой бесконечно малое приращение dV объема всей системы в результате деформации.

Следовательно, элементарная работа расширения физически однородной системы равна:

dL = pdV.

Разделив полученное выражение на массу m однородного рабочего тела, заключенного в объеме V, получим выражение для элементарной удельной работы расширения:

dl = pdu.

В конечном термодинамическом процессе давление в общем случае не остается постоянным, поэтому для вычисления работы процесса требуется интегрирование выражения для элементарной работы по всему процессу от начального состояния 1 до конечногосостояния 2:

.

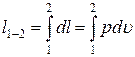Для вычисления интеграла необходимо знать зависимость давления в системе от ее объема в данном термодинамическом процессе р = р(u), которую также можно представить графически на рu-диаграмме (рис. 2.3). Площадь заштрихованной фигуры определяется произведением pdu и поэтому представляет собой элементарную работу расширения dl на элементарном участке процесса, а вся площадь под кривой 1-2 – полную работу процесса.

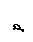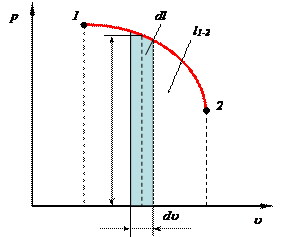Рис. 2.3. Графическое определение работы

Знак элементарной работы dl определяется знаком du, так как абсолютное давление есть всегда величина постоянная. При расширении системы du > 0 (процесс 1-2), работа производится системой над окружающей средой и считается положительной. При сжатии системы du < 0 (процесс 2-1), работа совершается окружающей средой над системой и считается отрицательной. Важнейшим свойством работы как формы обмена энергией является зависимость количества работы от вида термодинамического процесса.

Для термодеформационных систем, обладающих двумя термодинамическими степенями свободы, вид уравнения процесса определяется не только деформационным воздействием, но и одновременно протекающим термическим воздействием, то есть теплообменом. Это выражается зависимостью давления от двух переменных – объема и, например, температуры, а действительная линия такого процесса представляет собой пространственную кривую в координатах р, u, Т.

Поэтому, одно и то же конечное состояние системы может быть достигнуто в ходе различных термодинамических процессов, изображающихся различными пространственными линиями на поверхности состояний F(р, u, Т) = 0.

Проекции этих линий на плоскость рu – диаграммы различны (рис. 2.4), различны и уравнения процессов. В связи с этим различные термодинамические процессы при одинаковых начальном и конечном состояниях дают различные количества работы, которыми система в этих процессах обменивается с окружающей средой.

Рис. 2.4. Зависимость работы от вида термодинамического процесса

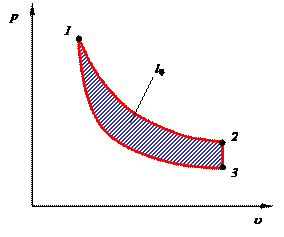Рис. 2.5. Работа термодинамического цикла

Так, например, работа процесса А больше работы процесса В и тем более больше работы процесса С.

Таким образом, работа термодинамического процесса не может быть вычислена по начальному и конечному состояниям системы, она зависит от вида термодинамического процесса, в результате которого система переходит из начального состояния в конечное.

Зависимость работы от вида процесса приводит к ряду важных математических и физических следствий:

1. Элементарная работа не является полным дифференциалом некоторой функции, и интеграл по замкнутому контуру подинтегрального выражения в общем случае не равен нулю.

2. В замкнутом термодинамическом процессе (цикле) 1-2-3-1 (рис. 2.5) система получает от окружающей среды (или отдает ей) некоторое конечное количество энергии в форме работы цикла l_ц, причем в состоянии системы никаких изменений не остается:

.

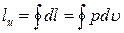Графически указанная работа выражается площадью ограниченной замкнутой кривой 1-2-3-1, полученной алгебраическим суммированием положительных (при du > 0) и отрицательных (при du < 0) площадей, соответствующих процессам расширения и сжатия.

Кроме того, выражение dL = pdV, в котором абсолютное давление р представляет собой потенциал деформационного взаимодействия, а объем V – координату деформационного состояния, позволяет сделать следующее обобщение.

Для всех родов взаимодействия, сопровождающихся передачей энергии любого вида, количество воздействия выражается произведением потенциала данного взаимодействия на изменение соответствующей координаты термодинамического состояния:

dQ_k = P_kdx_k,

где P_k – потенциал взаимодействия k-го рода;

dx_k – координата термодинамического состояния при взаимодействии k-го рода.