Расчет толщины, напряженности внутреннего поля и плотности электрического заряда равновесного p-n-перехода

Данная проблема может быть решена путем нахождения распределения электростатического потенциала в области перехода. На основании уравнений Максвелла

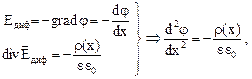(13)

где 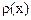– плотность электрического заряда; 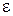– относительная диэлектрическая проницаемость полупроводника; 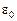– электрическая постоянная.

Уравнение (13) решается для области перехода ( ) при следующих граничных условиях.

1. Напряженность внутреннего диффузионного поля вне перехода равна нулю, т.е.

(14)

2. На металлургической границе перехода потенциал должен быть непрерывным

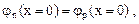(15)

а разность потенциалов 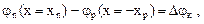(16)

причем величина 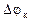определяемой формулой (11).

Интегрируем уравнение (13)

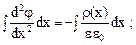(17)

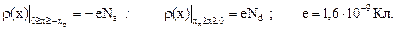(18)

В результате интегрирования получаем

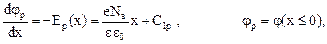(19)

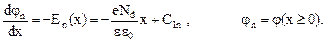(20)

Для определения постоянных 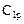и 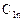используем условие (14)

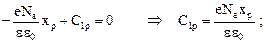(21)

(22)

В результате получаем выражения для напряженности внутреннего поля перехода соответственно со стороны p- и n- областей

(23)

(24)

На рис. 3 изображен график 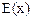внутри перехода.

На металлургической границе (при ) напряженность внутреннего диффузионного поля принимает максимальное значение:

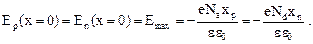(25)

Отсюда имеем

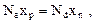(26)

что является условием электрической нейтральности p-n-перехода.

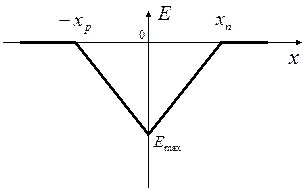
Рис. 3

Для определения толщины обедненного слоя p-n-перехода найдем выражение для электростатического потенциала. Для этого равенства (23) и (24) запишем в виде

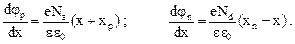(27)

Интегрируя данные уравнения, получаем

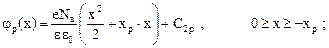(28)

(29)

Из граничных условий (15) следует, что 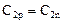, т.е. потенциал определен с точностью до произвольной постоянной. Не нарушая общности результата, можно положить эту постоянную равной нулю.

Выражения (28), (29) и позволяют вычислить толщину d перехода. Действительно, контактная разность потенциалов

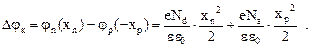(30)

Уравнение (30) совместно с уравнением (26) позволяет определить и .

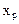(31)

В соответствии с равенством (26) плотность заряда, отнесенного к единичной площади, по обе стороны от сечения

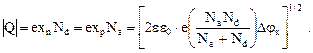(32)

Выражения (11), (25), (31) и (32) и образуют математическую модель резкого p-n-перехода, находящегося в термодинамическом равновесии.