Оценка качества цифровых АС.

Анализ ЦАС как обычно сведем к оценке их устойчивости и качества, то есть к получению и анализу динамических характеристик ЦАС. Обычно ЦАС задана в виде своей Z -передаточной функции Ф(z) X(z)=F(z)×U(z)

и, следовательно, выходной сигнал ЦАС также задан своим изображе-

нием X(z).Возникает вопрос о нахождении оригинала функции x[k] по ее изображению X(Z).

12.1.Обратное Z-преобразование.

Рассмотрим возможные способы нахождения обратного z-преобразования в зависимости от вида изображения x(z).

1.Изображение X(z) задано в виде степенного ряда относительно переменной z^-1

X(Z)=x₀+x₁z^-1+x₂z^-2+...

Тогда, в соответствие с определением прямого z-преобразования, решетчатая функция x[k] имеет вид

x[k]=[x₀,x₁,x₂,...]

Пример: x(z)=z^-1+2z^-3 x[k]=[0,1,0,2,0...]

2.Изображение x(z) задано в общем виде

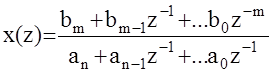
Приравняем данную дробь бесконечному степенному ряду относительноz^-1

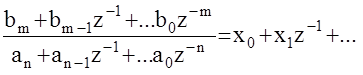
Приведя данное уравнение к общему знаменателю, из условия равенства двух многочленов можно определить неизвестные параметры искомой решетчатой функции x[k]

Пример: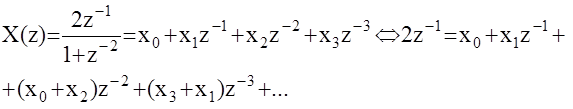

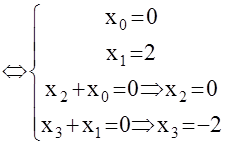x[k]=[0,2,0,-2,...]

3.Недостатком предыдущего метода является то, что для определения любого члена решетчатой функции необходимо знать значения всех предыдущих членов, что не всегда удобно.

Рассмотрим метод, представляющий собой обобщение 2-й теоремы Хэвисайда (разложения) для дискретных систем и исключающий данный недостаток.

Пусть , m£n и корни Z_i полинома

a_n+...+a₀z^-n простые (не кратные)

тогда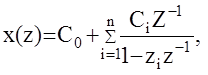

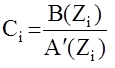
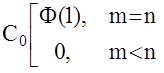
Если ½z_iz^-1½< 1 то каждое слогаемое под знаком å можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с общим знаменателем z_iz^-1, дополняющую на C_iZ^-1,то есть

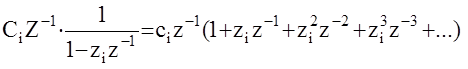
Тогда можно записать

Приравниваем полученное выражение ряду относительно Z^-1

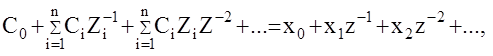
откуда получаем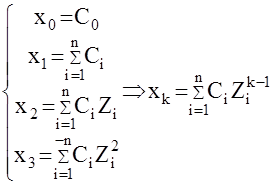

Пример: Вычислить x₆ решетчатой функции x[k] по изображению

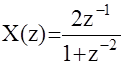m = 1 n = 2 домножим на z² (для удобства)

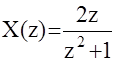z₁=+j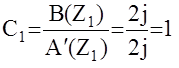

z₂=-j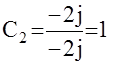

Тогда :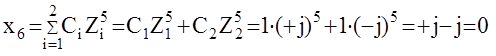

То есть не потребовалось определять предыдущих значений решетчатой функции.

12.2.Временные характеристики ЦАС.

По аналогии с непрерывными АС к временным характеристикам ЦАС будем относить весовую и переходную решетчатые функции - реакции на решетчатые единичные импульсную d[k] и ступенчатую 1[k] функции соответственно при нулевых начальных условиях.

Весовая функция : g[k]=[g₀,g₁,g₂,...], G(z)=g₀+g₁z^-1+...

Определение: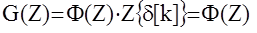

Следовательно Ф(Z)=g₀+g₁z^-1+g₂z^-2+..., и по известной g[k] можно всегда определить z- передаточную функцию системы.

С другой стороны если известна весовая функция системы g[k] и входная решетчатая функция y[k], то

X(Z)=F(Z)×Y(Z)=G(Z)×Y(Z)=(g₀+g₁z^-1+g₂z^-2+...)(y₀+y₁z^-1+y₂z^-2+...)

или (x₀+x₁z^-1+x₂z^-2+...)=g₀y₀+(g₀y₁+g₁y₀)z^-1+(g₀y₂+g₁y₁+g₂y₀+...)z^-1

Получаем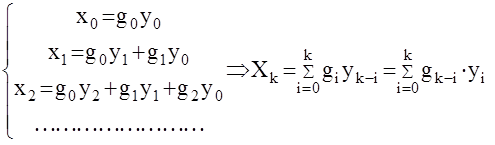

Данная формула является дискретным аналогом интеграла Дюамеля для ЦАС и позволяет определить выходную решетчатую функцию x[k] по известному входу и весовой функции.

Пример :F(z)=z^-1, y[k]=1[k] , x₁₀=?

G(z)=F(z)=z^-1Þg[k]=[0,1,0,0,...]

тогда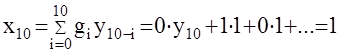

Переходная функция: h[k]=[h₀,h₁,h₂,...], H(z)=h₀+h₁z^-1+...

h[k]- это реакция на единичную решетчатую функцию 1[k], поэтому используя дискретный аналог интеграла Дюамеля имеем

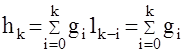
Получили известное соотношение, что переходная решетчатая функция есть сумма весовой и наоборот первая разность от переходной функции есть весовая функция

Ñh[k] = g[k]

12.3.Псевдочастотные характеристики цидоровых АС.

Пусть W(Z) - z -передаточная функция цидоровой АС. Напомним, что 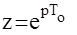и переход к частотным характеристикам осуществляется заменой переменной Лапласа р на комплексную переменную jw, то есть АФЧХ ЦАС имеет вид .

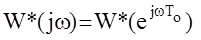Очевидно, что использование такого экспоненциального аргумента неудобно. Возникает вопрос, как обойти эту трудность?

Вновь рассмотрим v-преобразование 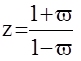или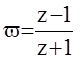

То есть от передаточной функции W(Z) в пространстве Z мы перешли к передаточной функции W(v) в пространстве v. Попробуем определить частотные характеристики в новом пространстве.

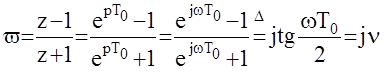где 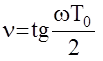-называется

относительной псевдочастотной пространства v, а соответствующие характеристики W(jn)- псевдочастотными характеристиками ЦАС.

В диапазоне низких частот . Чтобы избавиться от зависимости относительной псевдочастоты n от периода квантования Т₀, вводится понятие абсолютной псевдочастоты.

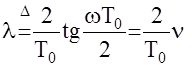и в области низких частот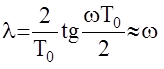

абсолютная псевдочастота l совпадает с истинной частотой w, следовательно и соответствующие частотные характеристики непрерывных W(jw) и цифровых W*(jl) АС в этой области совпадают. Область низких частот определяется условием

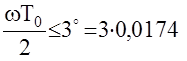рад

Пример: Для БЦВМ ,,Орбита-20’’ тактовая частота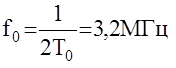

Тогда возможный диапазон частотных характеристик

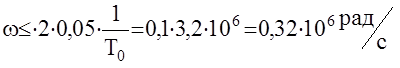
То есть охватывается весь возможный диапазон авиационных АС!!!

12.4.Выбор периода квантования цифровых АС.

Очевидно задача анализа и синтеза ЦАС может быть решена если известен период квантования Т₀ системы. Отсюда возникает естественный вопрос : каким образом задавать величину Т₀. Этот вопрос является исключительно важным, особенно для систем управления летательными аппаратами, так как парамерт Т₀ в основном определяет требования к быстродействию БЦВМ.

Один из важных подходов к решению этой задачи может быть предложен на основе рассмотренного выше перехода к псевдочастотным характеристикам. Условие эквивалентности частотных характеристик непрерывной и цифровой АС имеет вид

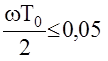
Если в качестве частоты w задать верхнюю границу полосы пропускания исследуемой или синтезируемой АС w_P то тогда

Пример: Математическая модель короткопериодического движения маневренного самолета в боковом канале

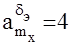
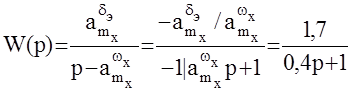
Полоса пропускания апериодического звена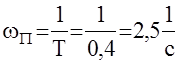

Тогда период квантования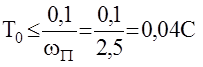

Таким образом, Т₀ следует выбирать из этого условия. При этом в пределах полосы пропускания АС для анализа ЦАС можно пользоваться характеристиками непрерывных систем.

Более общий подход к выбору величины Т₀ основывается на выполнении условий теоремы Котельникова (Шенкона). Данная теорема определяет необходимые условия точного восстановления исходного непрерывного сигнала по его решетчатой функции.

Теорема: Для того, чтобы непрерывный сигнал x(t), разложение которого в ряд Фурье имеет ограниченный спектр (w£ w_max ) , можно было точно восстановить по его решетчатой функции x[kT₀], необходимо, чтобы частота квантования w₀=2pf₀=1/T₀ удовлетворяла условию w₀>2w_max или T₀< 1/2×w_max

Пример: Пусть x(t)=2sint; w_max=1¹/c, тогда Т₀<1/2, возьмем Т₀=с p/2

тогда x[k]=[2sinkT₀]=[0,2×sinp/2,2sinp,...

Возьмем Т₀=p[c] x[k]=[2sinkT₀]=[0,0,0,...] k=0, k<1

12.5.Анализ качества ЦАС.

Анализ качества ЦАС будем проводить на примере следящих систем с ЦВМ в контуре управления. Для таких систем основополагающими понятиями качества являются: астатизм системы и ошибки в установившемся режиме.

Вспомним, что следящая АС называется астатической 1-го порядка, если она безошибочно отслеживает постоянный входной сигнал, математически это означает h[¥]=1

Воспользуемся предельной теоремой:

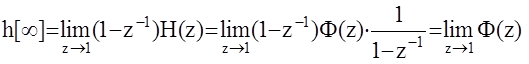
Таким образом, условие астатизма 1-го порядка следящей ЦАС

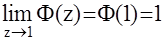
Ошибка в установившемся режиме очевидно равна E[¥]=1-h[¥]

С помощью переходной решетчатой функции можно оценить прямые показатели качества : перерегулирование, время регулирования, время срабатывания. Методика такой оценки будет подробно рассмотрена на практическом занятии.