Устойчивость ЦАС. Необходимые и достаточные условия ус­тойчивости.

Рассмотрим цифровую АС, динамика которой записывается раз­ностным уравнением

a_nx[k]+a_n-1x[k-1]+...+a₀x[k-n]=b_my[k]+b₀y[k-m]

Как и в случае непрерывных систем, устойчивость определяется только свободным (невозмущенным) движением системы, то есть од­нородным разностным уравнением вида:

a_nx_св[k]+a_n-1x_св[k-1]+...+a₀x_св[k-n]=0

Общее решение данного уравнения имеет вид

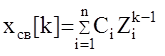где C_i-некоторые произвольные константы,

Z_i-корни характеристического полинома системы

a_n+a_n-1z^-1+...+a₀z^-n=0Ûa_nzⁿ+a_n-1z^n-1+...+a₀=0

(отметим, что эквивалентность этих полиномов определяется из усло­вия 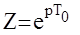то есть z никогда не равняется 0).

Для устойчивой системы свободное движение затухает с тече­нием времени 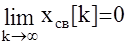, другими словами установившееся значе­ние решетчатой функции х_св[¥] равняется нулю.Исходя из этого сформулируем необходимые и достаточные условия устойчивости в виде следующей теоремы.

Теорема: Для того, чтобы цифровая АС была устойчивой необхо­димо и достаточно, чтобы модули всех корней Z_i ее характери­стического A(z)=0 были меньше единицы ½z_i½< 1

Доказательство: Рассмотрим предельное соотношение для k-того члена x[k]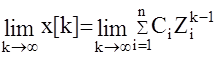

Так как коэффициенты характеристического полинома A(z)=0 дейст­вительны, это значит, что все корни Z_i либо действительные либо комплексно сопряженные:

а)допустим все Z_i действительные, Z_i=a_i,

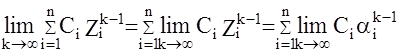Данное выражение равно нулю, когда все a_i по модулю меньше 1, то есть

"_i : ½a_i ½=½Z_i ½< 1

б) допустим есть комплексно-сопряженные корни

Z_i=a_i+jw_i

тогда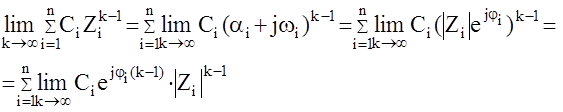

Последнее выражение стремится к нулю лишь при условии ½Z_i½<1

что и требовалось доказать.

Геометрически это интерпретируется так:

Однако использование такого критерия предполагает нахождение корней Z_i характеристического полинома системы, что при больших n достаточно трудно.Применение же других критериев Гурвица, Михай­лова,... связано с оценкой расположения корней в левой части ком­плексной плоскости,а не внутри круга единичного радиуса. Возникает вопрос как использовать данные критерии для цифровых систем?

11.2.Билинейное преобразование характеристического уравнения

цифровой АС.

Введем в рассмотрение некоторое билинейное w-преобразование (дубль вэ)

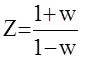В этом случае характеристическое уравнение сис­темы A(Z)=0, преобразуется

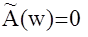Рассмотрим как в этом случае видоизменяется условие ус­тойчивости ½Z½<1.

Допустим w= a+jb , тогда

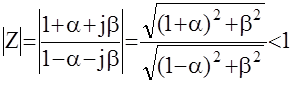Подкоренные выражения всегда по­ложительны, поэтому последнее неравенство можно переписать в виде (1+a)²+b²<(1-a)²+b² или 1+2a+a²+b²<1-2a+a²+b²ÛLa<0

или a<0 Таким образом, w -преобразование позволяет условие ус­тойчивости ½Z½<1 в комплексной плоскости Z перевести в условие Re w = a<0 комплексной плоскости w , и следовательно применять в пространстве w известные критерии устойчивости.

Пример: A(z)=z²-z+1 подставим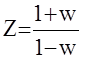

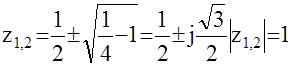
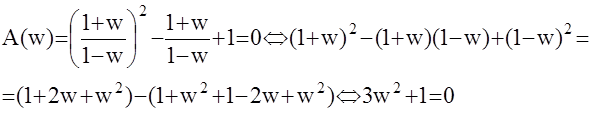
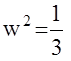
Система на границе устойчивости. Матрица Гурвица:

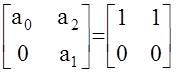D₁=1 > 0 D₂=0½Þсистема на границе устойчиво­сти.

11.3. Представление цифровых АС в пространстве состояний.

При построении систем управления современными летательными аппаратами широко используются методы, основанные на векторно-матричном описании процессов управления. Для непрерывных систем эти методы достаточно подробно рассматривались в разделе ,, Много-

мерные автоматические системы’’. Попробуем распространить эти подходы для описания цифровых автоматических систем.

Уравнение состояния многомерной АС

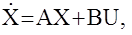при X(0)=X₀

имеет своим решением (формула Коши)

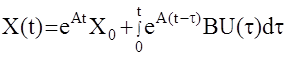
Перейдем в этом уравнении к дискретному времени t=kT₀, и интеграл возьмем методом прямоугольников (левых) k=0,1,2,...

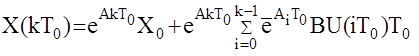
обозначим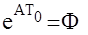

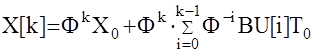
k = 0 X[0]=X₀ D=ФBT₀

k = 1 X[1]=Ф×X₀+ФBU[0]T₀=Ф×X[0]+D×U[0]

k = 2 X[2]=Ф²X₀+Ф²(BU[0]T₀+Ф^-1BU[1]T₀)=

=Ф²X₀+Ф²BU[0]T₀+ФBU[1]T₀=

=Ф[ФX₀+ФBU[0]T₀]+FBT₀U[1]

Или окончательно уравнение состояния цифровой АС

X[k]=FX[k-1]+DU[k-1]

где X[k]- решетчатая вектор-функция состояния n´1;

U[k]- решетчатая вектор-функция входа m´1;

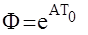- дискретный аналог матричной экспоненты-матрицы состояния цифровой АС n´n;

D=F×B×T₀- матрица эффективности управления ЦАС n´m

На практике матрица Ф может вычисляться по формуле Эйлера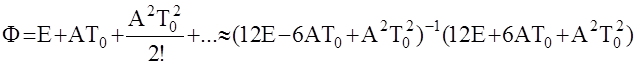

Применим к уравнению состояния ЦАС дискретное преобразование Лапласа

X(z)=F×z^-1 X(z)+Dz^-1U(z)ÛzX(z)-Fx(z)=DU(z) z-скаляр

x(z)=(E×z-F)^-1DU(z)

Матричная передаточная функция n´m . Анализ ЦАС по передаточной функции может вестись по рассмотренным ранее мотодикам.

11.4.Устойчивость многомерных ЦАС.

Матричная z -передаточная функция многомерной ЦАС

W(z)=(Ez-F)^-1D

имеет своим характеристическим полиномом

det(Ez-F)

Очевидно, что необходимое и достаточное условие устойчивости имеет вид ïZ_iï<1, i=1,2,...,n где Z_i - корни характеристического полинома или собственное значение матрицы состояния Ф.

Попробуем вновь обойти проблему нахождения этих собственных значений, путем применения второго метода Ляпунова.

Рассмотрим свободное движение ЦАС

X[k]=FX[k-1]

и построим для нее положительно определенную квадратичную форму

V[k]=X^T[k]GX[k]

Применим оператор первой разности к данной форме с учетом уравнения состояния ЦАС

ÑV[k]=V[k]-V[k-1]=x^T[k]Gx[k]-x^T[k-1]GX[k-1]=

=X^T[k-1]F^TGFX[k-1]-x^T[k-1]GX[k-1]=

=X^T[k-1](F^TGF-G)X[k-1]

Потребуем, чтобы Ф^ТГФ-Г=-b, где b- положительно определенная матрица, тогда ÑV[k]=-X^T[k-1]bX[k-1]

И так имеем положительно-определенную функцию V первая разность от которой есть функция отрицательно-определенная. При этих условиях можно сформулировать аналог второго метода Ляпунова для линейных многомерных ЦАС.

Теорема: Для того, чтобы линейная многомерная ЦАС была устойчи-

вой X[k]=FX[k-1]+DU[k-1] необходимо и достаточно,

чтобы матричное уравнение Ф^ТГФ-Г=-b

( b - заданная положительно определенная матрица) имело

своим решением положительно определенную матрицу Г.

Данное уравнение называется аналогом уравнения Ляпунова для ЦАС.