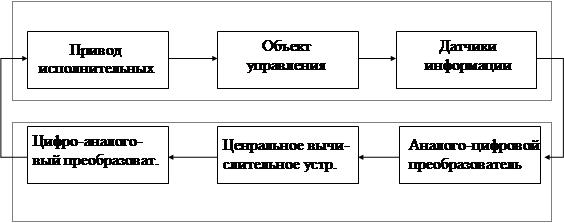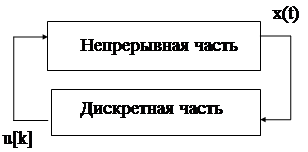Основные свойства цифровых АС.

10.1. Структура цифровых систем управления.

В современной технике, в том числе и авиационной, наряду с не­прерывными широко применяются дискретные автоматические сис­темы, в которых вся информация или ее часть представляется в виде дискретных (прерывистых) сигналов. Дискретные системы, в которых информация циркулирует в виде последовательности импульсов назы­ваются импульсивными. Если в виде последовательности кодов -циф­ровыми. В дальнейшем будем рассматривать цифровые автоматиче­ские системы (ЦАС). Такие системы обладают рядом преимуществ по сравнению с непрерывными.

1.Удобство хранения и обработки дискретной информации в бор­товых цифровых вычислительных машинах (БЦВМ) и системах (БЦВС).

2.Возможность многоканальной (мультиплексной) связи и управ­ления. Когда по одному проводу (каналу) можно передавать несколько управляющих сигналов, разделенных во времени.

3.Структургая гибкость и унифицированность цифровых систем, определяемая заменой программ БЦВМ(принцип программного управления).

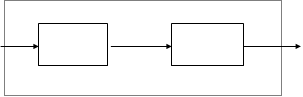
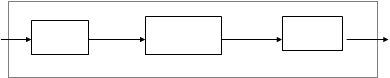
Однако, с другой стороны, включение БЦВМ в замкнутые кон­туры стабилизации короткопериодических (быстрых) движений ЛА, часто приводит к возникновению в таких системах нежелательных по­бочных эффектов, связанных с динамическими особенностями БЦВМ, как звена системы автоматического управления. Кроме того, ЦАС ха­рактеризуется квантованием сигналов, запаздыванием, обусловленным конечным быстродействием БЦВМ, ошибками дискретизации сигна­лов. То есть можно сказать, что ЦАС представляют собой специаль­ный класс автоматических систем и их изучение составляет один из важнейших разделов современной теории автоматического управле­ния. Обобщенная функциональная схема цифровой АС имеет вид

Бортовая ЦВМ, используемая для управления, осуществляет пре­образования входных сигналов x(t) в выходные u(t) в соответствии с заложенными в ней алгоритмами и программами. На вход БЦВМ в общем случае поступает весьма разнообразная информация, одна часть которой представляется дискретным способом (в виде кодов), а другая часть - аналогичным способом (в виде токов, напряжений, уг­лов поворота и т.д.). Поэтому БЦВМ содержит устройства обеспечивающие преобразование аналоговых входных сигналов в цифровой код машины (АЦП) и наоборот (ЦАП).

10.2.Виды квантования информации в цифровых системах.

Прооцесс преобразования непрерывной функции х(t) в цифровой код машины можно условно разделить на три этапа:

1) квантование по времени; 2)квантование по уравню; 3)кодирование.

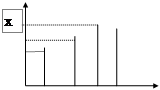
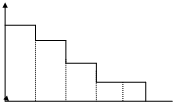
Кавнтование по времени соответствует фиксации мгновенных значений непрерывно изменяющейся функции х(t) в дискретные моменты времени kT₀(k=0,1,2,...-дискретное время,Т₀-период квантования) и установления некоторого соответствия между этими значениями и параметрами последовательности импульсов (обычно прямоугольных). Такой процесс еще называется импульсной модуляцией.

Модулирующая функция немодулированная последователь-

х(t) ность импульсов.

Основными параметрами немодулированной последовательности импульсов являются:

-высота или амплитуда импульса А;

-длительность или ширина импульса t=jT₀ 0(<j£1-скважность импульса)

-период квантования или расстояние между импульсами Т₀.

В соответствии с тем какой из параметров импульсов варьируется различают:

-амплитудно-импульсную модуляцию:

A=Var, T₀=Const,t=Const

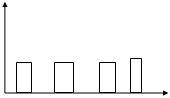
-широтно-импульсивная модуляция:

A=Const, T₀=Const,t=Var

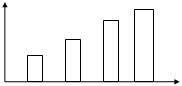
-время- импульсная модуляция:

A=Const, T₀=Var, t=Const

В дальнейшем будем рассматривать только амплитудно-импульсную модуляцию: то есть высота импульса пропорциональна текущему значению непрерывного сигнала, длительность и период квантования постоянны. Если длительность импульсов t=jT₀ существенно меньше периода квантования (j<<1), а непрерывная часть системы состоит из звеньев с постоянными времени Т_i>>jT₀, но последовательность импульсов можно рассматривать как дискретный сигнал x[kT₀], со значениями равными мгновенными значениями амплитуд х(t), t=kT₀. Такое идеализированное (t®0) представление дискретного сигнала называется решетчатой функцией.

Очевидно, эта функция определена только в дискретные моменты времени 0,Т₀,2Т,3Т₀,... и будет в дальнейшем обозначаться x[k], k=0,1,2,...

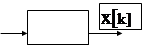
Преобразование непрерывного сигнала в решетчатую функцию осуществляется идеальным импульсным элементом, который обозначается так:

Приведем примеры некоторых решетчатых функций

а)единичная ступенчатая решетчатая функция

1[k]=[1,1,1,....]

б)единичная импульсная решетчатая функция

б[k]=[1,0,0,...]

в)линейно нарастающая решетчатая функция

[kT₀]=[0,T₀,2T₀,...] [k]=[0,1,2,...]

г)экспотенциальная решетчатая функция

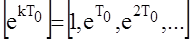
В цифровых системах после рассмотренного выше квантования сигнала по времени осуществляется квантование по уровню, которое состоит в замене в соответствующие моменты времени мгновенных значений непрерывной величины x(t), t₂, kT₀ (элементов ее решетчатой функции) x[k] ближайшими разрешенными значениями x[k]. Эти значения определяются принятой системой счисления и длиной разрядной сетки БЦВМ. Так для двойной системы счисления и пятиразрядной сетке имеем

x[1]=-0,18₁₀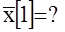

а) Переводим в двоичную систему

0,18´2=0,36´2=0,72´2=1,44´2=0,88

б) Заполняем разрядную сетку

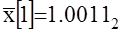
Если перевести обратно в десятичную систему, то

1.0011₂=0×2^-1+0×2^-2+1×2^-3+1×2^-4=0,125+0,0625=0,1875₁₀

Ошибка округления (квантования по уравню) составляет 0,0075₁₀ и очевидно максимальное ее значение £0,5h, где h- ,,вес’’наименьшего разряда. Графически процесс квантования по уровню можно представить так

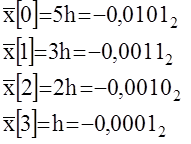
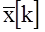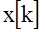Очевидно близость решетчатых функций и зависит от длины разрядной сетки БЦВМ(то есть от величины h). Чем больше количество разрядов (меньше значение h)м меньше период квантования Т₀, тем точнее 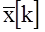воспроизводит исходную непрерывную функцию х(t).

Кодирование состоит в преобразовании сигнала 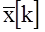в цифровой код

БЦВМ 10011-прямой код;

11100-обратный(инверсия мантиссы прямой для отрицательных чисел);11101-дополнительный(+1 к младшему разряду обратного).

например :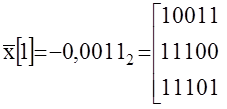

Таким образом, выходным сигналом АЦП является дозированный сигнал 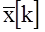, который поступает в процессор БЦВМ где по определенному алгоритму осуществляется его обработка. Выходной сигнал в итоге также кодированный, поэтому в дальнейшем необходимо его декодирование и экстраполяция.

Декодирование заключается в преобразовании цифрового кода БЦВМ 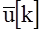в элементы решетчатой функции 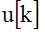, той размерности и величины, которые в дальнейшем используются в непрерывной части АС.

Экстрополяция или интерполяция заключается в формировании непрерывной функции u(t) из решетчатой u[k]. Вообще говоря одной решетчатой функции соответствует бесконечное множество непрерывной, но в авиационной практике обычно экстрополяция представляет собой фиксацию выходного сигнала БЦВМ на постоянном уравне в течение периода квантования Т₀.

Декорирование и экстрополяция осуществляются в цифро-аналоговых преобразователях (ЦАП).

10.3.Математическое описание цифровых автоматических систем.

В общем случае любая ЦАС состоит из непрерывной и дискретной частей Динамика непрерывной части ЦАС описывается, как известно, дифференциальными уравнениями. Для них разработан специальный математический аппарат анализа и синтеза, основанный на преобразовании Лапласа. Динамика дискретной части описывается уже разностными уравнениями, являющимися аналогами дифференциальных. В них в качестве аналоглв производных и интегралов присутствуют разности и суммы решетчатых функций входных и выходных сигналов.

Возникает проблема: как исследовать такие системы в целом? То есть необходимо определить пути перехода либо к эквивалентной неперывной системе либо к эквивалентной дискретной. Но для начала напомним основные положения теории разностных уравнений и дискретного преобразования Лапласа.

Выражение Dх[k]=x[k+1]-x[k] - называется прямой разностью первого порядка решетчатой функции x[k] в момент времени t=kT₀.

Выражение Ñx[k]=x[k]-x[k-1] - назывется обратной разностью первого порядка решетчатой функции x[k] в момент времени t=kT₀.

Прямая разность предполагает знание будущего значения решетчатой функции, что не всегда возможно. Поэтому в дальнейшем под общим термином разность будем понимать обратную разность.

Очевидно, что Ñ можно рассматривать как оператор первой разности. Если применить этот оператор ко всем элементам решетчатой функции, то получим новую решетчатую функцию, каждый элемент которой есть первая разность для соответствующих моментов времени

Ñx[k]=z[k]-x[k-1], k=0,1,2,...

Для удобства в дальнейшем Ñx[k] будет означать решетчатую функцию первой разности

Ñ{1[k]}=Ñ{1,1,...1}={1[0]-1[-1],1[1]-1[0],...}=[1,0,0,...]=d[k]

Выражение Ѳx[k]=Ñx[k]-Ñx[k-1]=x[k]-x[k-1]-x[k-1]+x[k-2]

называется второй разностью для момента времени kT₀.

Разность n-го порядка определяется так:

,

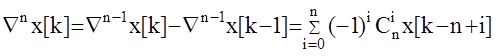где 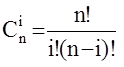- коэффициенты бинома Ньютона.

Можно заключить, что в определенном смысле разности являются аналогами производных для непрерывных систем. Однако следует помнить, что только аналогами и выражение

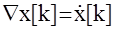
выполняется только в исключительных случаях, так как производная представляет собой предельное соотношение в отличие от первой разности.

Рассмотрим теперь сумму k+1 элементов решетчатой функции x[k] в момент времени kT₀.

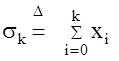
Докажем, что эта сумма является аналогом интеграла для цифровых АС. Применим для этого оператор первой разности к сумме s_k в момент времени kT₀ :

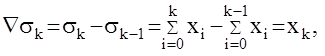
если k изменить от 0 до¥ то получим решетчатую функцию s[k] ,которая является аналогом интеграла для функции x[k]. Оператор суммирования будем обозначать 1/Ñ

Пример: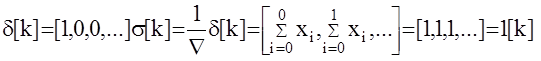

Теперь введем понятие разностного уравнения.

Линейным стационарным разностным уравнением n -го порядка называется уравнение вида

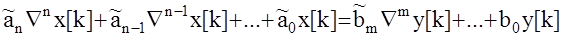
Если раскрыть операторы i разностей и привести подобные при одинаковых решетчатых функциях x[k-i] и y[k-j], то данное уравнение можно записать в следующем виде :

a_nx[k]+a_n-1x[k-1]+...a₀x[k]=b_my[k]+...+b₀y[k-m]

То есть разностные уравнения в отличие от их аналогов от их аналогов дифференциальных представляют собой обычные алгебраические рекуррентные соотношения, позволяющие определить в момент времени kT₀ значение решетчатой функции выходного сигнала x[k] по заданной входной решетчатой функции y[k] .

Поэтому анализу АС в дискретной области более прост и предпочтителен по сравнению с аналоговыми системами.

10.4.Дискретное преобразование Лапласа.

Представим решетчатую функцию x[k] в виде непрерывной функции (последовательности d -импульсов)

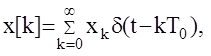где x_k -значение решетчатой функции x[k] в момент времени kT₀ и найдем ее изображение по Лапласу.

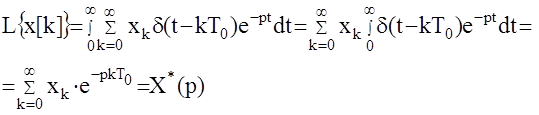
Выражение 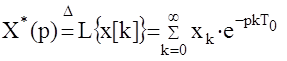называется прямым дискретным преобразованием Лапласа решетчатой функции x[k] или D -преобразованием. Если ввести обозначение 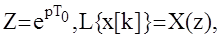то получим 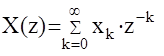Такая операция суммирования получила название Z - преобразование. Она отличается от дискретного преобразования Лапласа только своим аргументом (Z вместо Р ), что удобно в записи. Рассмотрим как связаны комплексные области переменных Р и 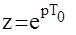Пусть 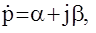тогда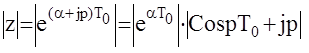

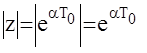
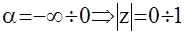
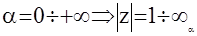
Таким образом, мнимая ось в области р превратилась в окружность 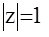в области z . Отметим, что z - преобразование для дискретных систем играет такую же роль, что и обычное преобразование Лапласа для непрерывных систем.

10.5.Z-изображения функций времени.

По определению Z -изображение есть ни что иное как сумма бесконечного степенного ряда 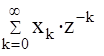.Возникает вопрос о сходимости данного ряда, то есть о существовании конечного аналитического выражения для Z - изображения. Ответ на этот вопрос дает следующая теорема, которую приводим без доказательства.

Теорема: Степенной ряд 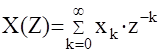сходится абсолютно в каждой точке комплексной плоскости, где выполняется соотношение

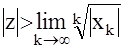
Определим теперь Z -изображения некоторых функций времени.

1.Z -изображение единичной импульсной решетчатой функции

Z{d[k]}=Z{[1,0,0,...]}=1×z⁰+0×z^-1+...=1

2.Z -изображение единичной ступенчатой решетчатой функции

Z{1[k]}=Z{[1,1,1,...]}=1×z⁰+1×z^-1+1:z^-2+...

В соответствии с теоремой данный ряд сходится абсолютно в точках комплексной плоскости удовлетворяющих неравенству

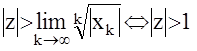
В этом случае Z -изображение представляет собой бесконечно-убывающую геометрическую прогрессию с общим знаменателем z^-1, сумма которой равна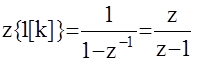

3. Z - изображение экспоненциальной решетчатой функции

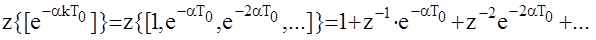
Согласно теореме данный ряд сходится в точках, удовлетворяющих условию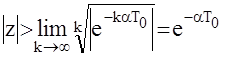

Это вновь бесконечно убывающая геометрическая прогрессия с общим знаменателем 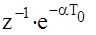и ее сумма равна

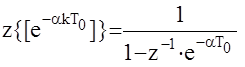
Z - изображения наиболее часто встречающихся функций времени приводятся в соответствующих таблицах.

10.6.Основные свойства Z-преобразования.

1.Свойство линейности:

Z{ax[k]+by[k]}=aZ{x[k]}+bZ{y[k]}

Z^-1{ax[k]+by[k]}=aZ^-1{x[k]}+bZ^-1{y[k]}

2.Z -изображения решетчатых функций, смещенных в сторону опережения и запаздывания.

Запаздывание на один период:Z{x[k-1]}=Z{0,x₀,x₁,...}=

=0×z⁰+x₀z^-1+x₁z^-2+...=z^-1(x₀+x₁z^-1+...)=z^-1X(z)

Или в общем случае (запаздывание на i периодов)

Z{x[k-i]}=Z^-iX(z)

Определим теперь Z -изображение решетчатой функции x[k+1]

Опережение на один период: Z{x[k+1]}=Z{x₁,x₂,...}=x₁+x₂z^-1+...=

=(обавим x₀z-x₀z) x₁+x₂z^-1+...+x₀z-x₀z=z(x₀+x₁z^-1+x₂z^-1+x₂z^-2+...)-

-x₀z=z×X(z)-x₀z

Так как значение х₀ является начальным для решетчатой функции [k+1] , то при нулевом начальном условии Z{x[k+1]}=z×X(z)

или в общем случае, при нулевых начальных условиях x₀=x₁=...x_i-1=0,

Z{x[k+i]}=ZⁱX(z)

3. Z -изображения конечных разностей и сумм.

Определим Z -изображение решетчатой функции первой разности :

z{Ñx[k]}=z{x[k]-x[k-1]}=z{x[k]}-z{x[k-1]}=X(z)-z^-1X(z)=

=(1-z^-1)X(z)

Z -изображение решетчатой функции 2-й разности:

z{Ѳx[k]}=z{Ñx[k]-Ñx[k-1]}=z{x[k]-x[k-1]-x[k-1]+x[k-2]}=

=z{x[k]-2x[k-1]+x[k-2]}=X(z)-2z^-1X(z)+z^-2X(z)=(1-z^-1)²X(z)

Или в общем случае для i -итой разности:

z{Ñⁱx[k]}=(1-z^-1)X(z)

При определении Z -изображения решетчатой функции суммы s[k] воспользуемся известным соотношением

Ñ{s[k]}=x[k]

Применим к этому соотношению оператор Z

z{Ñ{s[k]}}=z{x[k]}Û(1-z^-1)å(z)=X(z)

å(z)=1/1-z^-1×X(z)

4.Начальные и конечные значения решетчатой функции могут быть определены по ее Z -изображению с помощью предельных теорем (аналогичных теорем для непрерывных систем)

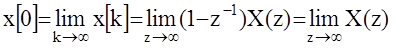
Пример: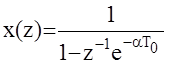

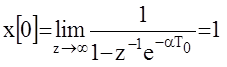
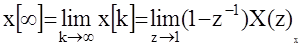
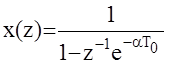
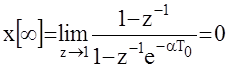
10.7.Передаточная функция ЦАС.

До сих пор рассмотрение ЦАС сводилось к изучению свойств и математического описания дискретных сигналов (решетчатых функций).Теперь попробуем рассмотреть случаи воздействия этих сигналов на чисто дискретные элементы ЦАС (динамика которых описывается разностными уравнениями) и на непрерывные элементы (с дифференциальными уравнениями).Пусть на вход дискретного элемента, описываемого линейным разностным уравнением n -го порядка

a_nx[k]+a_n-1x[k-1]+...+a₀x[k-n]=b_my[k]+...+b₀y[k-m]

действует входной решетчатый сигнал y[k] , выход x[k] . Применим к данному уравнению Z -преобразование при нулевых начальных условиях:a_nX(z)+a_n-1z^-1X(z)+...+a₀z^-nX(z)+b_m-1z^-1I(z)+...+b₀z^-mY(z) или

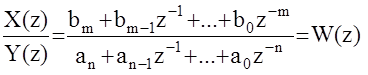m<n-физическая реализуемость

По аналогии с непрерывными системами данное выражение назовем передаточной функцией дискретного элемента и будем называть

Z -передаточная функция.

Определим передаточные функции некоторых дискретных элементов

1)Элемент первой разности :.

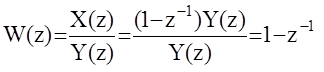
2)Элемент суммы:

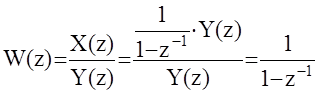Для таких чисто дискретных элементов справедливы формулы структурных преобразований, выведенные для непрерывных систем:

-последовательное соединение W(z)=W₁(z)×W₂(z)

-параллельное соединение W(z)=W₁+W₂(z)

-встечно-параллельные соединения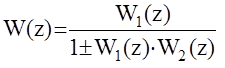

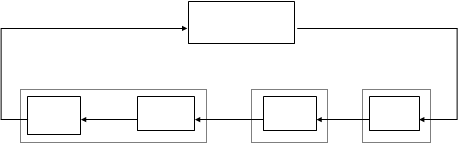
Однако, цифровая АС обычно содержит не только дискретные, но и непрерывные элементы, то есть, как говорят, имеет смешанную ,,р-z’’

структуру

Возникает вопрос, как в этом случае определить Z -передаточную функцию системы? Для того чтобы решить эту задачу необходимо перейти от смешанной ,,р-z’’структурной схемы к схеме, содержащей только z-передаточные функции. При этом необходимо учитывать следующую специфику цифровых систем

То есть эквивалентный переход от ,,р-z’’ структуры к ,,z’’-структуре правомочен лишь в случае приведения исходной системы к виду, когда на вход непрерывных элементов действуют дискретные сигналы,а на вход дискретных либо дискретные либо непрерывные!

Только в этом случае справедливы формулы для определения эквивалентных z -передаточных функций соединений звеньев.

Вновь возвратимся к исходной функциональной схеме ЦАС

и исходя из функционального назначения преобразователей АЦП и ЦАП определим их передаточные функции.

Как уже отмечалось, прохождение информации через АЦП характеризуется тремя этапами: амплитудно-импульсная модуляция, квантование по уровню и кодирование. Причем можно принять, что два последних этапа осуществляются мгновенно, поэтому при определении передаточной функции АЦП ими можно пренебречь, то есть

АЦП- это элемент ЦАС, осуществляющий амплитудно-импульсную модуляцию.

То есть выходной сигнал 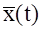представляет собой последовательность прямоугольных импульсов, с амплитудами равными мгновенным значениям входного сигнала x(t) в момент времени kT₀ и длительностью t . Исходя из этого структуру АЦП можно представить как последовательное соединение идеального импульсного элемента, на выходе которого получается решетчатая функция 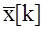и непрерывного формулирующего элемента с передаточной функцией W_ф(р) , на выходе которого получается последовательность импульсов длительностью t , то есть сигнал 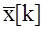. Отметим, что если t=0, то 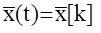иW_ф(р)=1. То есть АЦП в этом случае представляет собой идеальный импульсный элемент. При t¹0, любой импульс в сигнале 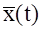можно представить как сумму положительного и отрицательного скачков амплитуды x_i в моменты времени iT₀ и iT₀+t

Тогда в целом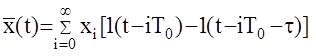

Входной решетчатый сигнал формирующего элемента, можно также представить в виде непрерывной функции

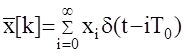
Применим преобразование Лапласа к этим сигналам

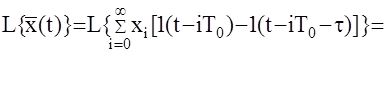
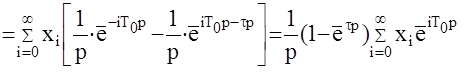Напомним, что t=gT₀, тогда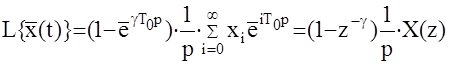

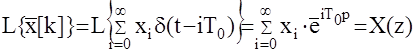
Определим теперь передаточную функцию формирующего элемента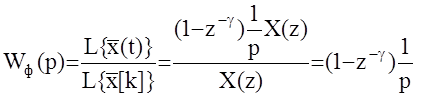

То есть формирующий элемент представляет собой последовательное соединение дискретного и непрерывного элементов, причем именно в этой последовательности, так как вначале определяется новый элемент решетчатой функции х_i ,а затем он ,,запоминается’’ на период t (на интеграторе).

Обычно, для авиационных систем, выходной сигнал ФЦП остается постоянным в течение всего периода квантования Т₀ , то есть g=1

Такие формирующие элементы называются экстраполяторами нулевого порядка или фиксаторами

Как видим на вход непрерывных элементов в АЦП действуют дискретные сигналы, а выход непрерывного элемента подключен к входу дискретного элемента (процессора) БЦВМ, следовательно здесь правомочен переход к Z- передаточной функции АЦП

W_АЦП(z)=W₁(z)×W₂(z)×W₃(z)=W¼

Определим W₃(z), как z - преобразование решетчатой функции, получающейся на выходе звена 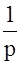, то есть

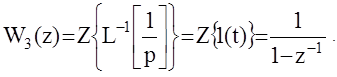Тогда 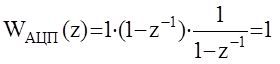То есть при принятых допущениях (квантование по уровню и кодирование осуществляется мгновенно) аналого-цифровое преобразование не оказывает влияние на динамические процессы в ЦАС.

Определим теперь передаточную функцию ЦАП, характеризуемую процессами декодирования и экстраполяции. Если вновь процесс декодирования осуществляется мгновенно и точно, а экстраполяция нулевого порядка, то ,,p-z’’ структура ЦАП имеет вид

Однако выход непрерывного элемента ЦАП и (t) действует на вход непрерывной части всей АС, поэтому переход к Z -передаточной функции ЦАП сразу неправомочен, необходимо предварительное преобразование исходной структуры.

Итак ,,p-z’’структура ЦАС имеет вид: