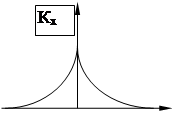Статистическая динамика автоматических систем.

13.1.Определение статистической динамики.

В предыдущих лекциях входные сигналы АС принимались детерминированными, то есть заранее известными функциями времени. Однако на практике это часто не выполняется, и на систему действуют случайные, то есть заранее непредсказуемые сигналы. Например, возможные отказы отдельных элементов системы автоматического управления в полете, шумы различных датчиков информации, порывы ветра, действующие на самолет. Отметим, что такие входные воздействия, изменяющиеся по случайному закону, не могут быть заменены типовыми, стандартными воздействиями в виде заданных функций времени, а переходные процессы в таких системах нельзя рассматривать как следующие друг за другом переходы системы из одного установившегося состояния в другое. Такие системы требуют особого подхода к их исследованию, и они составляют особый класс АС.

Автоматические системы, находящиеся под воздействием случайных входных сигналов, называются стохастическими автоматическими системами.

Раздел автоматики, занимающийся изучением стохастических систем, называется статистической динамикой.

Научной основой ее является теория случайных функций, созданная выдающимися математиками нашего столетия А.Н.Колмогоровым и Н. Винером.В настоящем курсе мы познакомимся лишь с основами статистической динамики, краткие сведения о которых уже получены в курсе ,, Вероятностный анализ кибернетических систем’’

13.2.Случайные процессы и их основные статистические

характеристики.

Случайной функцией одного или нескольких аргументов называется такая функция, значение которой при любых заданных значениях этих аргументов является случайной величиной, то есть величиной, принимающей заранее непредсказуемые значения. В дальнейшем мы будем рассматривать случайные функции одного неслучайного аргумента - времени t.Такие функции называются случайными процессами.

Пример: x(t)- случайный выходной процесс или сигнал.

z(t)-случайная помеха (входной процесс).

В дальнейшем под терминами случайная функция, случайный сигнал, помеха - будем понимать случайные процессы.

Возникает проблемма: каким же образом задать и написать случайную функцию, ведь она принимает в каждый момент времени заранее непредсказуемые значения?

Наиболее очевидный способ - это поставить большое количество экспериментов и зафиксировать конкретный вид случайной функции в каждом эксперименте. Такой конкретный вид случайной функции x(t) в i-том эксперименте называется ее реализацией x_i(t).

То есть случайная функция может задаваться множеством своих реализаций. Однако такое задание очень громоздко и неудобно. Как иначе это сделать? Как известно из курса теории вероятностей существуют определенные закономерности, присущие множеству реализаций случайной функции и эти закономерности описываются уже неслучайными характеристиками. Наиболее полными характеристиками случайных величин и функций являются их функции распределения или плотности распределения вероятностей.

Напомним, что функцией распределения случайной величины x называется функция F(x), равная вероятности события, состоящего в том, что эта случайная величина примет значение меньшее, чем х.

F(x)=P(X<x), где х- определяет область допустимых значений, принимаемых случайной величиной Х.

Производная от функции распределения называется плотностью распределения вероятностей и обозначается

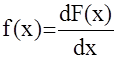Очевидно, что для случайных процессов эти характеристики определены только для отдельных моментов времени (сечений случайной функции) t₁,t₂,t₃,... Для того, чтобы учесть статистическую взаимосвязь различных сечений случайной функции вводится понятие двухмерных, трехмерных и т.д. плотностей распределения.

f₂(x₁,x₂,t₁,t₂), f₃(x₁,x₂,x₃,t₁,t₂,t₃),...

Таким образом, полной характеристикой случайной функции является множество n- мерных (n=1,2,3,...) ее функций или плотностей распределения.

Однако при расчетах не всегда удобно пользоваться этими характеристиками, поэтому обычно применяют так называемые статистические или числовые характеристики случайных процессов, вычисляемые на основе знания только первых двух функций распределения f(x,t) и f₂(x₁,x₂,t₁,t₂), достаточных для описания большинства случайных процессов. К этим статистическим характеристикам относятся: математическое ожидание m_x(t), дисперсия D_x(t), среднеквадратическое отклонение d_x(t) и корреляционная функция K_x(t₁,t₂).

Математическое ожидание (или среднее значение) случайной функции x(t)- это неслучайная функция m_x(t), которая при любом значении аргумента t равна математическому ожиданию соответствующего сечения случайной функции.

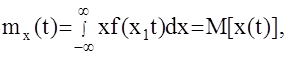
M- символ оператора математического ожидания.

Как видим математическое ожидание, характеризует среднее значение случайной функции. Однако, во многих задачах необходимо оценить разброс значений функции относительно ее математического ожидания. Такая статистическая характеристика называется дисперсией случайной функции x(t) и обозначается D_x(t)

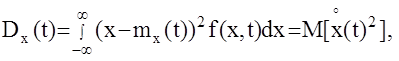
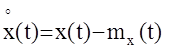-центрированная случайная функция.

Дисперсия случайной функции имеет размерность квадрата этой функции, однако, удобнее пользоваться мерой разброса имеющей ту же размерность, что и случайная величина. За эту меру принимают положительное значение квадратного корня из дисперсии и называют ее среднеквадратическим отклонением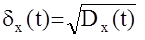

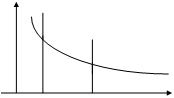
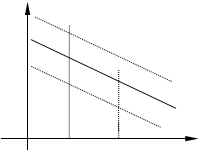
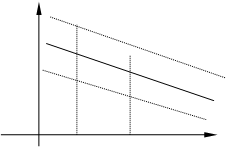
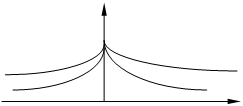
Рассмотрим два случайных процесса x(t) и y(t), имеющих одинаковые математические ожидания m_x(t)=m_y(t) и дисперсии D_x(t)=D_y(t). Но временная структура как видим у них разная.

Характеристикой, определяющей временную структуру случайной функции, то есть связь сечений этой функции в различные моменты времени t₁, t₂, является корреляционная функция.

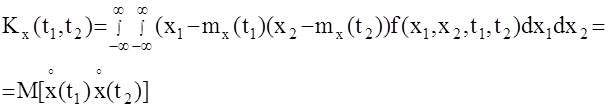
Очевидно, при t₁=t₂=t, x₁=x₂=x

имеем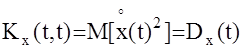

Характеристикой, определяющей статистическую взаимосвязь двух случайных функций x(t) и y(t) используется взаимная корреляционная функция.

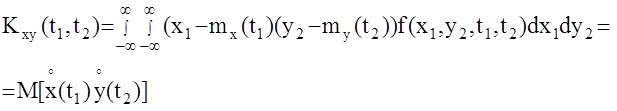
Условие K_xy(t₁,t₂)=0 является условием независимости (некоррелированности) функций x(t) и y(t).

Для некоррелированных случайных функций справедливы следующие соотношения. Если z(t)=x(t)+y(t)

m_z(t)=m_x+m_y(t) ; D_z(t)=D_x(t)+D_y(t) ; ;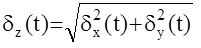

K_z(t₁,t₂)=K_x(t₁,t₂)+K_y(t₁,t₂).

13.3.Статистические характеристики стационарных

случайных процессов.

Существуют случайные функции, не изменяющие свои статистические характеристики с течением времени. Такие случайные функции называются стационарными.

Случайная функция с постоянным математическим ожиданием и

корреляционной функцией, зависящей только от разности аргу-

ментов, называется стационарной (в широком смысле).

m_x(t)=m_x=const K_x(t₁,t₂)=K_x(t₂-t₁)=K_x(t)

Рассмотрим свойства стационарных случайных функций.

1.Корреляционная функция - есть четная функция от t.

2.Корреляционная функция является убывающей и K_x(¥)=0. Это объясняется тем, что чем больше t, тем слабее связь между сечениями случайной функции.

3.Дисперсия постоянна D_x(t)=K_x(t,t)=K_x(0)=D_x=Const.

4.Корреляционная функция не превосходит дисперсии этого процесса

D×K_x(t)£D_x

5.Отношение 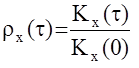называется нормированной корреляционной функцией или коэффициентом корреляции r_х(t) £ 1

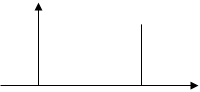
В теории стохастических систем управления большую роль играет один из видов случайных функций, математическое ожидание которого равно нулю, а корреляционная функция пропорциональна d- функции. Такую случайную функцию называют белым шумом z_б.ш.(t)

К_б.ш.(t)=S_б.ш.d(t),

S_б.ш. -постоянная величина, называемая интенсивностью белого шума.

d - функция, при значении аргумента отличном от нуля, равна нулю, поэтому для белого шума случайные величины, соответствующие сколь угодно близким сечениям являются некоррелированными.

Белый шум физически нереализуем, т.к. имеет бесконечную мощность (его дисперсия D_б.ш.=К_б.ш.(0)=¥). Однако такое идеализированное представление случайного процесса является очень удобным в статистической динамике, так как реакция системы на белый шум может быть определена достаточно просто.

13.4.Спектральная плотность стационарных случайных сигналов.

Для анализа характеристик автоматических систем, находящихся под воздействием случайных сигналов, широко применяются частотные характеристики, вычисляемые как прямое преобразование Фурье от рассмотренных выше статистических характеристик. Для стационарных случайных сигналов, от времени зависит только одна характеристика - корреляционная функция, поэтому анализ этих процессов в частотной области осуществляется по одной характеристике - спектральной плотности, представляющей собой прямое преобразование Фурье от корреляционной функции и наоборот.

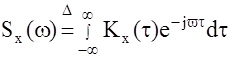
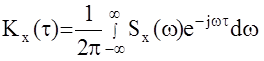
На основании формулы Эйлера e^-jwt=Cosvt-jSinvt можно записать

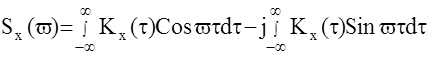
Первое слагаемое есть четная функция, а второе - нечетная и для симметричных пределов интегрирования имеем:

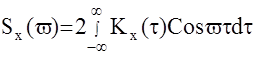
Таким образом, спектральная плотность стационарной случайной функции есть функция действительная и четная.

Свойства спектральной плоскости.

1.Спектральная плоскость неотрицательна на любой частотеv (теорема Винера - Хинчина). Это связано с тем, что мощность любого процесса в любом диапазоне частот не может быть отрицательна.

2.Дисперсия и спектральная плотность связаны соотношением

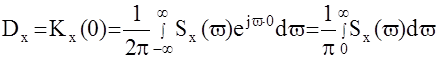
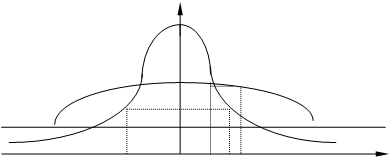
чем положе график S_x(v) тем больше D_x отсюда пункт 3.

3.Установим графическую связь между видом корреляционной функцией и спектральной плоскостью.

Пусть корреляционная функция случайного процесса y(t) связана с корреляционной функцией x(t) соотношением K_y(t)=K_x(at), a>1

Установим при этом связь между спектральными плоскостями процессов x(t) и y(t).

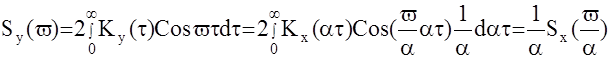
Построим графически,

имея: S_x(v) при a=2

v=0 ; S_y(0)=1/2S_x(0)

v=v₁ S_y(v₁)=1/2S_x(v/2)

То есть чем круче спадает корреляционная функция, тем положе график спектральной плоскости. Другими словами для процессов с медленно спадающей корреляционной функцией большая часть мощности концентрируется в низкочастотном диапазоне. То есть чем меньше статистическая связь между сечениями случайной функции, тем больше гармоник в спектральном представлении случайного сигнала и наоборот. В предельном случае, когда случайный процесс является белым шумом ,

имеем: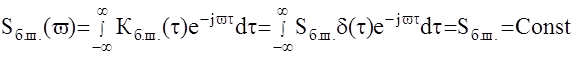

Таким образом, спектральная плотность белого шума постоянна во всем интервале частот, то есть мощность бесконечного числа гармоник в спектральном представлении белого шума постоянна. Это подтверждает невозможность его физической реализации. На практике же считается белым шумом процесс, спектральная плотность которого постоянна в полосе пропускания АС.

13.5. Эргодические случайные процессы и их характеристики.

Чтобы оценить математическое ожидание какой – либо стационарной случайной функции с неизвестной плотностью распределения вероятностей, записать в каждом из них реализации функции, а затем определить в некотором фиксированном сечении среднее значение случайной функции. Очевидно, что при числе реализаций i®¥ это среднее значение будет по вероятности сходиться к математическому ожиданию. Можно сказать, что математическое ожидание является средним по множеству реализаций случайной функции. Существует класс случайных процессов, который позволяет определить статистические характеристики случайного процесса в результате не многих, а одного опыта. В этом случае среднее значение определяется по времени для одной реализации случайной функции.

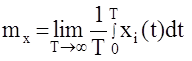
Стационарные случайные процессы, для которых среднее по множеству реализаций равно среднему по времени для одной реализации, называются эргодическими.

Теорема: Для того чтобы, стационарная случайная функция была эрго-

дической достаточно, чтобы ее корреляционная функция стремилась к нулю при неограниченном возрастании t

.

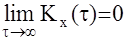Математическое ожидание, корреляционная функция и дисперсия процесса определяются по формулам

; ;

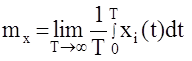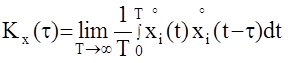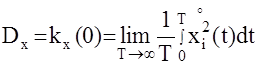При численной обработке реализации случайной функции интегралы в правых частях этих формул заменяются суммами (метод прямоугольников).

; ;

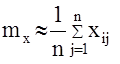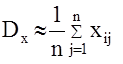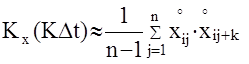
k=1,2,…n; n=T/Dt; Dt- шаг численного интегрирования

x_i-i-тая реализация случайной функции x(t).

13.6. Прохождение стационарного случайного сигнала

через линейную АС.

Одной из важнейших задач статистической динамики является определение статистических характеристик выходного сигнала на основе знания соответствующих характеристик входных сигналов. Рассмотрим решение этой задачи для системы с известной весовой функцией g(t). Как известно, связь между входными и выходными сигналами такой системы дается с помощью интеграла Дюамеля.

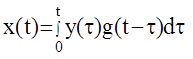
Применим оператор математического ожидания выходного сигнала к правой и левой частям этого уравнения

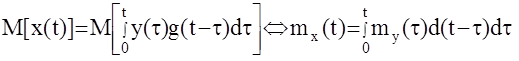
Таким образом, математическое ожидание выходного сигнала есть реакция АС на математическое ожидание входного сигнала. Для стационарного входного сигнала m_y(t)=m_y=Const имеем:

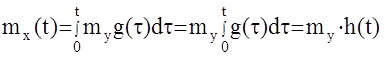, то есть, выходной сигнал АС становится в общем случае нестационарным.

Определим теперь корреляционную функцию выходного сигнала.

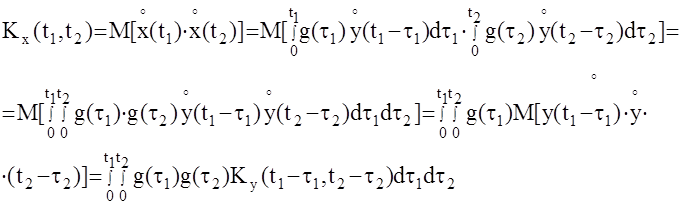Вновь получили, что корреляционная функция выходного сигнала есть реакция АС на корреляционную функцию ее входа.

Для стационарного входного сигнала : t₁,t₂

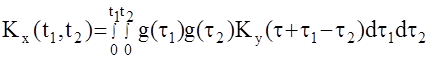
Таким образом, если известны математическое ожидание и корреляционная функция входного сигнала, то всегда можно определить соответствующие характеристики выходного сигнала АС. Однако применение этих формул на практике достаточно сложно, поэтому большой интерес представляет вопрос об их упрощении.

13.7.Каноническое представление случайных процессов.

В ряде случаев случайный входной сигнал может быть представлен в следующем виде 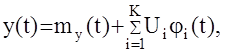здесь U_i- случайные величины, подчиняющиеся условиям

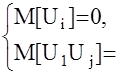
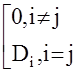
j_i – известные неслучайные функции времени, называемые координатами. В качестве таких координатных функций могут быть sint, cost, e^t, t, …

Представление случайной функции в таком виде называется ее каноническим представлением. Оказывается, что многие реально существующие случайные процессы могут быть представлены в виде канонических представлений: дрейф нуля в усилителях, порывы ветра в турбулентной атмосфере,…

Определим статистические характеристики таких процессов.

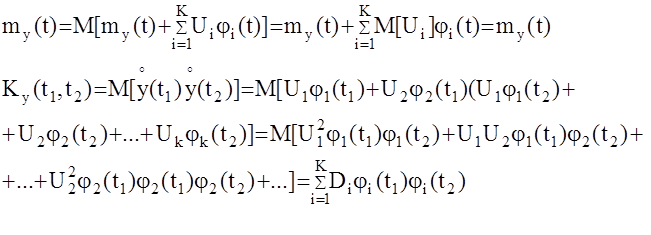
То есть, корреляционная функция кононического случайного сигнала -это сумма произведений дисперсий на соответствующие координатные функции.

Выходной сигнал системы

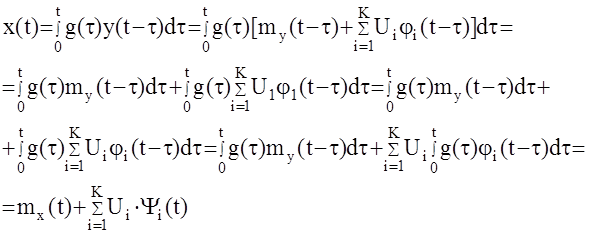
Таким образом, реакция линейной АС на канонический случайный сигнал, представляется также в каноническом виде.

Следовательно, математическое ожидание и корреляционная функция выходного сигнала будет определяться так:

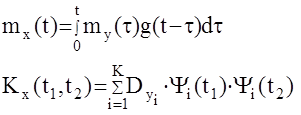то есть не требуют вычисления двойных интегралов. Пример: На вход АС с Ф(р)=1/р действует случайный канонический сигнал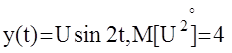

Определить вид выходного сигнала и его статистические характеристики. Очевидно: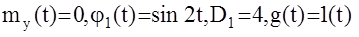

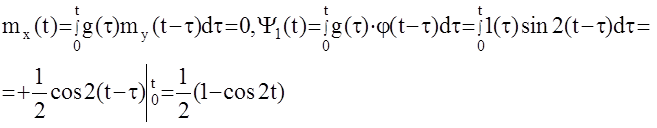
Таким образом , выходной сигнал имеет вид: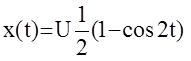

а его корреляционная функция:

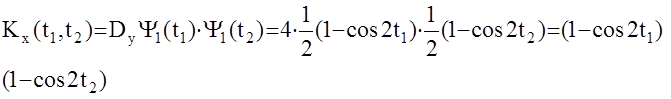
13.8. Условия стационарности выходного сигнала АС.

Пусть на выход линейной АС действует стационарный случайный сигнал y(t) , то есть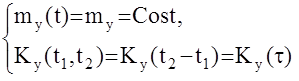

Определим реакцию АС на такой сигнал и условия ее стационарности.

Математическое спадание выходного сигнала

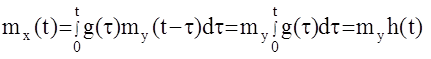где h(t) – переходная функция системы. Корреляционная функция сигнала:

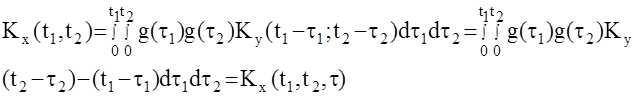
является функцией не только разности аргументов t = t₂-t₁, но и их самих. Таким образом, в общем случае, реакция АС на стационарный случайный сигнал не является стационарной.

Однако для устойчивых АС при достаточно большом времени наблюдения можно записать:

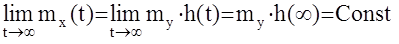
Сonst, в силу устойчивости.

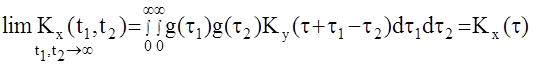
то есть выходной сигнал становится стационарным. Обычно на практике условие стационарности выходного сигнала АС представляют следующим образом:

1). Выходной сигнал АС должен быть стационарным.

2). АС должна быть устойчивой.

3). Время работы системы должно быть больше ее времени регулирования.

13.9.Определение спектральной плотности и дисперсии выходного

стационарного случайного сигнала.

Спектральная плотность есть прямое преобразование Фурье от корреляционной функции. Для стационарных процессов

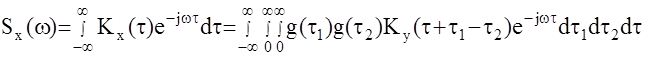
Представим функцию 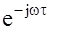в виде 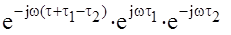и подставим выражение для S_x(w) :

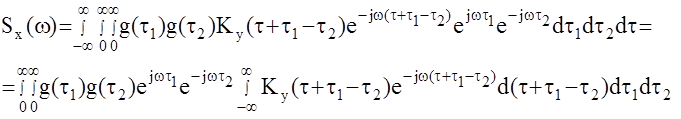
Тогда можно записать:

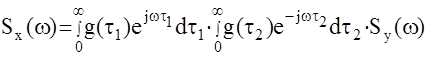вспомним, что

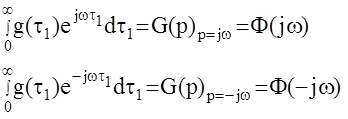
Таким образом :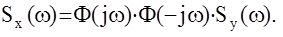

Произведение двух комплексно-сопряженных функций 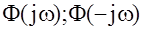есть квадрат модуля этой функции 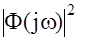или квадрат ее амплитудно-частотной характеристики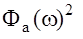

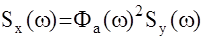
Спектральная плотность выходного установившегося сигнала линейной АС равна произведению квадрата ее амплитудно-частотной характеристики на спектральную плотность входного сигнала.

Определив спектральную плотность, можно определить значение дисперсии и корреляционной функции выходного сигнала.

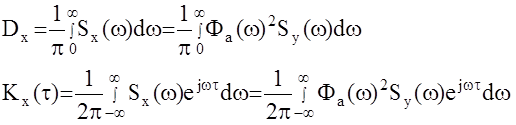
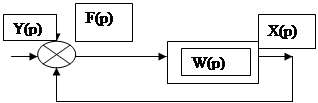
13.10.Метод формирующего фильтра.

Как уже отмечалось, если на вход системы действует белый шум, то вычисление статистических характеристик выходного сигнала существенно упрощается. Однако, белый шум относится к классу физически нереализуемых случайных функций и на входах реальных автоматических систем действуют произвольные случайные сигналы. Возникает вопрос : можно ли преобразовать исходную АС так, чтобы на ее вход действовал белый шум. Пусть структурная схема АС имеет вид:

Здесь Y(p) – детерминированный входной сигнал.

F(p) – случайная помеха – стационарный процесс с заданной спектральной плотностью S_F(w).

Так как система линейная, то выходной сигнал системы можно представить как сумму реакций на детерминированный сигнал y(t) и случайную помеху f(t). Определение реакции на y(t) не составляет труда, и подробно рассматривалось в предыдущих разделах. Поэтому без потери общности можно рассматривать линейную стохастическую АС, как систему на вход которой действуют только случайные входные сигналы.

еперь, для того чтобы рассматривать АС, вход которой – белый шум, реальную помеху f(t) представляют как результат преобразования белого шума некоторым фильтром, который называют формирующим.

Передаточную функцию такого фильтра определяют соотношения:

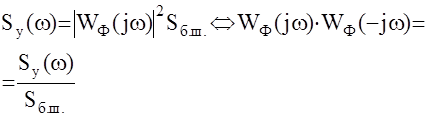
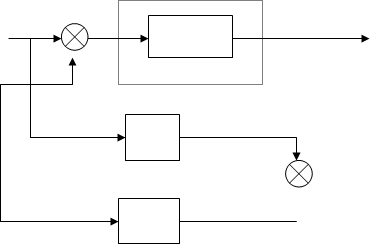
13.11.Прохождение случайных сигналов через нелинейные системы.

Статистическая линеаризация нелинейных элементов.

Пусть на вход нелинейного элемента с функцией передачи f(y)

действует случайный входной сигнал

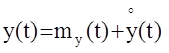В случае, если дисперсия входного сигнала y(t) достаточно мала и его значения выходят за пределы линейного участка, функция передачи f(y), то можно записать:

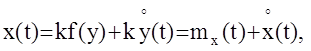
то есть вид выходного сигнала остается прежним. С ростом дисперсии выходного сигнала, его значения начинают выходить за пределы линейного рабочего участка НЭ, что приводит к изменению спектрального состава выходного сигнала, по сравнению с входным, и к изменению даже его закона распределения. Отметим, что статистические характеристики выходного сигнала в этом случае аналитически определить практически невозможно. Как решить эту проблему? Один из возможных путей решения – метод статистической линеаризации, заключающийся в том, что исходный НЭ заменяется эквивалентным по следующей схеме. То есть исходный нелинейный элемент с функцией передачи f(y) заменяется эквивалентным линейным, представляющим собой соединение двух усилительных звеньев с коэффициентами k₀,k₁.

При этом случайный сигнал u(t) с выхода эквивалентного линейного элемента будет иметь следующий вид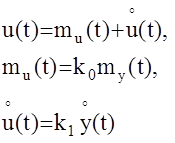

k₀- эквивалентный статистический коэффициент усиления НЭ по математическому ожиданию.

k₁- эквивалентный статистический коэффициент усиления по центрированной случайной составляющей.

Коэффициенты k₀,k₁ очевидно следует выбирать так, чтобы сигналы с выхода НЭ x(t) и с выхода линейного элемента u(t) были в определенной мере статистически эквивалентными. Мера такой эквивалентности обычно определяется с помощью некоторого критерия.

1) Критерий равенства математического ожидания и дисперсии

случайных процессов.

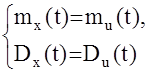
Выведем из этих соотношений значения коэффициентов k₀,k₁.

.

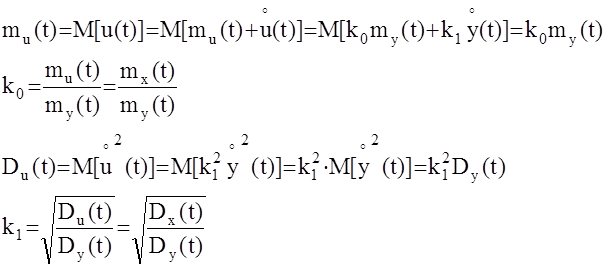
2) Критерий минимума математического ожидания квадрата

ошибкиE(t)=X(t)-u(t).

Введем в рассмотрение интегральную квадратичную оценку

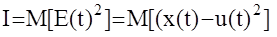
и определим ее минимум по коэффициентам k₀,k₁.

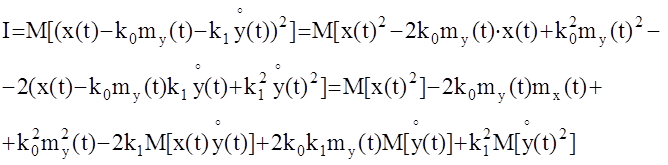Условия экстремума (минимума):

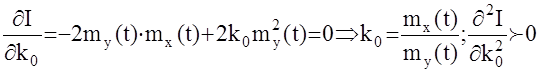
минимум.

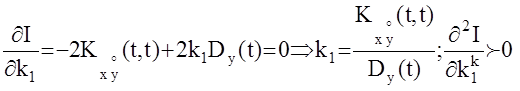-минимум.

Таким образом, можно сделать вывод, что при статистической линеаризации коэффициенты k₀,k₁целиком и полностью определяются и не зависят от вида нелинейности f(x).

Структура системы принимает вид:

Метод формирующего фильтра позволяет моделировать любой случайный процесс с заданной спектральной плоскостью.

13.12.Математическая модель турбулентной атмосферы.

Полет самолета, особенно маневренного на малых высотах, сопровождается различными ветровыми возмущениями, носящими случайный характер. Естественно при анализе и синтезе авиационных АС необходим учет этих возмущений, другими словами математическая модель турбулентной атмосферы. Попробуем сформировать ее. Порывы ветра могут быть разложены на продольную U_x , поперечную U_z и вертикальную U_y составляющие. Спектральные плотности этих составляющих имеют вид (модуль Драйдена):

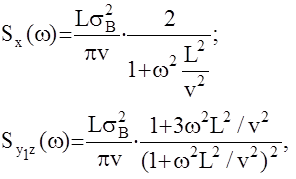
здесь L – масштаб турбулентности (L»100-500м); s_в²- дисперсия случайных порывов ветра; s_в=0-0,5м/с – спокойная атмосфера; s_в=0,5-2,5м/c –средняя турбулентность; s_в>2,5м/c – сильная турбулентность; v- скорость полета м/c (воздушная).

Определим передаточную функцию формирующего фильтра для такой атмосферы ( только для продольной составляющей).

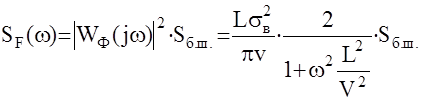
Выделим в данном выражении часть, зависящую от w и представим ее в виде произведения комплексно сопряженных чисел

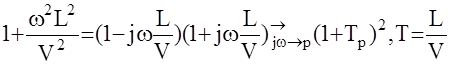
Тогда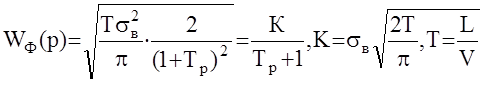

а соответствующее дифференциальное уравнение

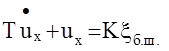
При численном моделировании, сигнал x_б.ш.- белый шум получается на выходе стандартной программы GAUSS – генератора белого шума с заданной интенсивностью S_б.ш.

13.13. Математические модели датчиков информации.

Одним из важнейших вопросов, возникающих при анализе и синтезе авиационных АС, является вопрос измерения вектора состояния объекта, то есть вопрос учета динамики измерительной системы самолета, или другими словами математических моделей датчиков информации: датчиков углов и угловых скоростей, акселерометров, измерителей токов и напряжений, температуры и тому подобное.

Наиболее часто применяемая форма представления оператора датчика имеет вид: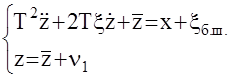

здесь х – измеряемый сигнал,

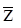-вспомогательная переменная,

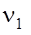- постоянная (медленно-меняющаяся) ошибка датчика, учитывающая величину зоны нечувствительности датчика,

z – выходной сигнал датчика,

x_б.ш. – белый шум, учитывающий флуктвационные ( высокочастотные) ошибки.

Структурная схема АС в этом случае имеет вид

Очевидно, что такая линейная модель датчика характеризуется четырьмя параметрами:

- постоянная времени Т или собственная частота W = 1/Т;

- относительный коэффициент затухания x;

- интенсивность белого шума S_б.ш.

- среднекавдратическое отклонение sn₁- постоянная погрешность измерения.

Приведем значения этих параметров для датчиков, составляющих основу информационной части контуров управления современных самолетов. Здесь X_max – диапозон измерения соответствующего датчика.