автоматических систем.

Оптимальное оценивание координат состояния

14.1.Понятие об алгоритмах оценивания.

В задачах анализа и синтеза АС практически всегда возникает проблема определения координат состояния объекта управления. Обычно непосредственному измерению доступно лишь незначительное число координат, причем измерения z, как правило, производятся с некоторыми случайными ошибками x_t. Отсюда возникает проблема

восстановления вектора состояния объекта Х по результатам доступных измерений z, которую в общем случае будем называть задачей оценивания координат состояния.

Если оценивание осуществляется в детерминированной постановке, то есть без случайных возмущений и помех, то говорят о задаче наблюдения, в противном случае – о задаче фильтрации.

Рассмотрим возможные алгоритмы решения этих задач.

14.2.постановка задачи наблюдения. Наблюдатель Люэнбергера.

Пусть имеется многомерная детерминированная АС вида:

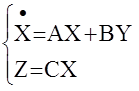
Здесь: X-n-мерный вектор состояния;

Y-m-мерный вектор входных воздействий (управления);

Z-r-мерный вектор измерения (обычно r£n).

Предполагается, что система наблюдаема по Калману, то есть

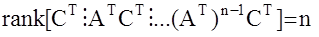
Ставится задача: определить вектор состояния Х по известному вектору измерения Z и входу Y.

Очевидно, решение задачи наблюдения тривиально, если матрица С квадратичная (r=n) и невырожденная. Так как в этом случае

X=C^-1Z

Однако на практике обычно измерителей (датчиков информации) меньше числа координат состояния r<n. Как в этом случае определить вектор состояния Х?

Введем в рассмотрение некоторый наблюдатель, описываемый матричным дифференциальным уравнением

(*)

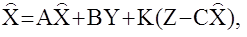здесь: 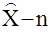-мерная оценка вектора Х, получаемая на основе вектора

измерения Z;

К- неизвестная матрица коэффициентов усиления, размерности

r´n.

Данный наблюдатель получил название наблюдателя Люэнбергера. Матрицу К в этом наблюдателе надо подобрать так, чтобы

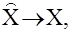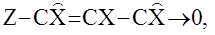тогда а уравнение наблюдателя превращается в уравнение состояния объекта

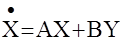
Таким образом, если мы подберем матрицу К так, чтобы

,

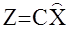то вычисляя 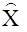на основе реальных измерений Z по формуле (*) мы тем самым найдем (восстановим) неизвестный вектор состояния Х.

Определим теперь алгоритм наблюдения матрицы К. Для этого вычтем из уравнения состояния уравнение наблюдателя (*)

(**)

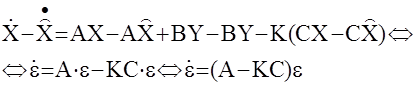
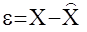Очевидно, что стремление 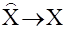означает, что e®0.

Последнее возможно в случае устойчивой системы (**).

Таким образом, матрица К должна выбираться так, чтобы матрица

А-КС была устойчивой (гурвицевой).

Устойчивость А-КС означает, что характеристический полином

det(E_p-A+KC) имеет корни с отрицательными действительными частями.

И так задача восстановления вектора Х по вектору измерения Z сводится к построению наблюдателя Люэнбергера (программирование уравнения (*) на ЭВМ) и выбору матрицы К такой, что матрица А-КС была устойчивой.

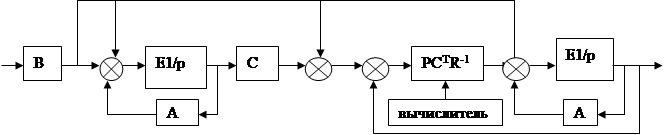
Рассмотрим структурную схему такого наблюдения

То есть на выходе наблюдателя Люэнбергера получается оценка вектора 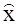, которая при устойчивой матрице А-КС стремится к вектору состояния х. Очевидно, чем быстрее оценка 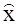сходится к истинному значению вектора состояния х, тем лучше наблюдатель. Скорость сходимости можно увеличить путем повышения запаса устойчивости матрицы А-КС.

14.3. Постановка задачи оптимальной линейной фильтрации.

Непрерывный фильтр Калмана-Бьюси.

Рассмотрим многомерную стохастическую АС вида

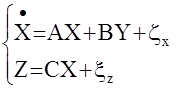Здесь z_х,x_z – векторные некорреляированные белые шумы с диагональными корреляционными матрицами Q и R.(и с нулевыми математическими ожиданиями).

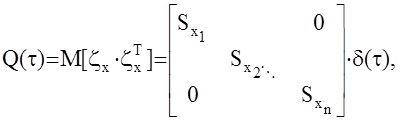
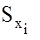- интенсивности скалярных белых шумов .

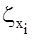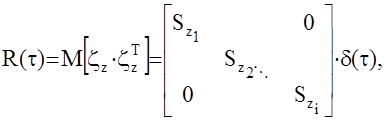
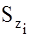- интенсивности скалярных белых шумов .

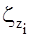Необходимо синтезировать фильтр, выдающий оценку вектора состояния 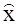, оптимальным образом приближенную к неизвестному вектору состояния Х.

В качестве критерия оптимальности принимается

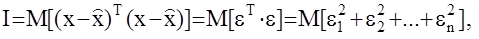то есть минимизируется сумма дисперсий ошибок 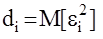оценивания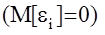

Калманом и Бьюси доказано, что фильтр оптимальный в указанном смысле, имеет структуру наблюдателя Люэнбергера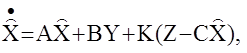

где K=P(t)C^TR^-1-матрица коэффициентов усиления размерности (n´r)

P(t)- матрица, размерности n´n, определяемая из решения матричного дифференциального уравнения Риккати.

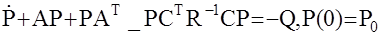
Таким образом, реализация фильтра Калмана предполагает совместное решение на ЭВМ двух дифференциальных уравнений

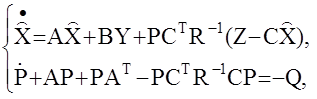
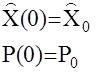
Решаются они на борту ЛА в БЦВМ в реальном масштабе времени.

Общая структура фильтра Калмана-Бьюси имеет вид:

Объект наблюдения Фильтр Калмана-Бьюси

В результате работы фильтра на его выходе получается оценка 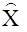, которая оптимальным образом приближается к искомому состоянию Х.

Однако процесс сближения во – многом определяется правильностью задания параметров фильтра: корреляционных матриц Q, R, начальных условий 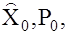эффективности вычислительной процедуры решения уравнений Риккати.

14.4.Дискретный фильтр Калмана.

Оценки вектора состояний объекта при использовании фильтра

Калмана являются функциями времени, и поэтому в большинстве случаев предпочтение отдается рекуррентным процедурам оценивания, позволяющим вычислять оценки 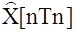по мере поступления измерений .

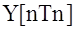Дискретное рассмотрение приводит к аглебраизации решения задачи, то есть а исключению интегрирования нелинейных дифференциальных уравнений системы, позволяющее получать рекуррентные аналитические соотношения, а следовательно, и упрощение вычислительных процедур.

Рассмотрим построение алгоритма с использованием рекуррентного метода оценивания с минимальной дисперсией. Он наиболее удобен, поскольку не требует никаких предварительных теоретических выкладок и допускает простую и наглядную интерпретацию результатов.

Предварительно рассмотрим взвешенное усреднение двух векторных величин.

1.)Алгоритм оценивания, известный как фильтр Калмана, формирует взвешенное среднее двух независимых векторных оценок.

Предположим, для некоторого m – мерного вектора х найдены две статистические независимые оценки 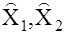. Их взвешенным средним назовем величину 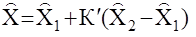(13.8.) Где 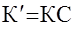-весовая матрица (m´m), которая выбирается таким образом, чтобы дисперсия

(или СКО) оценки 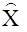была минимальна.

Рассмотрим динамическую систему состоящую из объекта наблюдения плюс фильтр Калмана, для которой введем обозначения:

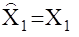- вектор состояния объекта;

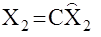- вектор выходных измерений, откуда 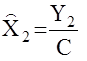. С учетом этого, уравнение (13.8.) примет вид 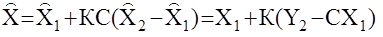(13.9.)

Необходимо искать оценку 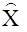вектора состояний, которая минимально (в вероятностном смысле) отличалась бы от х, то есть обеспечила минимум дисперсии.

2). Применим описанную процедуру к оцениванию вектора состояния Х[(n+1)Tn] марковского процесса

X[(n+1Tn]=AX[nTN]+FV[nTn] ;

Y[(n+1)Tn]+CX[(n+1)Tn]+N[(n+1)Tn]; (13.10)

где V[nTn] и N[(n+1)Tn]- случайные процессы в виде белого шума.

Представление такое же как и в фильтре Калмана-Бьюси. В уравнении (13.9) обозначим:

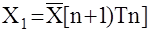- значение 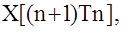предсказанное на основе ранее полученной оценки 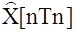. Предсказанное значение вектора состояния определяется по формуле 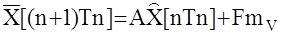(13.11)

В этом выражении вместо неизвестной точной величины V[nTn] использовано ее математическое ожидание m_V;

Y₂=Y[(n+1)Tn] – новое измерение выхода.

С учетом введенных обозначений рекуррентный алгоритм оценивания приобретает вид:

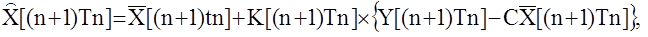
где K[(n+1)Tn] – матрица коррекции. (13.12)

3) Определение матрицы коррекции.