Идентификация параметров автоматических систем.

15.1. Основные определения. Понятие о методах идентификации.

Успешное управление любым объектом предполагает наличие достаточно полной информации о характеристиках этого объекта или, говоря конкретно, о структуре и параметрах его математической модели. Опыт, накопленный при проектировании систем управления, убедительно свидетельствует о том, что нельзя построить математическую модель, адекватную реальной системе, только на основе теоретических исследований физических процессов в системе. Сформулированная таким образом математическая модель, как правило, отличается от реальной системы, что приводит соответственно к снижению качества управления. Поэтому в процессе проектирования систем управления одновременно с теоретическими исследованиями проводят многочисленные эксперименты по определению и уточнению математической модели системы.

Идентификацией называется определение параметров и структуры

математической модели, обеспечивающей наилучшее совпадение

выходных координат модели и процесса при одинаковых входных

воздействиях.

В зависимости от объема априорной информации об идентифицируемом процессе различают идентификацию в широком и узком смысле. В первом случае информация об объекте или незначительна или вообще отсутствует. Во втором – считается известной структура системы и класс моделей, к которому она относится. Для авиации характерным является достаточно полное знание структур и класса идентифицируемых объектов, поэтому в дальнейшем под общим термином ,,идентификация'' будем понимать ее разновидность в узком смысле, то есть определение параметров математической модели заданной структуры.

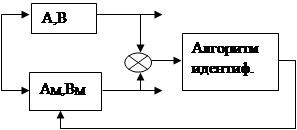
Все эти методы идентификации по способу организации вычислительных процедур могут быть подразделены на два больших подкласса: прямые и адаптивные. Первые из них предполагают непосредственное определение параметров математической модели объекта по результатам измерения его векторов входа Y и выхода Х на некотором интервале времени.

Адаптивные алгоритмы предполагают настройку коэффициентов некоторой модели, той же структуры, что и идентифицируемый процесс, до тех пор, пока векторы выхода объекта X и модели X_M не совпадут.

Прямые алгоритмы характеризуются относительной простотой, но и невысокой точностью вычислений. Адаптивным же алгоритмам присуща высокая точность, за счет непрерывности процесса настройки, но и относительная сложность и громоздкость в реализации. Рассмотрим наиболее часто применяемые на практике алгоритмы идентификации. Предварительно отметим, что предполагается ,что для исходного объекта выполняются условия идентифицируемости.

15.2. Прямые вычислительные алгоритмы идентификации.

1)Метод наименьших квадратов (МНК)

Для объекта 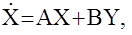dimX=n, dimY=m

по результатам наблюдения за векторами входных Y и выходных Х координат объекта определить неизвестные параметры матриц А и В.

Перепишем данное уравнение в виде

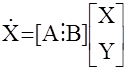-расширенный вектор состояния размерности (n+m)

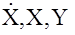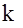Измерим вектора в дискретных моментах времени t₁,t₂,…,t_k и запишем соответствующие уравнения

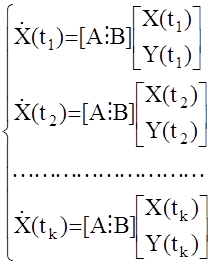
или в матричной форме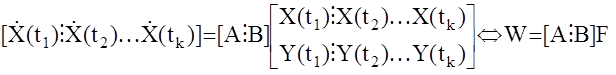

Если число измерений k совпадает с (n+m), то матрица F становится квадратной и задача идентификации решается просто

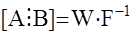в случае невырожденной матрицы F.

Пример: Рассмотрим объект вида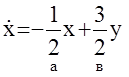

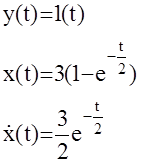Допустим, что а и в неизвестны, и необходимо их определить по результатам измерения 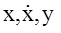в момент времени t₁=0, t₂=2c

t₁=0 y(0)=1, x(0)=0,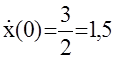

t₂=2 y(2)=1,

x(2)=3×(1-e^-1)=3×0,63=1,89,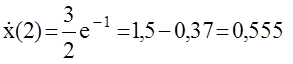

Составим уравнение идентификации:

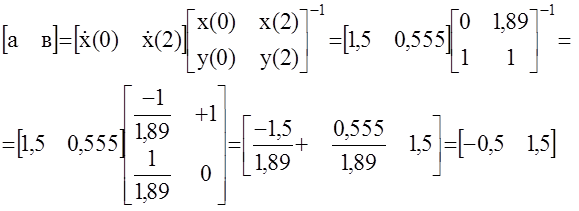
Таким образом, по результатам измерения входных и выходных сигналов удалось точно определить неизвестные параметры ее математической модели.

Однако следует отметить, что в реальных условиях измерения осуществляются с погрешностями, что приводит к довольно значительным ошибкам идентификации. Для устранения этого делают число измерений k больше, чем размерность расширенного вектора состояния (n+m). В этом случае доказано, что оценка (приближенное значение) матрицы 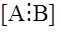определяется по формуле

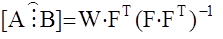и при этом минимизируются квадраты ошибок идентификации 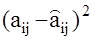, почему данный алгоритм и получил название метода наименьших квадратов.

Достоинство метода – его простота, недостатки – двойной комплект датчиков, (для измерения вектора состояния и его производной) высокие требования к их точности и достаточно большое число необходимых измерений.

2) Метод интегральных оценок.

Попробуем устранить недостатки метода наименьших квадратов за счет использования интегральных оценок от координат состояния, а не собственно самих координат в дискретные моменты времени.

Вновь рассмотрим объект

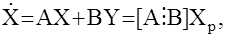
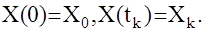
Введем в рассмотрение некоторую устойчивую модель с известными коэффициентами

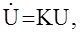
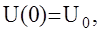
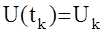
где k- устойчивая, обычно диагональная матрица, размерности (n+m)´ (n+m).

Умножим уравнение объекта справа на U^T, а уравнение модели протранспонируем и умножим слева на Х:

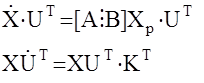
Данные уравнения сложим и проинтегрируем на интеграл от 0 до t_k

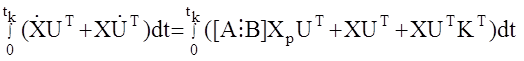
в итоге получим: 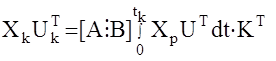и окончательно

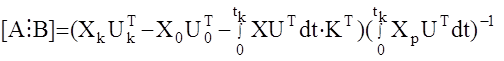
Данная формула является расчетной для метода интегральных оценок. Как видим в данном методе необходимо измерять только сам вектор состояния на определенном интервале времени [0,t_k], а использование интегральных оценок от координат состояния позволяет существенно снижать требования к точности их измерения за счет сглаживающих свойств интеграла (фильтр низких частот).

15.3.Адаптивные алгоритмы идентификации.

Эти алгоритмы предполагают настройку коэффициентов некоторой модели той же структуры, что и идентифицируемый объект. Законы настройки являются аналитическим выражением адаптивных алгоритмов идентификации.

1) Метод функций Ляпунова.

Предложен американским ученым К.С.Нарендрой (родился в 1933г. в Индии) и П.С.Валавани (родился в 1952г. в Греции) в 1978году.

Для линейного детерминированного объекта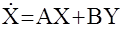

и настраиваемой модели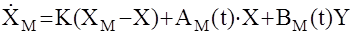

где К – известная устойчивая матрица. Требуется определить законы настройки матриц А_М и В_М, такие что

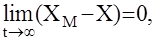
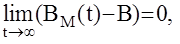
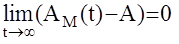
Перейдем от пространства состояний, характеризуемого векторами состояния Х и модели Х_М, к пространству ошибок, характеризуемого ошибками Е=Х_М-Х, DА=А_М(t)-A, DB=B_M(t)-B. Для этого вычтем из уравнения модели уравнение состояния

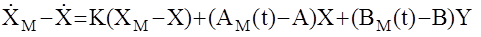или

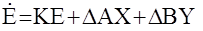
Задача идентификации в этом случае сводится к задаче обеспечения асиметической устойчивости объекта в пространстве (Е,DА,DВ). Решают ее на основе второго метода Ляпунова. Как обычно, назначается положительно определенная скалярная функция

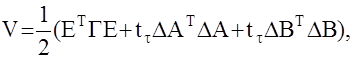где t_t- след соответствующей матрицы – сумма ее диагональных элементов и берется от нее полная производная на уравнениях движения системы. Опуская промежуточные вычисления, получаем, что искомые законы уравнения имеют вид: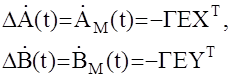

где Г- положительно определенное решение уравнения Ляпунова

ГК+К^ТГ=-b,

b- заданная положительно определенная матрица весовых коэффициентов.

Данные законы и определяют алгоритм идентификации. Основной недостаток его в том, что условия асимптотической устойчивости, то есть точной сходимости А_М(t)®A и В_М(t)®B выполняются только для определеного вида входных сигналов Y(t).

2) Алгоритм идентификации на основе фильтра Калмана.

Этот алгоритм, а точнее целая группа алгоритмов, были предложены А.А.Красовским в середине 80-х годов. Они получили в настоящее время наиболее широкое распространение на практике, особенно при идентификации многомерных нелинейных объектов вида

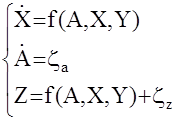
Здесь полагается, что векторы Х и Y известны, вектор 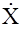измеряется с некоторым шумом z_Z, а неизвестные ( идентифицируемые) параметры вектора (матрицы) А, подвержены "дрейфу", характеризуемому белым шумом z_а.

В этом случае оценка 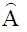определяется на основе нелинейного фильтра Калмана вида

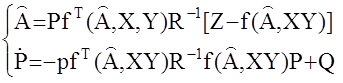
Здесь R,Q- матрицы интенсивностей белых шумов z_а и z_Z соответственно.

Отметим, что недостатком данного алгоритма является необходимость измерения производных вектора состояния объекта и точного значения самого вектора состояния, что трудно реализовать на практике.