Оптимизация систем автоматического управления.

16.1. Постановка задачи оптимального управления.

Появление и быстрое развитие вычислительной техники, внедрение ее в практику конструкторских и инженерных расчетов открыло дорогу широчайшему внедрению многих выдающихся достижений математики, в частности теории оптимального управления многосвязными объектами.

Оптимальной называется автоматическая система, которая является лучшей в смысле выбранного критерия качества.

Математической основой теории оптимального управления является вариационное исчисление, у истоков которого стояли знаменитые математики и механики 17-18 веков братья Бернулли, Эйлер, Лагранж. Собственно теория оптимального управления, как отдельная наука определилась в середине пятидесятых годов нашего века открытием академика Понтрягина и его учеников так называемого принципа максимума. Дальнейшее развитие этой теории связано с именами А.М. Петрова, Р. Калмана, А.А.Красовского и целого ряда других.

В общем виде задача оптимального управления может быть сформулирована следующим образом:

1) Автоматическая система описывается дифференциальным матричным нелинейным уравнением, разрешенным относительно первой производной (форма Коши):

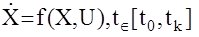, (1)

где Х- n - мерный вектор состояния объекта;

U- m - мерный вектор управления.

2) Требуется обеспечить экстремум (обычно минимум) некоторому

функционалу качества 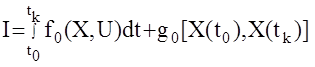, (2)

где f₀(X,U) – некоторая скалярная функция, определяющая требования к качеству переходных процессов и "расходу органов управления";

g₀[X(t₀), X(t_k)] – терминальная составляющая функционала, определяющая требования к начальному и конечному состоянию управляемого объекта.

3) Полученные управления и фазовые коэффициенты должны удовлетворять некоторым ограничениям, обычно задаваемым в виде неравенств U(t)£ U_max, X(t)£X_max.

4) Задается метод оптимизации (метод нахождения управлений U, экстремизирующих функционал I).

Решение этой задачи методом классического вариационного исчисления предполагает решение уравнения (1) аналитическим способом, подстановку его в функционал (2) и нахождение экстремума функционала по U. Основная проблема при таком подходе в том, что, во-первых, вектора состояния Х и управления U связаны между собой уравнением (1). Поэтому необходимо совместное решение системы матричных уравнений 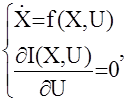что возможно лишь для простейших систем и определенных видов функций f.

Во-вторых, оптимальные управления получаются в виде функций времени U_опт=U_опт(t) и могут принимать сколь угодно большие значения, не удовлетворяя принятым ограничениям. Поэтому, вообще говоря, вариационное исчисление не относится к классу методов оптимального управления.

16.2.Критерий оптимизации.

Рассмотрим теперьфизический смысл отдельныхсоставляющих функционала качества.

а) интегральная составляющая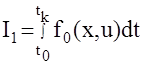

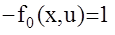, тогда: При минимизации такой составляющей будет очевидно минимизироваться время достижения конечного состояния t_k , то есть строится система с максимальным быстродействием;

-f₀(x,u)=x², тогда получили уже известную нам интегральную квадратичную оценку - один из косвенных критериев качества системы. Его минимизация улучшает характеристики качества системы.

–f₀(x,u)=x²+u², тогда 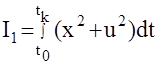- при минимизации такой составляющей оптимизируется качество системы, но уже с учетом расходов органов управления.

Могут применяться и другие виды интегральных составляющих функционала: все зависит от цели управления и возможности связать эту цель с видом функционала;

б) внеинтегральная составляющая I₂=g₀[x(t₀),x(t_k)],

-g₀[x(t₀),x(t_k)]=0 - в этом случае решается нетерминальная задача оптимального управления: требований к начальному и конечному состоянию нет. Во – многих задачах такое допущение существенно упрощает процедуру синтеза оптимальных управлений.

-g₀[x(t₀), x(t_k)]=rx²(t_k) – определены требования к конечному состоянию в виде квадратичной формы. Такой вид g₀ позволяет достигать желаемого конечного состояния с помощью линейных оптимальных управлений.

16.3.Принцип максимума Понтрягина.

Для решения поставленной задачи оптимального управления воспользуемся общим принципом Лагранжа, который можно сформулировать так:

- для того, чтобы найти экстремум некоторой функции связанных между собой переменных, надо прибавить к этой функции такую функцию, которая обращается в ноль на уравнениях связи переменных, умножить ее на некоторые неопределенные множители, а потом, искать экстремум полученной суммы так, если бы эти переменные были бы независимыми.

Полученные в результате таких преобразований уравнения будут служить совместно с уравнениями связи для определения всех неизвестных, то есть неопределенных множителей и собственно оптимальных управлений.

В качестве такой функции, для которой ищется экстремум, выберем функционал (2). В соответствии с принципом Лагранжа преобразуем его в следующую сумму, которую будем называть лагранжианом ,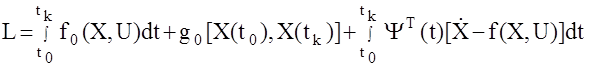

где - вектор неопределенных множителей Лагранжа, размерности n.

Очевидно, что на уравнениях движения исходной системы (1), вторая интегральная составляющая обращается в ноль. Следовательно, если мы найдем экстремум L по U, то эти же уравнения обеспечат экстремум I, но для конкретного объекта (1). Поиск экстремума L по U будем осуществлять в предположении независимости X и U, согласно принципу Лагранжа.

Преобразуем последнюю составляющую лагранжиана с учетом правила интегрирования по частям: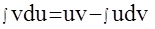

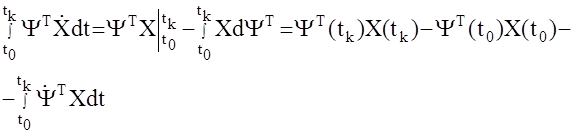
Лагранжиан перепишется так:

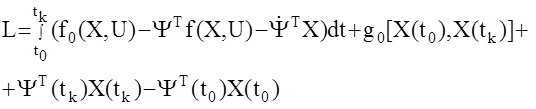
Введем в рассмотрение следующую скалярную функцию

называемую функцией Гамильтона или гамильтонианом. Тогда:

Необходимые условия экстремума L по независимым переменным X и U можно представить так:

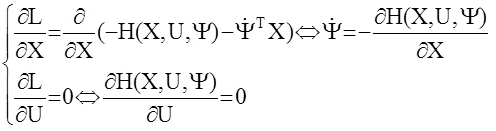
Добавим к этим уравнениям уравнение связи (1) и получим

U£U_max

Получили систему трех уравнений относительно трех неизвестных X,U,Y, что показывает ее совместность, то есть принципиальную возможность точного решения задачи оптимального управления. Однако необходимо отметить следующее: так как лагранжиан L в общем случае имеет внеинтегральную составляющую

, определяющуюся начальными и конечными значениями векторов Х и Y, то при решении полученной системы уравнений необходимо, чтобы начальным значениям X(t₀),Y(t₀) соответствовали заданные конечные условия X(t_k),Y(t_k). То есть необходимо решать так называемую двухточечную краевую задачу. В настоящее время решение данной задачи в аналитическом виде удается получить лишь в редких случаях для систем не выше второго порядка. Поэтому приходится ее решать путем перебора, то есть задаются начальные условия X(t₀), Y(t₀) решается система уравнений до момента t_k и определяются X(t_k), Y(t_k), если X(t_k) не соответствует заданному значению, выбирается новое значение Y(t₀) и повторяется решение до тех пор, пока не попадем в заданное положение X(t_k).

Сложность или невозможность получения аналитических результатов для задач в более общей постановке с использованием принципа максимума привели к развитию вычислительных и приближенных методов оптимального управления, которые будем рассматривать ниже.

16.4.Метод динамического программирования.

Метод динамического программирования, предложенный в начале 50-х годов американским ученым Р. Беллманом, предполагает решение поставленной общей задачи оптимального управления несколько иным, чем в принципе максимума, способом. Основывается динамическое программирование на принципе оптимальности Беллмана, который можно сформулировать так:

Оптимальное управление определяется только конечной целью управления и состоянием системы в рассматриваемый момент времени, независимо от того, каким образом система пришла в это состояние.

То есть если траектория x=f(t),tÎ[t₀,t_k] является оптимальной, то любая ее часть x=f(t),

tÎ[t,t_k], приводящая к конечному состоянию Х_k является также оптимальной траекторией.

Итак, объект описывается обычной системой дифференциальных уравнений с жестко заданными начальными условиями

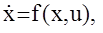
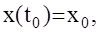
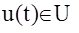
Требуется найти уравнения u = u_опт, обеспечивающие минимум функционалу 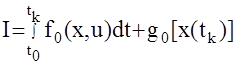. Введем в рассмотрение некоторую функцию 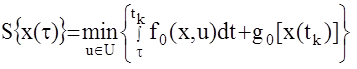, (1)

определенную на оптимальной траектории x_опт(t), t£t£t_k. Отметим, что 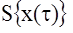не зависит от управления u(t), а только от х(t) - начала интервала оптимизации. Разобьем отрезок времени [t, t_k] на два [t,t+D], [t+D,t_k] где D- сколь угодно малая величина. Тогда (1) представима в виде .

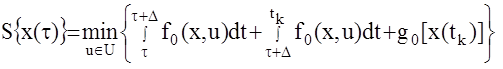В соответствии с принципом оптимальности часть

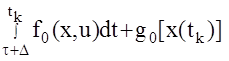принимает на оптимальной траектории минимальное значение, следовательно, она может быть обозначена как

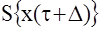получили:

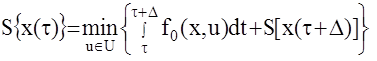(2)

Так как D- сколь угодно малая величина, то (метод прямоугольников)

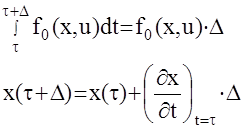(ряд Тейлора с первым членом). Учтем, что

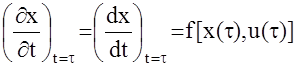тогда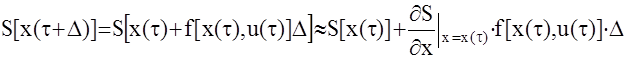

Таким образом,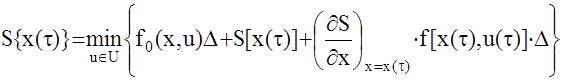

Так как S{x(t)} не зависит от управления u(t), то она может быть вынесена за знак минимума, тогда

(3)

Данное уравнение называется функциональным уравнением Беллмана, позволяющим определять оптимальное уравнение u_опт(t). Очевидно, минимум выражения в квадратных скобках достигается либо при условии, что его производная по управлению u равна нулю, либо само выражение равно нулю при любых u, то есть

исключим из данной системы 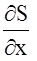и получим 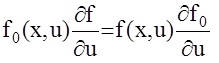. (4)

Из решения данного уравнения и определяется оптимальное уравнение

u = u_опт

Пример: дан электродвигатель постоянного тока с независимым возбуждением где w - угловая скорость вращения;

u_y – управляющее напряжение.

Требуется определить оптимальный закон управления 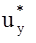, минимизирующий функционал .

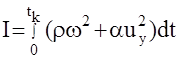Для данной задачи очевидно 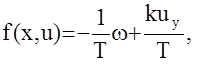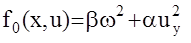Составим уравнение (4)

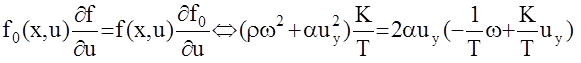
получаем: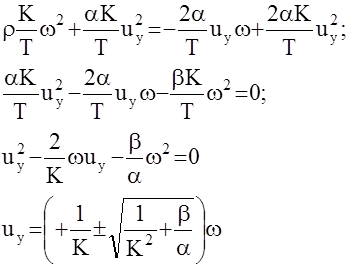

Как видим, управление получается в виде обратной связи по состоянию объекта. Это одно из основных достоинств метода динамического программирования по сравнению с принципом максимума. Однако, для многомерных систем и ограничений решение уравнения (4) в явном виде получить сложно. В этом случае приходится применять численное интегрирование (4) в реальном времени.

16.5 Аналитическое конструирование систем оптимального управления

Среди направлений теории оптимального управления своей практической результативностью, особенно для многомерных систем выделяется направление, получившее название аналитическое конструирование регуляторов (АКР). Термин аналитическое означает, что в данном методе заранее известно аналитическое (формульное) выражение для оптимального управления u_опт(t) и требуется определить только параметры этого выражения. Впервые данный термин был введен академиком А.М. Летовым в 1960 г. Рассмотрим методы АКР для линейных многомерных объектов.

1) Метод Летова – Калмана

Для линейного стационарного детерминированного объекта, описываемого матричным дифференциальным уравнением

(1)

требуется определить управление u, доставляющее минимум функционалу:

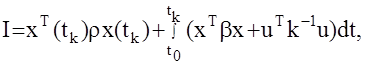(2)

где x^T(t_k)rx(t_k) - терминальная составляющая, определяющая требования к конечному состоянию объекта;

r, b, k - заданные, положительно определенные, симметричные матрицы коэффициентов функционала.

Рассмотрим положительно определенную квадратичную форму от фазовых координат объекта:

V = x^TГх, где Г – некоторая неизвестная матрица коэффициентов, и определим её полную производную на уравнениях объекта (1).

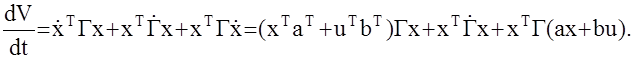
Допустим, что искомое оптимальное управление имеет вид:

u = u_опт = -kb^TГх (3)

Подставим это выражение в формулу для производной.

Потребуем, чтобы:

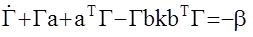(4)

тогда:

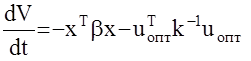(5)

В силу положительной определенности матриц b и k получили, что производная есть функция отрицательная. Поэтому, согласно 2-му методу Ляпунова замкнутая АС с управлением u_опт является асимптотически устойчивой. Уравнение (4) называется матричным дифференциальным уравнением Риккати – его решение (матрица Г) определяет неизвестные параметры оптимального закона управления u_опт. Причем матрица Г получается положительно определенной независимо от того устойчива или неустойчива исходная система.

Докажем теперь, что управления u_опт обеспечивают не только устойчивость замкнутой системы, но и доставляют минимум заданному функционалу качества (то есть являются оптимальными). Для этого проинтегрируем выражение (5):

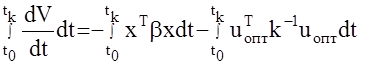или

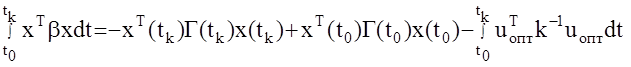
Подставим данный интеграл в выражение для I

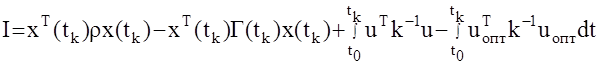
Так как I функция по определению неотрицательная, то ее абсолютный минимум (ноль) достигается при и 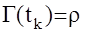.И так, полученный результат можно сформулировать в виде следующей теоремы.

Теорема Летова-Калмана: Для объекта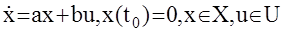

оптимальными в смысле минимума функционала

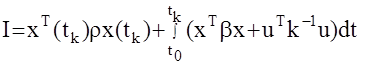служат управления

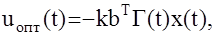где Г(t)- положительно определенная матрица-

решение уравнения Риккати 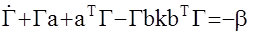при граничном условии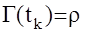

Итак, процедура определения оптимального управления сводится к решению нелинейного дифференциального уравнения Риккати в обратном времени при граничном условии 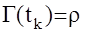, в запоминании полученной программы Г(t) и ее реализации в реальном времени. Отметим, что данная вычислительная процедура существенно упрощается при решении нетерминальных задач оптимального уравнения (когда не заданы требования к конечному состоянию объекта и времени оптимизации), то есть 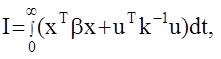(t_k=¥ и x(t_k)rx(t_k) = 0 в силу устойчивости). В этом случае оптимальный закон получается стационарным (Г(t)=const) 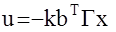, а матрица Г является решением уже алгебраического решения Риккати ( 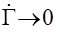, вынужденное решение)

.

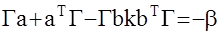2) Метод А.А. Красовского

Данный метод получивший название АКР по критерию обобщенной работы был предложен Александром Аркадьевичем Красовским в 1968 году. Сущность метода заключается в видоизменении функционала качества

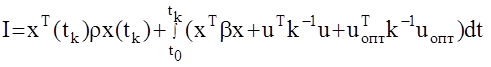
путем добавления интегральной составляющей 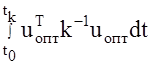, определяющей ограничения на управления уже в оптимальной системе. Поскольку оптимальные управления на этапе задания требований к системе (функционала) еще не известны, то функционал получается полуопределенным, хотя и имеет ясный физический смысл. Но такой искусственный прием позволил существенно снизить вычислительные трудности рассматриваемого метода.

Выведем основные расчетные соотношения для данного метода применительно для того же линейного объекта:

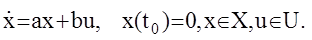(1)

Вновь введем в рассмотрение положительно определенную квадратичную форму V= х^ТГх и определим её полную производную на уравнении движения объекта (1).

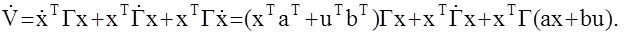
Примем, что оптимальное управление имеет вид:

u_опт = -kb^TГх,

тогда:

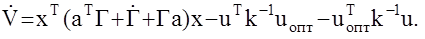
Очевидно, что знакоотрицательна тогда и только тогда, когда выполняются два условия: u = u_опт и 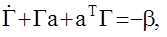где b - положительно определенная матрица. Последнее уравнение нам уже известно, как уравнение Ляпунова, встречающееся в теории устойчивости. Так, согласно второму методу Ляпунова его решение (матрица Г) будет положительно определенной (в соответствии с постановкой задачи оптимального управления) лишь в том случае, когда исходный объект (его матрица а) устойчива. Таким образом, оптимизация по критерию обобщенной работы в отличие от метода Летова-Калмана, предполагает априорную устойчивость исходного объекта, что сужает область применения метода.

Докажем теперь, что управление u_опт доставляют минимум функционалу I . Для этого используем тот же прием, что и при доказательстве в методе Летова-Калмана.

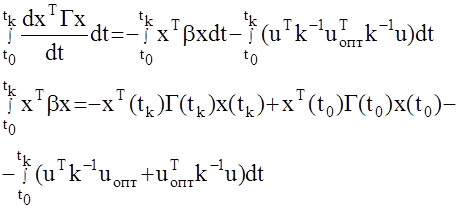
Подставим данное выражение в I

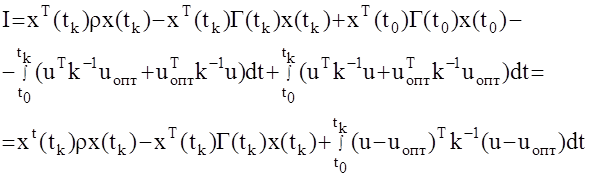
Итак получаем, что абсолютный минимум I достигается при u=u_опт и

Г(t_k)=r. Вновь сформулируем полученный результат в виде теоремы.

Теорема А.А. Красовского. Для линейного детерминированного устой -

чивого объекта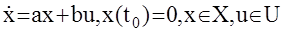

оптимальными в смысле минимума функционала

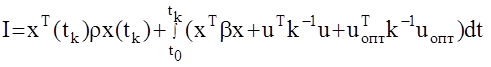являются

уравнения где Г – положительно определен -

ная симметричная матрица- решение линейного матричного диф-

ференциального уравнения Ляпунова. 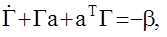при крае -

вом условии Г(t_k)=r.

Отметим, что в случае нетерминальной задачи (t_k=¥) управление u_опт получается стационарным u_опт=-kb^TГх, а матрица Г определяется из решения уже алгебраического уравнения Ляпунова Га+а^ТГ=-b, методы решения которого достаточно хорошо разработаны.

16.6. Сравнительная характеристика методов оптимального управления.

Такую сравнительную оценку проведем с трех позиций: класс оптимизируемых объектов, вычислительные трудности применения того или иного метода и возможность практической реализации синтезируемых управлений.

Область применения принципа максимума Понтрягина включает в себя широчайший класс нелинейных нестационарных объектов с достаточно общими ограничениями на фазовые координаты, управления, время и т.д. Однако для него характерны значительные вычислительные трудности, связанные прежде всего с необходимостью решения двухточечной краевой задачи для системы сопряженных уравнений. Кроме того, оптимальные управления получаются в виде сложных нелинейных законов или программ, что не всегда удобно реализовать на практике. В этой связи более предпочтительным оказывается динамическое программирование, в котором оптимальный закон управления получается в виде обратной связи по координатам состояния, что легко практически реализуемо. Однако необходимость решения функционального уравнения Беллмана (в частных производных), неоднозначность получаемого решения приводит к существенным вычислительным трудностям.

Аналитическое конструирование Летова-Калмана-Красовского дает достаточно простой путь реализации оптимального закона управления (в виде аналитической линейной функции от координат объекта) и при этом обеспечиваются сравнительно невысокие вычислительные трудности, связанные с решением уравнений Риккати и Ляпунова. Но в настоящее время эти методы в основном ограничиваются классом линейных объектов и достаточно узким кругом возможных ограничений.

Обобщая все вышесказанное, можно сказать, что применение того или иного метода зависит от поставленной задачи, особенностей объекта управления, характеристик применяемых вычислительных средств и, естественно от способности инженера-конструктора правильно формализовать поставленную задачу и сделать выбор соответствующего метода оптимального управления.