Схемы и линейные программы.
Указанное выше свойство характерно и для программ, в которых один раз вычисленное выражение можно использовать неоднократно. Рассмотрим один из простейших классов программ – линейные (неветвящиеся) программы. Такие программы представляют последовательности присваиваний вида: 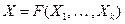 , где
, где 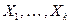 – переменные,
– переменные, 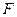 – имя
– имя 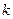 -местной базисной функции.
-местной базисной функции.
В случае нашего базиса 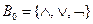 линейная программа состоит из присваиваний вида:
линейная программа состоит из присваиваний вида:
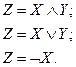
Линейная программа 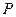 с выделенными входными переменными
с выделенными входными переменными 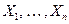 порождает для каждого набора
порождает для каждого набора 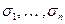 значений входных переменных естественный процесс вычисления: вначале переменным
значений входных переменных естественный процесс вычисления: вначале переменным 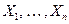 присваиваются значения
присваиваются значения 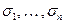 соответственно, а каждой из остальных переменных присваивается значение ноль. Затем последовательно выполняются присваивания программы
соответственно, а каждой из остальных переменных присваивается значение ноль. Затем последовательно выполняются присваивания программы 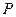 , в результате чего каждая из переменных
, в результате чего каждая из переменных 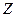 программы получает заключительное значение:
программы получает заключительное значение: 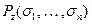 .
.
Определение 11.9. Скажем, что программа 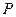 с входными переменными
с входными переменными 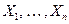 вычисляет в выходной переменной
вычисляет в выходной переменной 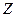 функцию
функцию 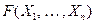 , если для любого набора значений входов
, если для любого набора значений входов 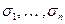 после завершения работы
после завершения работы 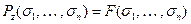 .
.
Между схемами и линейными программами имеется тесная связь.
Теорема:
1. По каждой логической схеме 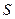 со входами
со входами 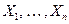 и функциональными элементами
и функциональными элементами 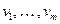 можно эффективно построить линейную программу
можно эффективно построить линейную программу 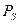 с входными переменными
с входными переменными 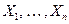 и рабочими переменными
и рабочими переменными 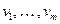 , которая в любой переменной
, которая в любой переменной 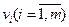 вычисляет функцию
вычисляет функцию 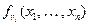 .
.
2. По каждой линейной программе 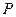 с входными переменными
с входными переменными 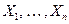 , вычисляющей в выходной переменной
, вычисляющей в выходной переменной 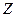 некоторую функцию
некоторую функцию 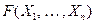 можно эффективно построить логическую схему
можно эффективно построить логическую схему 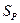 со входами
со входами 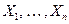 , в которой имеется вершина
, в которой имеется вершина 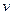 такая, что
такая, что 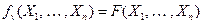 .
.
Доказательство:
Пусть 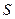 – схема со входами
– схема со входами 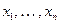 и функциональными элементами
и функциональными элементами 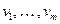 . Построим по ней линейную программу
. Построим по ней линейную программу 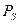 с входными переменными следующим образом: упорядочим все входные и функциональные вершины
с входными переменными следующим образом: упорядочим все входные и функциональные вершины 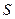 по глубине (вершины одной глубины в любом порядке) –
по глубине (вершины одной глубины в любом порядке) – 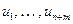 . Программа
. Программа 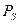 будет последовательностью
будет последовательностью 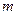 присваиваний.
присваиваний.
Пусть вершина 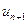 помечена
помечена 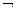 и в неё входит ребро из
и в неё входит ребро из 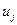 . Тогда в качестве
. Тогда в качестве 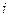 -й команды поместим в
-й команды поместим в 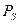 присваивание
присваивание 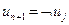 .
.
Пусть вершина 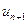 помечена некоторым символом из множества
помечена некоторым символом из множества 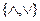 и в неё входят ребра из
и в неё входят ребра из 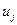 и
и 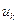 . Тогда в качестве
. Тогда в качестве 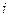 -й команды поместим в
-й команды поместим в 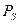 присваивание
присваивание 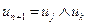 или
или 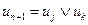 . Упорядочение вершин по глубине гарантирует, что
. Упорядочение вершин по глубине гарантирует, что 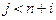 и
и 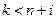 . Поэтому при вычислении
. Поэтому при вычислении 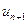 значения аргументов уже получены и индукцией по глубине легко показать, что для каждого
значения аргументов уже получены и индукцией по глубине легко показать, что для каждого 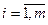 программа
программа 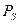 вычисляет в переменной
вычисляет в переменной 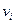 функцию
функцию 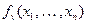 .
.
Пример:
Применим конструкцию теоремы к схеме 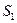 , представленной на рис.1. Её вершины можно упорядочить по глубине так:
, представленной на рис.1. Её вершины можно упорядочить по глубине так: 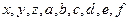 . Порождая команды по описанным выше правилам, полагаем следующую линейную программу
. Порождая команды по описанным выше правилам, полагаем следующую линейную программу 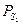 :
:
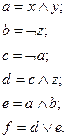
| <== предыдущая лекция | | | следующая лекция ==> |
| Отношения. Свойства отношений. | | | Булева алгебра. Основные операции булевой алгебры. |
Дата добавления: 2015-12-16; просмотров: 711;
