Булева алгебра. Основные операции булевой алгебры.

Простые высказывания можно рассматривать как некоторые переменные, которые принимают значение на множестве 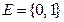(0-ЛОЖЬ, 1-ИСТИНА). Такие переменные называют булевыми переменными.

Определение 7.1. Всякую переменную, которая может принимать одно из двух возможных значений, обозначаемых ноль или единица, назовём булевой переменной.

Определение 7.2. Функция 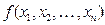, принимающая значение на множестве 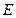, называется булевой функцией.

Совокупность значений булевой функции называют набором. Например: для 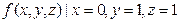набором является .

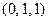Определение 7.3. Булева алгебра есть множество 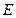, содержащее специальные элементы ноль и единицу, на котором заданы бинарные операции: .

Аксиомы алгебры:

1. Законы коммутативности:

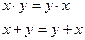
2. Законы дистрибутивности:

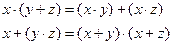
3. Законы тождества (свойства нуля и единицы):

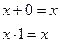
4. Закон исключенного третьего и закон противоречия (законы дополнения):

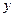Используя аксиомы можно доказать ряд теорем о булевых алгебрах. Для всех элементов и булевой алгебры выполняются следующие соотношения:

1. Законы идемпотентности:

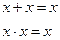
2. Свойства констант:

3. Законы поглощения:

4. Закон инволюции:

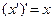
5. Дополнение законов тождества:

6. Законы де Моргана

Каждая аксиома булевой алгебры состоит из пары равенств, которые являются двойственными, в том смысле, что если в одном равенстве заменить сложение на умножение, умножение на сложение, единицу на ноль и ноль на единицу, получим второе равенство. В результате каждая теорема обладает двойственностью, в том смысле, что если в любой теореме булевой алгебры заменить сложение на умножение, умножение на сложение, единицу на ноль и ноль на единицу, снова получим теорему, хотя она может не отличаться от исходной.

Доказательство:

Законы идемпотентности:

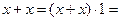
	Свойство констант
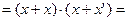
	Закон дополнения
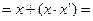
	Закон дистрибутивности
	Закон дополнения
	Закон тождества

Свойства констант:

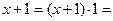
	Закон тождества
	Закон дополнения
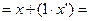
	Закон дистрибутивности
	Закон коммутативности
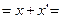
	Закон тождества
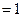
	Закон дополнения

Законы поглощения:

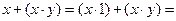
	Закон тождества
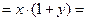
	Закон дистрибутивности
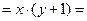
	Закон коммутативности
	Свойство констант
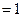
	Закон тождества

Каждая переменная есть формула. Если и 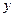– формулы, то формулами являются . Других формул нет.

Приоритет операций: .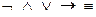

Поскольку одна и та же булева функция может быть представлена различными формулами, возникает вопрос о единственности представления булевой функции, т.е. нахождении такой универсальной формы, чтобы каждая булева функция могла быть представлена в ней. Такими формами являются совершенная конъюнктивная и совершенная дизъюнктивная нормальные формы.

Определение 7.4. Всякая булева формула, построенная с помощью одной только операции дизъюнкция над булевыми переменными или их отрицаниями, называется элементарной дизъюнкцией (дизъюнктом).

Определение 7.5. Всякая булева формула, построенная только с помощью одной операции конъюнкция над булевыми переменными или их отрицаниями, называется элементарной конъюнкцией (конъюнктом).

Теорема 1. Для того, чтобы элементарная дизъюнкция была тождественно равна 1, необходимо и достаточно, чтобы в неё входила некоторая переменная вместе со своим отрицанием.

Теорема 2. Для того, чтобы элементарная конъюнкция была тождественно равна 0, необходимо и достаточно, чтобы в неё входила некоторая переменная вместе со своим отрицанием.

Справедливость первой и второй теорем следует из аксиом законов тождества, закона исключенного третьего и закона противоречия.

Определение 7.6. Булева функция называется конституентой единицы, если она равна единице только на одном наборе своих аргументов.

Определение 7.7. Булева функция называется конституентой нуля, если она равна нулю только на одном наборе своих аргументов.

Пример: среди булевых функций двух аргументов: конъюнкция и стрелка Пирса являются конституентами единицы, а дизъюнкция и штрих Шеффера являются конституентами нуля.

Пусть функция на наборе . Тогда она является конституентой нуля и её можно записать в следующем виде: .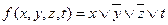

Пусть функция на наборе . Тогда она является конституентой единицы и её можно записать в следующем виде: .

Дизъюнкция элементарных конъюнкций, не содержащая двух одинаковых конъюнкций, называется дизъюнктивной нормальной формой (ДНФ).

ДНФ, все конъюнкции которой есть конституенты единицы, называют совершенной дизъюнктивной нормальной формой (СДНФ).

Конъюнкция элементарных дизъюнкций, не содержащая двух одинаковых дизъюнкций, называется конъюнктивной нормальной формой (КНФ).

КНФ, все дизъюнкции которой есть конституенты единицы, называют совершенной конъюнктивной нормальной формой (СКНФ).