Отношения. Свойства отношений.
Пусть 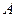 и
и 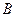 – два множества.
– два множества.
Определение 4.1. Прямым (декартовым) произведением двух множеств 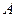 и
и 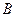 называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит множеству
называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит множеству 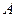 , а второй множеству
, а второй множеству 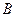 :
:
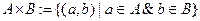 .
.
Определение 4.2. Степенью множества 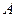 называется его прямое произведение самого на себя. Соответственно:
называется его прямое произведение самого на себя. Соответственно: 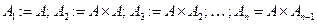 .
.
Теорема: 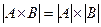 .
.
Доказательство:
Первый компонент упорядоченной пары можно выбрать 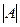 способами, второй –
способами, второй – 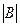 способами (
способами ( 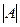 – число элементов множества
– число элементов множества 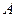 ;
; 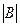 – число элементов множества
– число элементов множества 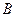 ). Т.о., всего имеется
). Т.о., всего имеется 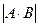 упорядоченных пар.
упорядоченных пар.
Пример: 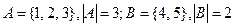 ;
;
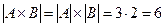 ;
;
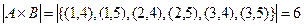 .
.
Определение 4.3. Бинарным отношением 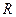 из множества
из множества 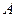 в множество
в множество 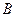 называется подмножество прямого произведения:
называется подмножество прямого произведения: 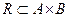 . Для бинарных отношений обычно используется инфиксная форма записи:
. Для бинарных отношений обычно используется инфиксная форма записи: 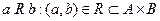 .
.
Если 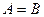 , то говорят, что
, то говорят, что 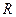 есть отношение на множестве
есть отношение на множестве 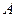 и записывают
и записывают 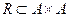 или
или 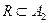 .
.
Т.к. всякое бинарное отношение – множество, то над ним можно проводить следующие операции: объединение, пересечение и разность.
Пусть бинарные отношения 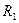 и
и 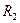 определены на множествах
определены на множествах 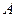 и
и 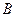 , тогда:
, тогда:
объединение: 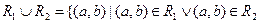 ;
;
пересечение: 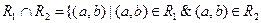 ;
;
разность: 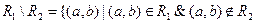 .
.
Обобщением понятия бинарного отношения является понятие 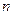 -местного или
-местного или 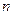 -арного отношения, которое является подмножеством прямого произведения
-арного отношения, которое является подмножеством прямого произведения 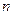 множеств.
множеств.
Определение 4.4. 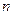 -местным отношением называется любое подмножество множества
-местным отношением называется любое подмножество множества 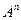 , где
, где 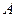 – произвольное множество,
– произвольное множество, 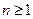 . При
. При 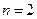 отношение называют бинарным, а при
отношение называют бинарным, а при 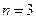 – тернарным:
– тернарным:
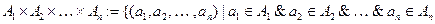 .
.
Пусть 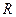 – есть отношение на множествах
– есть отношение на множествах 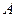 и
и 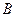 :
: 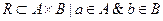 . Введем следующие понятия:
. Введем следующие понятия:
1. обратное отношение: 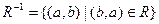 ;
;
2. дополнение отношения: 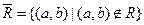 ;
;
3. тождественное отношение: 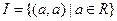 ;
;
4. универсальное отношение: 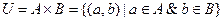 .
.
Пример: Пусть заданы множества 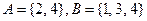 и пусть отношение
и пусть отношение 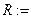 быть в 2 раза меньше.
быть в 2 раза меньше.
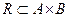 ;
;
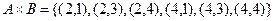 ;
;
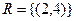 ;
;
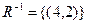 ;
;
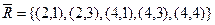 ;
;
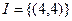 .
.
Если 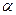 – отношение, заданное на множестве
– отношение, заданное на множестве 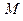 , то обратное отношение
, то обратное отношение 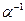 определяется как
определяется как 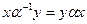 .
.
Отношения 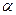 и
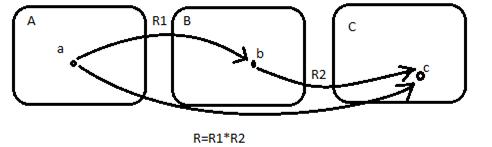
и 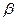 могут образовывать композицию (произведение) отношений, которое само является отношением.
могут образовывать композицию (произведение) отношений, которое само является отношением. 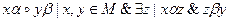 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Свойства соответствий. | | | Схемы и линейные программы. |
Дата добавления: 2015-12-16; просмотров: 720;
