Свойства соответствий.

Основные понятия и правила комбинаторики.

На практике часто встречаются задачи, где необходимо подсчитать число всех возможных способов размещения объектов конечного множества или число всех возможных способов выполнения определенного действия из конечного множества таких действий.

Задачи такого типа называют комбинаторными, а методы их решения – методами комбинаторного анализа. Поскольку комбинаторика имеет дело с конечными множествами, то ее называют теорией конечных множеств.

Определение 2.1. Комбинаторика – раздел дискретной математики, посвященный решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными свойствами.

Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило произведения и правило суммы.

Основное правило комбинаторики (правило произведения):

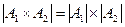
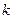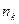Пусть необходимо выполнить последовательно действий. Если первое действие можно выполнить способами, второе – способами, а -е – способами, то все 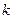действий можно выполнить 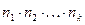способами.

Правило суммы:

Если элемент 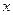может быть выбран 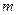способами, а элемент 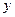другими 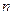способами, то выбор либо 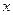, либо 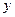может быть выбран 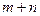способами.

Будем рассматривать задачи, связанные с нахождением числа способов построения кортежей из элементов конечного множества. Простейшими такими кортежами являются: размещения, перестановки и сочетания. Эти задачи образуют часть комбинаторики, называемую перечислительной комбинаторикой или теорией перечислений.

Размещения (arrangement).

Пусть 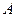– конечное множество, состоящее из 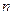элементов .

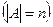Определение 2.2. Кортежи длины 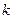, , 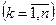состоящие из различных элементов 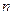-элементного множества 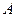(кортежи отличаются один от другого как самими элементами, так и их порядком), называются размещениями из 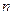элементов множества 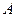по , .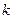

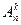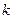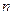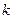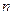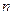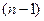Схема выбора состоит в выборе элементов из -элементного множества без возвращений. Тогда необходимо совершить действий, причем первое действие можно совершить способами, -е – способами, 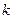-е – 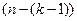способами и т.д. Согласно комбинаторному правилу умножения, получим формулу:

.

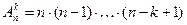Если умножить и разделить полученное выражение на 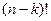, получим:

.

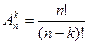Пример:

Дано множество 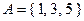. Выпишем все размещения из трех элементов по два:

.

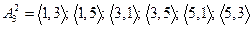Число этих размещений можно найти по формуле:

.

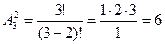Перестановки (permutation).

Пусть 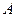– конечное множество из 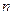элементов.

Определение 2.3. Будем строить из этого множества размещения в виде кортежей длины 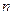. Эти размещения будут отличаться друг от друга только порядком элементов, поскольку в каждом из них встречаются по одному разу все элементы множества 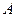. Такие размещения называют перестановками, 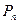. Поскольку 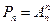, то число перестановок вычисляется по формуле .

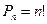Пример:

Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая входит в число только один раз.

Составим следующие тройки: 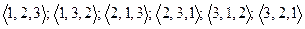– то есть шесть чисел. С помощью введенной формулы можно сразу определить число перестановок, не выписывая их:

.

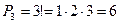Сочетания (combination).

Пусть 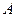– конечное множество из 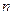элементов.

Определение 2.4. Будем строить упорядоченные множества длины 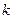, , 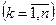не учитывая порядок элементов, т. е. размещения с одними и теми же элементами, расположенными в разном порядке, будем считать равными. Такие размещения называются сочетаниями, .

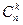Число сочетаний из элементов по 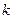меньше числа размещений из 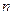элементов по 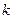в 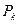раз, т. е.:

.

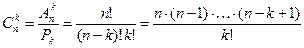Пример:

Какие парные сочетания можно составить из цифр 1, 3, 5 и сколько их?

Выпишем эти сочетания: 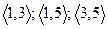, т. е. 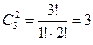или .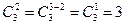

Комбинации элементов с повторениями

Все приведенные формулы справедливы в том случае, когда 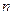элементов множества 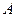различны. Если же некоторые элементы повторяются, то в этом случае рассматриваются комбинации с повторениями,число которых вычисляется по другим формулам.

Размещения с повторениями.

Определение 2.5. Размещениями с повторениями из 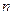элементов по 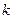называются кортежи длины 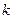, составленные из 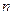-элементного множества 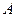. Число этих кортежей обозначают 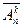. Черта указывает на возможность повторения элементов .

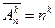Пример:

Сколько пятизначных номеров можно составить из элементов множества ?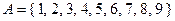

Такими номерами являются кортежи длины 5, составленные из девятиэлементного множества, где схема выбора состоит в выборе 5 элементов из девятиэлементного множества с возвращением, т. е. для каждого из пяти элементов есть девять способов выбора: .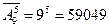

Перестановки с повторениями.

Определение 2.6. Перестановкой с повторениями состава 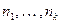из элементов 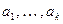называют любой кортеж длины 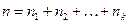, в который 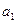входит 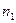раз, 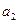входит 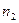раз, 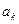– 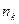раз. Число таких перестановок:

.

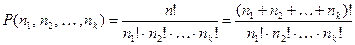Пример:

Сколько слов можно получить, переставляя буквы в слове "МАТЕМАТИКА"?

В слове "МАТЕМАТИКА" 2 буквы М, 3 буквы А, 2 буквы Т, 1 буква Е, 1 буква И и 1 буква К. Число слов будет равно:

.

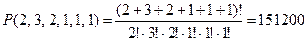Сочетания с повторениями.

Определение 2.7. Пусть имеются предметы 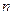видов и из них составляется набор, содержащий 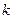элементов, т. е. различными исходами будут всевозможные наборы длины 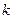, отличающиеся составом, и при этом отдельные наборы могут содержать повторяющиеся элементы. Такие наборы называются сочетаниями с повторениями, а их общее число определяется формулой:

.

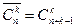Пример:

Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта?

Искомое число равно .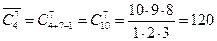

Соответствия.

Пусть 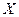и 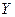– произвольные множества.

Определение 2.8. Соответствием 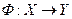называется произвольное подмножество 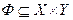. В частном случае, когда каждый элемент 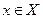входит не более, чем в одну пару 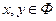, получается обычное однозначное отображение из 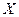в 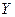, или функция. Таким образом, понятие соответствия обобщает понятие функции.

Пример:

Пусть .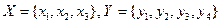

Декартово произведение 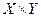показано на рис.1 в виде прямоугольной таблицы, а элементы 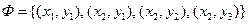представлены заполненными точками.

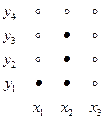
рис.1. Пример соответствия

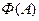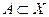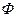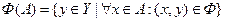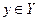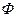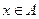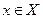Определение 2.9. Образом множества при соответствии называется множество точек , входящих в в паре с некоторым . Для образ одноточечного множества будем также обозначать .

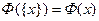Определение 2.10. Обратным к 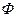соответствием 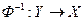называется подмножество 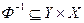, определяемое следующим образом:

.

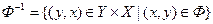Пример:

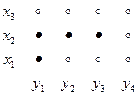
рис.2. Пример обратного соответствия

Образ 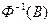множества 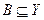при соответствии 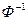называют также прообразом 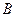при соответствии 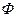. Для обозначения прообразов одноточечных множеств 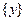используется то же соглашение, что и для образов 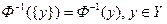. Понятие соответствия оказывается особенно удачным в том смысле, что обратное соответствие всегда существует, и .

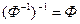В общем случае, рассматриваются множества, элементы которых имеют различную природу. Например: отношение 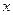родился в году 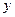является подмножеством декартова произведения множества людей и множества лет и ставит в соответствие каждому человеку его год рождения. Для исключения подобных отношений вводятся понятия соответствия, отображения, функции.

Свойства соответствий.

Соответствие 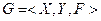называется функциональным, если образ любого элемента 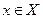, содержит не более одного элемента, то есть график такого соответствия не содержит пар с одинаковыми первыми и разными вторыми элементами.

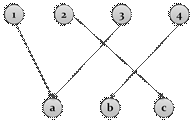
рис.3. Функциональное соответствие

В противном случае соответствие является нефункциональным, т.е. если образ любого элемента , содержит более одного элемента.

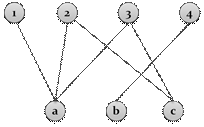
рис.4. Нефункциональное соответствие

В случае, если каждому элементу соответствует более одного элемента из 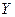, соответствие называется антифункциональным.

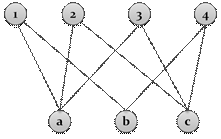
рис.5. Антифункциональное соответствие

Соответствие 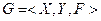называется инъективным, если прообраз 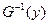любого элемента 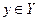содержит не более одного элемента из 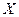, т. е. график такого соответствия не содержит пар с одинаковыми вторыми и разными первыми элементами.

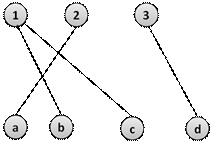
рис.6. Инъективное соответствие

Соответствие 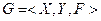называется неинъективным, если прообраз 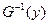любого элемента 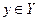содержит более одного элемента из .

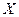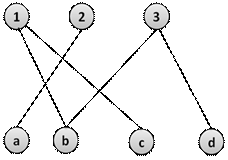
рис.7. Неинъективное соответствие

Соответствие 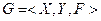называется антиинъективным, если, каждый прообраз 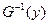любого элемента 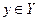содержит более одного элемента из .

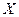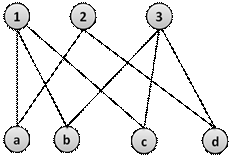
рис.8. Антиинъективное соответствие

Соответствие 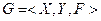называется всюду определенным, если для каждого 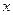, его образ 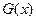не равен пустому множеству, то есть в графике такого соответствия из любой вершины 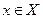выходит по крайней мере одна стрелка.

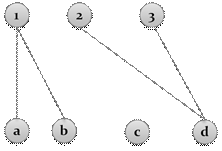
рис.9. Всюду определенное соответствие

Соответствие 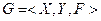называется сюръектиеным, если для любого 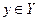его прообраз 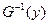не равен пустому множеству, то есть в графике такого соответствия в любую вершину 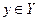входит хотя бы одна стрелка.

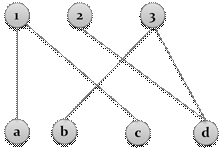
рис.10. Сюръективное соответствие

Соответствие называется биективным или взаимооднозначным, если оно функционально, инъективно, всюду определено и сюръективно.

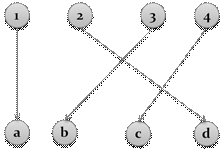
рис.11. Биективное соответствие