Нахождение относительных сезонных колебаний
| Год | Номер месяца | Yi | 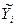 (Тренд) (Тренд)
| Относительное сезонное колебание |
| 34,8034 | 0,6034 | |||
| 35,0506 | 0,7418 | |||
| 35,2978 | 0,8216 | |||
| 35,5450 | 0,9003 | |||
| 35,7922 | 1,0617 | |||
| 36,0394 | 1,0821 | |||
| 36,2866 | 1,2126 | |||
| 36,5338 | 1,3412 | |||
| 36,7811 | 1,2506 | |||
| 37,0283 | 1,1343 | |||
| 37,2755 | 1,2341 | |||
| 37,5227 | 1,2526 | |||
| 37,7699 | 0,6884 | |||
| 38,0171 | 0,8417 | |||
| 38,2643 | 0,8102 | |||
| 38,5115 | 0,6492 | |||
| 38,7587 | 1,0062 | |||
| 39,0060 | 1,1024 | |||
| 39,2532 | 1,1209 | |||
| 39,5004 | 1,2405 | |||
| 39,7476 | 1,3334 | |||
| 39,9948 | 1,2502 | |||
| 40,2420 | 1,2425 | |||
| 40,4892 | 1,2102 | |||
| 40,7364 | 0,6873 | |||
| 40,9837 | 0,7320 | |||
| 41,2309 | 0,7034 | |||
| 41,4781 | 0,7474 | |||
| 41,7253 | 0,7430 | |||
| 41,9725 | 0,9768 | |||
| 42,2197 | 0,9474 | |||
| 42,4669 | 1,1067 | |||
| 42,7141 | 1,1472 | |||
| 42,9613 | 1,0707 |
Рассмотрим способ вычисления относительной циклической составляющей путем нахождения сезонной волны.
Из выражения (2) при условии (3) получаем
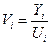 (4)
(4)
Согласно полученному выражению (4) рассчитаем относительные значения циклических колебаний на всем временном интервале известных значений (Таблица 3).
И найдем сезонную волну как средние относительные значения циклических колебаний для выделенного периода (года), по формуле:
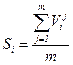 (5)
(5)
Где: m – число выделенных периодов.
И заполним таблицу (Таблица 4).
Таблица 4
Сезонная волна
| Номер месяца | Относительное суммарное сезонное колебание | Относительная сезонная волна |
| 1,979 | 0,6597 | |
| 2,316 | 0,7718 | |
| 2,335 | 0,7784 | |
| 2,297 | 0,7656 | |
| 2,811 | 0,9370 | |
| 3,161 | 1,0538 | |
| 3,281 | 1,0936 | |
| 3,688 | 1,2295 | |
| 3,731 | 1,2437 | |
| 3,455 | 1,1517 | |
| 2,477 | 1,2383 | |
| 2,463 | 1,2314 |
Используем ряд Фурье в качестве аналитической модели сезонности. В этом виде уравнение ряда Фурье запишется следующим образом:
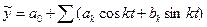 (6)
(6)
В этом уравнении величина 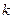 определяет номер гармоники ряда Фурье. От числа учтенных гармоник зависит степень точности данной аналитической модели. Обычно используют от 1 до 4 гармоник в зависимости от необходимой точности и формы сезонной или циклической составляющей. Для отыскания параметров уравнения используется метод наименьших квадратов.
определяет номер гармоники ряда Фурье. От числа учтенных гармоник зависит степень точности данной аналитической модели. Обычно используют от 1 до 4 гармоник в зависимости от необходимой точности и формы сезонной или циклической составляющей. Для отыскания параметров уравнения используется метод наименьших квадратов.
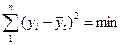 (7)
(7)
Найдя частные производные этой функции и приравняв их нулю, получим систему нормальных уравнений, решение которой дает следующие формулы для вычисления параметров:
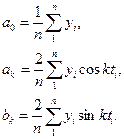 (8)
(8)
Как видно из формул, параметры уравнений зависят от значений у и связанных с ними последовательных значений cos(kti) и sin (kti.).
Для изучения сезонных колебаний на протяжении выбранного периода (года) необходимо взять n = 12 (по числу месяцев в году). Тогда, представляя периоды как части длины окружности, ряд динамики можно записать в следующем виде:
Таблица 4
| Период | 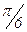
| 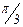
| 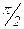
| 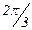
| 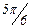
| 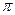
| 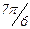
| 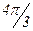
| 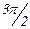
| 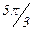
| 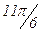
| |
| Уровень | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | y11 |
Величины периодов 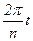 получаются следующим способом:
получаются следующим способом:
При 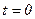
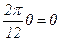 , при
, при 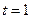
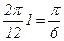 и т.д.
и т.д.
При вычислении надо иметь в виду, что в четырех квадрантах от 0 до 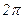 косинусы и синусы четыре раза принимают одни и те же абсолютные значения, а именно: 0; 0,5; 0,866; 1, взятые со знаком «плюс» или «минус». Вычисления синусов и косинусов разных гармоник приведены в табл. 5.
косинусы и синусы четыре раза принимают одни и те же абсолютные значения, а именно: 0; 0,5; 0,866; 1, взятые со знаком «плюс» или «минус». Вычисления синусов и косинусов разных гармоник приведены в табл. 5.
Таблица 5
| t | cos t | cos 2t | cos 3t | cos 4t | sin t | sin 2t | sin 3t | sin 4t |
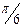
| 0,866 | 0,5 | -0,5 | 0,5 | 0,866 | 0,866 | ||
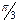
| 0,5 | -0,5 | -1 | -0,5 | 0,866 | 0,866 | -0,866 | |

| -1 | |||||||
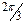
| -0,5 | -0,5 | -0,5 | 0,866 | -0,866 | 0,866 | ||
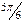
| -0,866 | 0,5 | -0,5 | 0,5 | -0,866 | -0,866 | ||
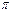
| -1 | -1 | ||||||
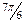
| -0,866 | 0,5 | -0,5 | -0,5 | 0,866 | -1 | 0.866 | |
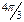
| -0,5 | -0,5 | -0,5 | -0,866 | 0,866 | -0,866 | ||
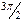
| -1 | -1 | ||||||

| 0,5 | -0,5 | -1 | -0,5 | -0,866 | -0,866 | 0,866 | |

| 0,866 | 0,5 | -0,5 | -0,5 | -0,866 | -1 | -0,866 |
Вычисление синусов и косинусов годовой динамике t обозначает номер месяца. Для определения параметров ак и bк находят соответствующие уравнения для гармоники. Для первой гармоники, т.е. для 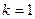 , уравнение примет вид:
, уравнение примет вид:
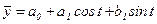 (9)
(9)
в котором параметры a0, a1 и b1, будут найдены из соотношений:
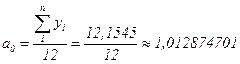
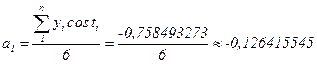
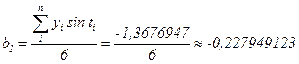
Уравнение модели с учетом только первой гармоники (рис. 9) будет иметь следующий вид:
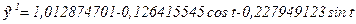
Далее построим модель сезонной волны, применив первую и вторую гармоники ряда Фурье (табл. 6).
Таблица 6
| Месяц | t | Относительное сезонное колебание | у cos t | у sin t | y1 | у cos 2t | у sin 2t | y2 |
| Январь | 0,6597 | 0,659704703 | 0,886459156 | 0,659704703 | 0,9930 | |||
| Февраль | 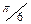
| 0,7718 | 0,66841076 | 0,38591845 | 0,789424278 | 0,385918453 | 0,66841076 | 0,9483 |
| Март | 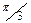
| 0,7784 | 0,389182007 | 0,67406324 | 0,752262988 | -0,38918201 | 0,674063236 | 0,9682 |
| Апрель | 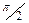
| 0,7656 | 0,76560211 | 0,784925579 | -0,76560211 | 1,0328 | ||
| Май | 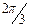
| 0,9370 | -0,468477138 | 0,8114024 | 0,878678534 | -0,46847714 | -0,8114024 | 1,0774 |
| Июнь | 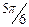
| 1,0538 | -0,912583347 | 0,5268957 | 1,008376002 | 0,526895697 | -0,91258335 | 1,0575 |
| Июль | 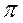
| 1,0936 | -1,093640386 | 1,139290247 | 1,093640386 | 0,9930 | ||
| Август | 
| 1,2295 | -1,064735531 | -0,6147434 | 1,236325125 | 0,614743378 | 1,064735531 | 0,9483 |
| Сентябрь | 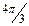
| 1,2437 | -0,62186987 | -1,0770786 | 1,273486414 | -0,62186987 | 1,077078615 | 0,9682 |
| Октябрь | 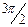
| 1,1517 | -1,1517203 | 1,240823824 | -1,15172032 | 1,0328 | ||
| Ноябрь | 
| 1,2383 | 0,619134436 | -1,0723408 | 1,147070869 | -0,61913444 | -1,07234084 | 1,0774 |
| Декабрь | 
| 1,2314 | 1,066381093 | -0,6156935 | 1,0173734 | 0,615693472 | -1,06638109 | 1,0575 |
| Итого | 12,1545 | -0,758493273 | -1,3676947 | 12,15449642 | -0,11938979 | -0,37841955 | 12,1545 |
Находим вторую гармонику Фурье:
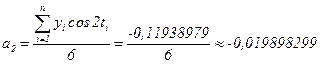 ,
,
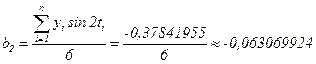
Уравнение модели с двумя гармониками будет иметь следующий вид:
 Таким образом, можно сказать, что мы нашли аналитическое выражение циклической (сезонной) составляющей Vt.
Таким образом, можно сказать, что мы нашли аналитическое выражение циклической (сезонной) составляющей Vt.
Итак, построим общую модель ряда 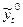 представляющую произведение составляющих U и V без случайной компоненты, а именно:
представляющую произведение составляющих U и V без случайной компоненты, а именно:
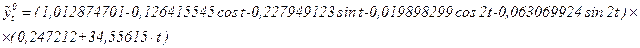
Полученное уравнение — модель ряда yt, для которого известны составляющие Ut , Vt. Случайную составляющую Еt, можно получить следующим образом:
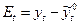
Поскольку 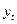 , и
, и  , — известные величины, то найти Еt, нетрудно. Модель, учитывающая составляющие Ut, Vt, Et для данного ряда, может быть записана так:
, — известные величины, то найти Еt, нетрудно. Модель, учитывающая составляющие Ut, Vt, Et для данного ряда, может быть записана так:
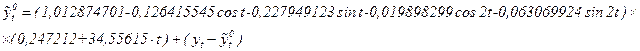
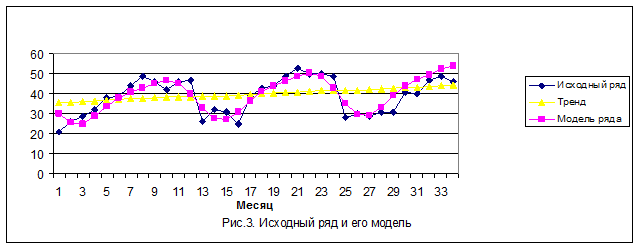
График исходного динамического ряда, тренда и общей модели ряда у0 представлен на рис.3.
Исследуем качество модели. Так как методика оценки качества аналогична методике оценки качества линейной модели, подробно излагать ее не будем, а приведем лишь основные расчеты.
1. Проверка случайностей уровней на основе критерия поворотных точек.
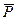 = 23 — число поворотных точек (табл.7).
= 23 — число поворотных точек (табл.7).
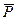 >Р- целая часть от
>Р- целая часть от 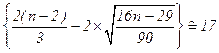
где п — число членов ряда.
Следовательно, 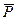 >Р, так как 23 > 17, и свойство случайностей выполняется.
>Р, так как 23 > 17, и свойство случайностей выполняется.
Таблица7
Дата добавления: 2015-12-16; просмотров: 900;
